nLab Poincaré–Hopf theorem
Context
Topology
topology (point-set topology, point-free topology)
see also differential topology, algebraic topology, functional analysis and topological homotopy theory
Basic concepts
-
fiber space, space attachment
Extra stuff, structure, properties
-
Kolmogorov space, Hausdorff space, regular space, normal space
-
sequentially compact, countably compact, locally compact, sigma-compact, paracompact, countably paracompact, strongly compact
Examples
Basic statements
-
closed subspaces of compact Hausdorff spaces are equivalently compact subspaces
-
open subspaces of compact Hausdorff spaces are locally compact
-
compact spaces equivalently have converging subnet of every net
-
continuous metric space valued function on compact metric space is uniformly continuous
-
paracompact Hausdorff spaces equivalently admit subordinate partitions of unity
-
injective proper maps to locally compact spaces are equivalently the closed embeddings
-
locally compact and second-countable spaces are sigma-compact
Theorems
Analysis Theorems
Differential geometry
synthetic differential geometry
Introductions
from point-set topology to differentiable manifolds
geometry of physics: coordinate systems, smooth spaces, manifolds, smooth homotopy types, supergeometry
Differentials
Tangency
The magic algebraic facts
Theorems
Axiomatics
Models
differential equations, variational calculus
Chern-Weil theory, ∞-Chern-Weil theory
Cartan geometry (super, higher)
Contents
Idea
The Poincaré–Hopf theorem says that for any vector field with a finite set of isolated vanishing points on an orientable compact differential manifold , the sum over the of the degrees of the vector in the vicinity of these points, regarded as cohomotopy classes
and called the Poincaré–Hopf index of at
is given by the Euler characteristic, hence by the value of the Euler class on the tangent bundle:
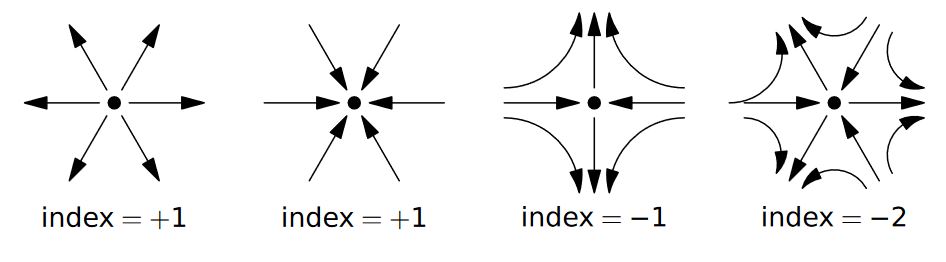
In particular, the existence of a nowhere vanishing vector field (for which the above sum is empty) implies that the Euler characteristic vanishes.
The converse also holds: If the Euler characteristic of a closed manifold vanishes, then a nowhere vanishing vector field exists (e.g. MO:a/47553/58526).
Also: Given any connected closed manifold, the complement of any positive number of disjoint open balls carries a nowhere vanishing vector field (namely: choose any vector field with isolated zeros on the original manifold and then deform continuously to push all these zeros into inside the open balls). Smoothly scaling this vector field to zero towards the centers of these open balls gives a vector field on the original manifold which may be used in the PH-theorem.
Related concepts
References
Named after Henri Poincaré and Heinz Hopf.
Textbook accounts:
-
Raoul Bott, Loring Tu, Chapter 11 of Differential Forms in Algebraic Topology, Graduate Texts in Mathematics 82, Springer 1982 (doi:10.1007/BFb0063500)
-
B. A. Dubrovin, S. P. Novikov, A. T. Fomenko, section 15.2 of Modern Geometry — Methods and Applications: Part II: The Geometry and Topology of Manifolds, Graduate Texts in Mathematics 104, Springer-Verlag New York, 1985 (doi:10.1007/978-1-4612-1100-6)
-
John Milnor, Chapter 6 of: Topology from the differential viewpoint, Princeton University Press, 1997. (ISBN:9780691048338, pdf)
-
Gerard Walschap, chapter 6.7 of Metric Structures in Differential Geometry, Graduate Texts in Mathematics, Springer 2004
Review:
-
Alex Wright, Kael Dixon, The Poincaré–Hopf theorem (pdf)
-
Ariel Hafftka, Differential topology and the Poincaré–Hopf theorem (pdf)
See also:
- Wikipedia, Poincaré–Hopf theorem
Discussion in a broader perspective of K-theory and index theorems:
A comment on the version for complex vector fields is in
- Howard Jacobowitz, Non-vanishing complex vector fields and the Euler characteristic (arXiv:0901.0893)
Generalization to orbifolds:
- Christopher Seaton, Two Gauss–Bonnet and Poincaré–Hopf theorems for orbifolds with boundary, Differential Geometry and its Applications Volume 26, Issue 1, February 2008, Pages 42-51 (doi:10.1016/j.difgeo.2007.11.002)
Last revised on March 3, 2021 at 07:07:05. See the history of this page for a list of all contributions to it.