nLab first stable homotopy group of spheres

Idea

The first stable homotopy group of spheres (the first stable stem) is the cyclic group of order 2:

(1)$$\array{ \pi_1^s &\simeq& \mathbb{Z}/2 \\ [h_{\mathbb{C}}] &\leftrightarrow& [1] }$$

where the generator $[1] \in \mathbb{Z}/2$ is represented by the complex Hopf fibration $S^3 \overset{h_{\mathbb{C}}}{\longrightarrow} S^2$.

from SS21

Properties

As the first framed bordism group

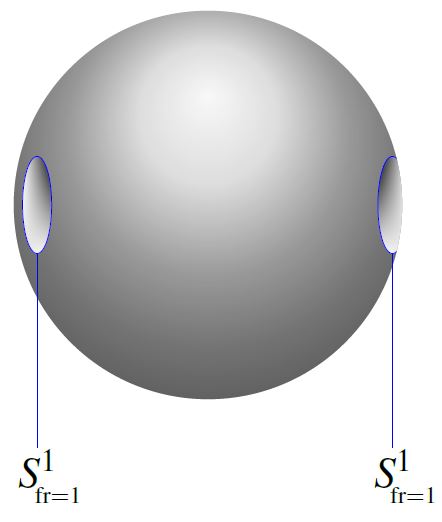
Under the Pontrjagin-Thom isomorphism, identifying the stable homotopy groups of spheres with the bordism ring $\Omega^{fr}_\bullet$ of stably framed manifolds (see at MFr), the generator (1) is represented by the 1-sphere (with its left-invariant framing induced from the identification with the Lie group U(1))

$$\array{ \pi_1^s & \simeq & \Omega_1^{fr} \\ [h_{\mathbb{C}}] & \leftrightarrow & [S^1_{fr=1}] \,. }$$

Moreover, the relation $2 \cdot [S^1_{Lie}] \,\simeq\, 0$ is represented by the bordism which is the complement of 2 open balls inside the 2-sphere.

Related concepts

• complex Hopf fibration

• second stable homotopy group of spheres

• third stable homotopy group of spheres

• homotopy groups of spheres in HoTT

References

The original computation via Pontryagin's theorem in cobordism theory:

• Lev Pontrjagin, Classification of continuous maps of a complex into a sphere, Communication I, Doklady Akademii Nauk SSSR 19(3) (1938), 147-149

with a more comprehensive account in:

• Lev Pontrjagin, Section 14 of: Smooth manifolds and their applications in homotopy theory, Trudy Mat. Inst. im Steklov, No 45, Izdat. Akad. Nauk. USSR, Moscow, 1955 (AMS Translation Series 2, Vol. 11, 1959) (doi:10.1142/9789812772107_0001)

See also:

• Mehmet Kirdar, On the First, the Second and the Third Stems of the Stable Homotopy Groups of Spheres [arXiv:2107.06103]

Review:

• Daniel Freed, Karen Uhlenbeck, Appendix B of: Instantons and Four-Manifolds, Mathematical Sciences Research Institute Publications, Springer 1991 (doi:10.1007/978-1-4613-9703-8)

• Guozhen Wang, Zhouli Xu, Section 2.3 of: A survey of computations of homotopy groups of Spheres and Cobordisms, 2010 (pdf)

• Andrew Putman, Section 5 of: Homotopy groups of spheres and low-dimensional topology (pdf, pdf)

Discussion in homotopy type theory:

• Guillaume Brunerie: On the homotopy groups of spheres in homotopy type theory $[$arxiv:1606.05916$]$

• Axel Ljungström, The Brunerie Number Is -2 (June 2022) $[$blog entry$]$