nLab function application to identifications

Idea

The type-theoretic version of the fact that in set theory functions preserve equality between elements in sets.

Definition

Basic definition

In dependent type theory, given types $A$ and $B$ and a function $x \colon A \vdash f(x) \colon B$, there is induced a dependent function between the corresponding identity types

$$a \colon A ,\,\; b\colon A ,\,\; p \,\colon\, a =_A b \;\;\;\vdash\;\;\; \mathrm{ap}_f(a, b)(p) \;\colon\; f(a) =_B f(b)$$

defined by Id-induction from

$$ap_f\big(refl_a\big) \,\equiv\, refl_{f(a)}$$

and called the application or action of $f$ to/on identities/identifications/equalities/paths [e.g. UFP (2013, p. 69), Rijke (2022, §5.3)].

By repeated Id-induction it readily follows, stagewise (e.g. UFP13, Lem 2.2.1), that $ap_f$ respects the concatenation, and the inversion of identifications, up to coherent higher-order identifications, hence that it acts as an $\infty$-functor on the $\infty$-groupoid-structure on homotopy types :

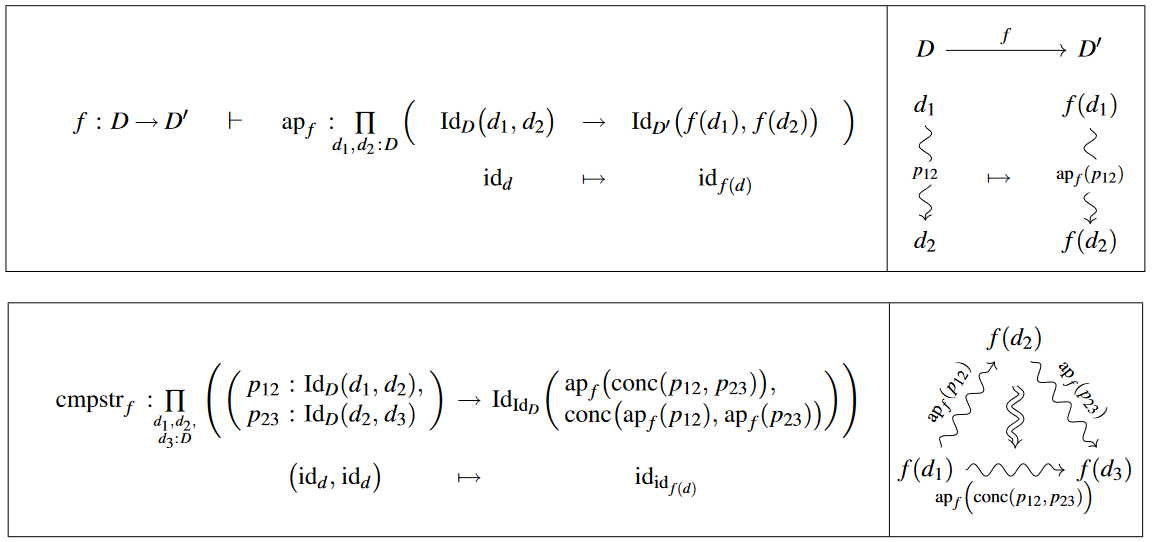
As the non-dependent version of the dependent function application to identifications

The function application to identifications is a special case of the dependent function application to identifications for which the type family $x:A \vdash B$ is a constant type family, and thus the dependent identity type $f(a) =_B^p f(b)$ doesn’t depend on the path $p:a =_A b$ and is thus a normal identity type $f(a) =_B f(b)$.

Inductive definition

If the function application to identifications is inductively defined, then it comes with rules saying that the following judgment can be formed

$$a:A \vdash \mathrm{ap}_{f}(a, a)(\mathrm{refl}_{A}(a)) \equiv \mathrm{refl}_{B}(f(a)):\Omega(B, f(a))$$

where $\Omega(A, a)$ is the loop space type $a =_A a$ of $A$ at $a:A$.

Binary function applications to identifications

Given types $A$, $B$, and $C$ and a binary function $x:A, y:B \vdash f(x, y):C$, there is a dependent function

$$a:A, a':A, b:B, b':B, p:a =_A a', q:b =_B b' \vdash \mathrm{apbinary}_f(a, a', b, b')(p, q):f(a, b) =_C f(a', b')$$

called the binary function application to identifications or binary action on identifications (Rijke (2022), §19.5), inductively defined by

$$a:A, b:B \vdash \mathrm{apbinary}_{f}(a, a, b, b)(\mathrm{refl}_{A}(a), \mathrm{refl}_{B}(b)) \equiv \mathrm{refl}_{C}(f(a, b)):\Omega(C, f(a, b))$$

where $\Omega(A, a)$ is the loop space type $a =_A a$ of $A$ at $a:A$.

Binary function applications to identifications are used in proving product extensionality for product types, as well as defining multiplication on the integers $\mathrm{apbinary}_{\mu}:\mathbb{Z} \times \mathbb{Z} \to \mathbb{Z}$ from multiplication on the circle type $\mu:S^1 \times S^1 \to S^1$ when the integers are defined as the loop space type of the element $\mathrm{base}:S^1$, $\mathbb{Z} \coloneqq \Omega(S^1, \mathrm{base})$.

Finitary function application to identifications

Let $n$ be a natural number, let $A$ be a family of types indexed by the finite type with $n$ elements $\mathrm{Fin}(n)$, and let $B$ be a type. Then given a function

$$n:\mathbb{N}, x:\left(\prod_{i:\mathrm{Fin}(n)} A(i)\right) \vdash f(x):B$$

there is a dependent function

$$n:\mathbb{N}, a:\prod_{i:\mathrm{Fin}(n)} A(i), b:\prod_{i:\mathrm{Fin}(n)} A(i) \vdash \mathrm{ap}_f(n)(a, b):\left(\prod_{i:\mathrm{Fin}(n)} a(i) =_{A(i)} b(i)\right) \to f(a) =_{B} f(b)$$

See also

• dependent function application to identifications

• identification

• identification type

References

• Univalent Foundations Project, §2.2 in: Homotopy Type Theory – Univalent Foundations of Mathematics (2013) [web, pdf]

• Egbert Rijke, §5.3 in: Introduction to Homotopy Type Theory, Cambridge Studies in Advanced Mathematics, Cambridge University Press (arXiv:2212.11082)