nLab graph complex
Context
Cohomology
Special and general types
-
group cohomology, nonabelian group cohomology, Lie group cohomology
-
-
cohomology with constant coefficients / with a local system of coefficients
Special notions
Variants
-
differential cohomology
Extra structure
Operations
Theorems
Contents
- Idea
- Definition
- Overview
- 1) Graph complexes modelling configuration spaces of points
- 2) Graph complexes modelling spaces of knots
- Properties
- Cohomology of configuration spaces via Feynman diagrams
- Cohomology of knot space / higher Vassiliev invariants
- Cohomology of knot graph complex is weight systems on chord diagrams
- Further applications
- Related concepts
- References
Idea
A graph complex is a certain cochain complex spanned by equivalence classes of certain labeled directed graphs, whose differential encodes the operation of contracting away edges in a graph.
Two similar but different classes of examples are usually referred to by default as just “the graph complex”, going back to hints in Kontsevich 92, P. 11-12, Kontsevich 93, 5:
Given a smooth manifold , often taken to be Euclidean space , there is
-
a graph complex model for the real cohomology of the unlabeled ordered configuration space of points in
-
a graph complex model for the real cohomology of the space of knots in .
In both cases, the graphs are interpreted as Feynman diagrams for Chern-Simons theory and the map which identifies these with cocycles in real cohomology of either the (unlabeled & ordered) configuration space of points or the space of knots is given by sending a Feynman diagram to its Feynman amplitude. In the first case this is an n-point function, regarded as a differential form on the configuration space of -points, while in the second case this is a vacuum amplitude depending on the isotopy class of the Wilson loop encoded by the knot – a Vassiliev knot invariant.
Beware that these graph complex models differ only in very small technical detail as the manifold varies and the choice between models for configuration space of points or spaces of knots is made (see the Overview of definitions below), and yet these small details completely change the cohomological nature of the resulting graph complexes; a point not often made manifest when any given author discusses “the graph complex”.
Model for ordered configuration spaces of points
The graph complex model for unlabeled & ordered configuration spaces of points was originally sketched in Kontsevich 92 (p. 11-12) and worked out in detail in Lambrechts-Volić 14 for a Euclidean space. Other authors have claimed generalization to a closed manifold (Campos-Willwacher 16) possibly with boundary (Campos-Idrissi-Lambrechts-Willwacher 18).
Here we denote this version of the graph complex by “”, in contrast to “” for the other model, discussed further below.

This graph complex is spanned by finite directed graphs with linearly ordered internal and external vertices, subject to a sign rule reflecting the orientation of edges. The differential sends any graph to a signed sum of graphs obtained by contracting one of the edges with at least one internal vertex.
Under ordered disjoint union of edges and internal vertices this cochain complex becomes a differential graded-commutative algebra
As such, this is quasi-isomorphic to the semi-algebraic de Rham algebra
of the Fulton-MacPherson compactification of the configuration space of points for points in -dimensional Euclidean space.
The chain map which exhibits this quasi-isomorphism is given by regarding a graph as a Feynman diagram for Chern-Simons theory on and sending it to its corresponding Feynman amplitude, namely to the configuration space-integral of the wedge product of Chern-Simons propagators associated to the edges, regarding Feynman amplitudes as differential forms on configuration spaces of points:
This means that for each edge in a graph a Chern-Simons propagator is assigned, and for each of internal vertices the wedge product of its adjacent Chern-Simons propagators is fiber integrated along the canonical fibration of configuration spaces of points:
just as befits the definition of a Feynman amplitude when regarding them as differential forms on configuration spaces of points.
Model for spaces of knots
The graph complex model for spaces of knots was originally sketched in Kontsevich 93, Section 5 and worked out in Cattaneo, Cotta-Ramusino, Longoni 02, 05, see also Bar-Natan 91.
Here we denote this version of the graph complex by “”, in contrast to “” for the other model, discussed above.
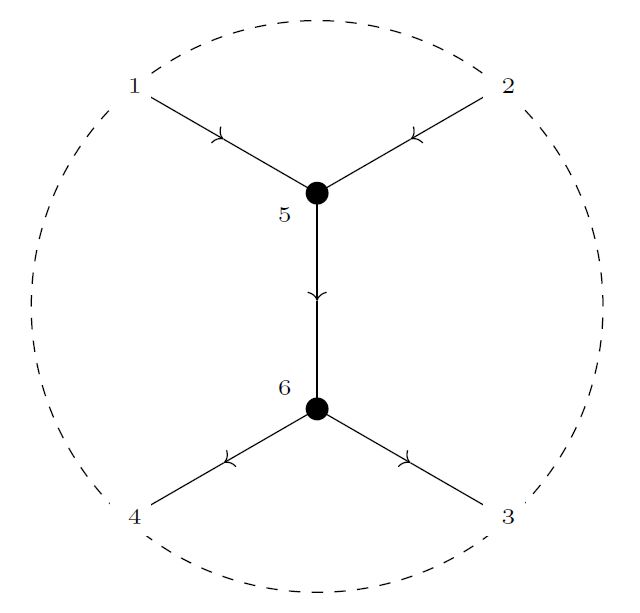
The explicit definition is almost exactly the same as that of the model for configuration spaces of points above, except that the external vertices here have a degree -1 instead of 0, and that the differential sees contractible edges between consecutive external vertices, often called arcs, shown by dashed lines on the right.
Together these two innocent modifications make the graphs now represent vacuum Feynman diagrams for Chern-Simons theory in the presence of a Wilson loop, with the external vertices now attached to this knot (corresponding to the dashed line shown on the right):
This yields higher Vassiliev knot invariants, a good review is in Volić 13. It is a conjecture (Volić 13, Conjecture 4.8) that this map, too, is a quasi-isomorphism.
Model for other spaces
There are yet other, inequivalent, graph complexes. Notably there is a type of graph complex whose (co)homology in degree 0 is the Lie algebra of the Grothendieck-Teichmüller group (Willwacher 10, Dolgushev-Rogers 12), and this is neither of the above two cases. (…)
Definition
Overview
There are two different classes of (Kontsevich-) graph complexes, modelling the real cohomology of, respectively,
| configuration space | graph complex | |||
|---|---|---|---|---|
| configuration spaces of points | (1) | |||
| spaces of knots | (2) |
Despite their very deifferent cohomological nature, the explicit definitions of these two kinds of graph complexes are mostly identical, except for some small but crucial difference in the definition of degrees and labels of edges (see below).
In addition, the definition of the graph complex model for configuration spaces of points depends on a choice of smooth manifold , possibly with boundary, namely such that the graph complex provides a model for the cohomology of the configuration space of points in
The configuration spaces of points are naturally filtered by subspaces of a fixed number of points. In the graph complexes this correpsonds to graphs with a fixed number of external vertices:
The full graph complexes/configuration spaces are just the direct sum/union of those for fixed number of external vertices/points, hence one may focus attention on the latter.
The precise form of these relations is the content of the theorems discussed below. Before stating this in detail, we make some general remarks on how the situation depends on :
Beware that the graphs themselves are not going to carry an embedding into the manifold , they are just abstract graphs. But the construction of the above correspondence to the cohomology of the configuration space of points is given by associating with a graph the corresponding correlator in a Chern-Simons perturbative quantum field theory on the space .
As a consequence, the dependence of the graph complexes themselves on is mild:
In particular, in the case that is a Euclidean space, the corresponding graph complexes depend essentially only on whether the dimension is even or odd. Concretely, the degree of a graph in the graded vector space is
hence each edge contributes a degree and each internal vertex a degree . As a consequence, due to the sign rule in the graded-commutative algebra structure on we have the following parities
| edges | internal vertices | |
|---|---|---|
| even | odd | even |
| odd | even | odd |
Up to an absolute even change of grading, the graph complexes depend only on these parities, hence depend only on whether is even or odd.
Finally, beware that many authors consider the case where by default, and don’t mention a dependence on a choice of manifold, but just on a natural number . This natural number is then often denoted “” or “”.
For instance:
-
the “graph complex with anti-symmetric set of edges” of Bar-Natan & McKay, Def. 3.3 is denoted in Willwacher 10 and is our ;
-
similarly in Koroshkin-Willwacher-Živković 14 is our .
(While the cohomology of – being equivalent to that of – is trivial, these authors consider further filtrations which have non-trivial cohomology in filtration stages, see Bar-Natan & McKay, Def. 3.6).
1) Graph complexes modelling configuration spaces of points
We discuss graph complexes modelling the real cohomology of configuration spaces of points .
For the case of these were originally hinted at in Kontsevich 92 (p. 11-12) and discussed in detail in Lambrechts-Volić 14.
We state the definition of the graph complexes (as motivated above, see Def. below) associated with Euclidean space of dimension 3, following Lambrechts-Volić 14, Section 6.
Graphs
Definition
(graphs)
In the following, by a graph we mean specifically:
-
a decomposition of the finite set of vertices as a disjoint union
of “external” and “internal” vertices.
-
a linear order on , such that .
Hence both and are linear orders, and
is their ordered disjoint union.
An isomorphism of such graphs is a pair of bijections between sets of edges and vertices
which respects all structure, hence the source and target maps, the decomposition into external and internal vertices, and the linear order.
(Lambrechts-Volić 14, Def. 6.1)
We write for the cardinality of the sets of vertices, etc.
Remark
(denotation for linear order on vertices)
The linear order on the vertices in Def. is equivalently a choice of bijection of with the set of the first natural numbers
With this understood, we may depict graphs as as diagrams with oriented edges and numbered vertices.
Definition
(degree of a graph)
Given a graph
according to Def. , its degree is the natural number
hence the sum of 2 for each edge and of -3 for each internal vertex.
(Lambrechts-Volić 14, Def. 6.6)
If we also agree to
-
denote internal vertices by a bullet;
-
denote external vertices by… no denotation (as usual for Feynman diagrams!)
then the ingredients of these graphs are as shown in the following figure:

The following shows some very simple examples of graphs, depicted this way:
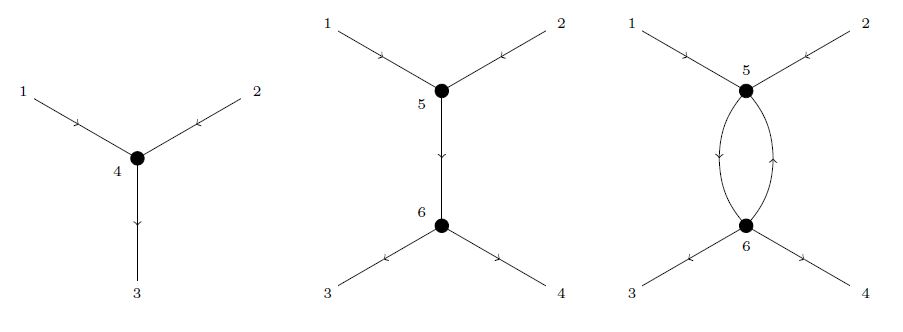
Beware that graphs need not be planar, may have edges between two external vertices (chords) and other effects not seen in these simple examples (… need to draw more generic examples…).
In particular, graphs may have tadpoles. But the next definition makes such graphs vanish in the graph complex:
Definition
(sign rules for graphs)
For a fixed finite linear order , consider the real linear span on the set of isomorphism classes (4) of graphs, according to Def. , with that set of external vertices:
The degree associated with a graph (Def. ) makes this a graded vector space.
On this real vector space, consider the linear equivalence relation generated by
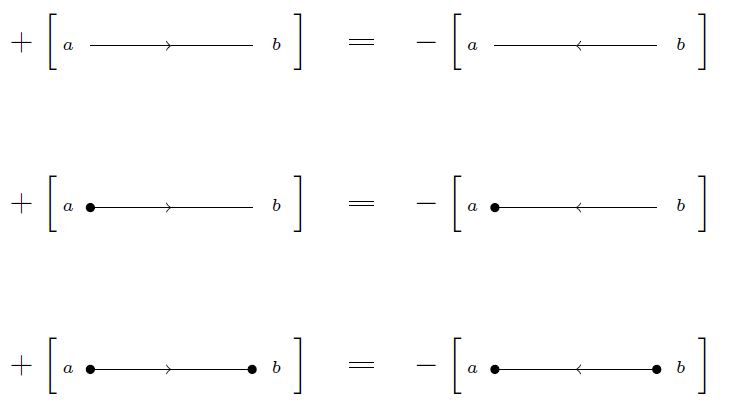
and
(Lambrechts-Volić 14, Def. 6.5 & Def. 6.5)
Since this equivalence relation is linear, the set of its equivalence classes is still a vector space, and since the equivalence relation also preserves the degrees (Def. ), it is still a graded vector space:
Definition
(graded vector space of graphs)
For , , we write
for the real graded vector space of equivalence classes under the sign rules (7) and (8) in the linear span (6) of the isomorphism classes of graphs (Def. ) with external vertices.
For any graph, we write
for the equivalence class of the element in this real graded vector space that it represents.
When there is not risk of confusion, we will still refer to this equivalence class as a graph.
A further quotient space of (9) will underly the actual graph complex below.
Example
(no tadpoles)
A direct consequence of quotienting out the equivalence relation (7) is that graphs with “tadpoles”, namely with edges that have coinciding source and target vertex, vanish in (9):
(This holds more generally for all with odd .)

Example
(trivalent graphs)
A graph without external vertices has degree (Def. ) equal to zero precisely if all its vertices (which are all internal, by assumption) are trivalent:
The following is the smallest example of such a trivalent graph:
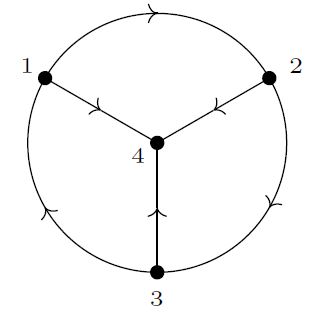
Hence in general, the degree of a trivalent graph is three times its number of external vertices:
(Because such a graph is the result of taking a trivalent graph in degree 0 and replacing internal vertices of degree -3 with external vertices of degree 0.)
For example, the following graph, obtained from the above trivalent graph by replacing the three internal vertices labeled 1,2 and 3 with external vertices, is of degree :
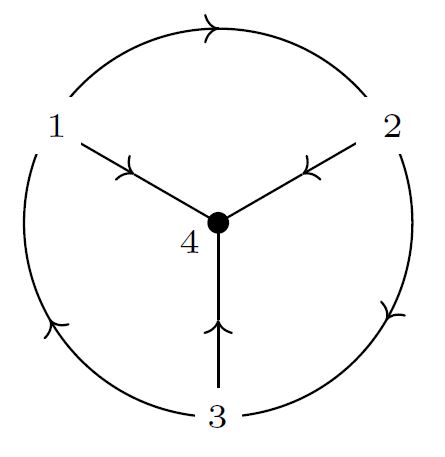
The algebra of graphs
Definition
(wedge product of graphs)
For
two equivalence classes (9) of isomorphism classes of graphs (Def. ) with the same number of external, their wedge product is the element
represented by the graph (Def. ) which is given by the disjoint union of linear orders of edges and internal vertices
It is immediate that:
Lemma
(graded commutative algebra of graphs)
For , the graded vector space (9) of graphs (Def. ) equipped with the wedge product of graphs from Def.
The differential on graphs
The differential on the graded vector space of equivalence classes of graphs (9) is defined in terms of contraction of certain edges in the graph (Def. below). For this we first say which edges count as contractible (Def. ) and which sign is picked up when contracting them (Def. ):
Definition
(contractible edges)
Given a graph (Def. ) we say that an edge is a contractible edge if the following conditions hold:
-
is not a tadpole (Example ):
-
has at least one internal vertex:
-
every internal vertex of is connected to more than just one other vertex, i.e. is not a solid arrow in a diagram of the following form

We write
for the subset of the contractible edges inside all edges of a graph .
Definition
(contraction of an edge)
Given a graph (Def. ) and a contractible edge (Def. ) consider the induced graph obtained by removing that edge and the one of its vertices with the larger label
and connecting all edges previously attached with the removed vertex to the remaining vertex of that edge (ie. the one with the smaller label):
(Lambrechts-Volić 14, Def. 6.9)
Remark
(sign of a contractible edge)
Given a contractible edge (Def. ) in some graph (Def. ) we associate a sign as follows:
where on the right we are identifying the linear order on the vertices with their natural number-labels as in (5).
Definition
(differential on graphs)
For a fixed finite linear order of external vertices, define on the graded vector space (9) a linear endomorphism given on the class (10) of a graph (Def. ) by the linear combination of all its edge contractions (Def. ) for all contractible edges (Def. ) weighted by their sign (Def. ):
Example
(differential of propagator graph vanishes)
The differential from Def. vanishes on all graphs without any internal vertices (since these have no contractible edges in the sense of Def. ). In particular it vanishes on the graph for the single Chern-Simons propagator:

Example
(differential on linear graphs)
The differential of Def. applied to the linear graph with one internal vertex:

Here the right hand side vanishes, due to the sign rule (7).
While this example illustrates the general action of the differential, beware that this particular differential relation will not actually contribute to the graph complex, as the graph on the left is a “vanishing graph” in the sense of Def. below (since the valence of the internal vertex is ).
Example
(differential of trivalent diagram with single internal vertex)
The image of the single trivalent internal vertex under the differential from Def. is as shown in the following:
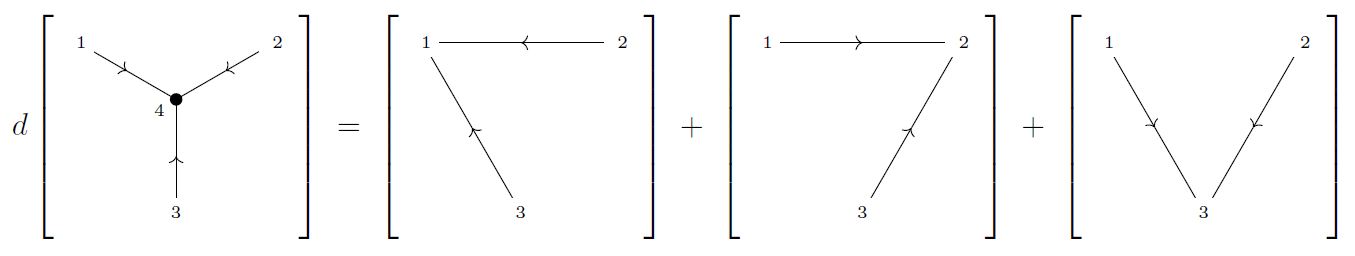
Under the quasi-isomorphism (1) from the graph complex to the de Rham complex on the Fulton-MacPherson compactification of a configuration space of points, given by sending each graph to its Chern-Simons Feynman amplitude on compactified configuration spaces of points (this Prop.), this relation becomes the “3-term relation” (this Prop.):
satisfied by the Chern-Simons propagator form
(Lambrechts-Volić 14, Figure 1 and 2)
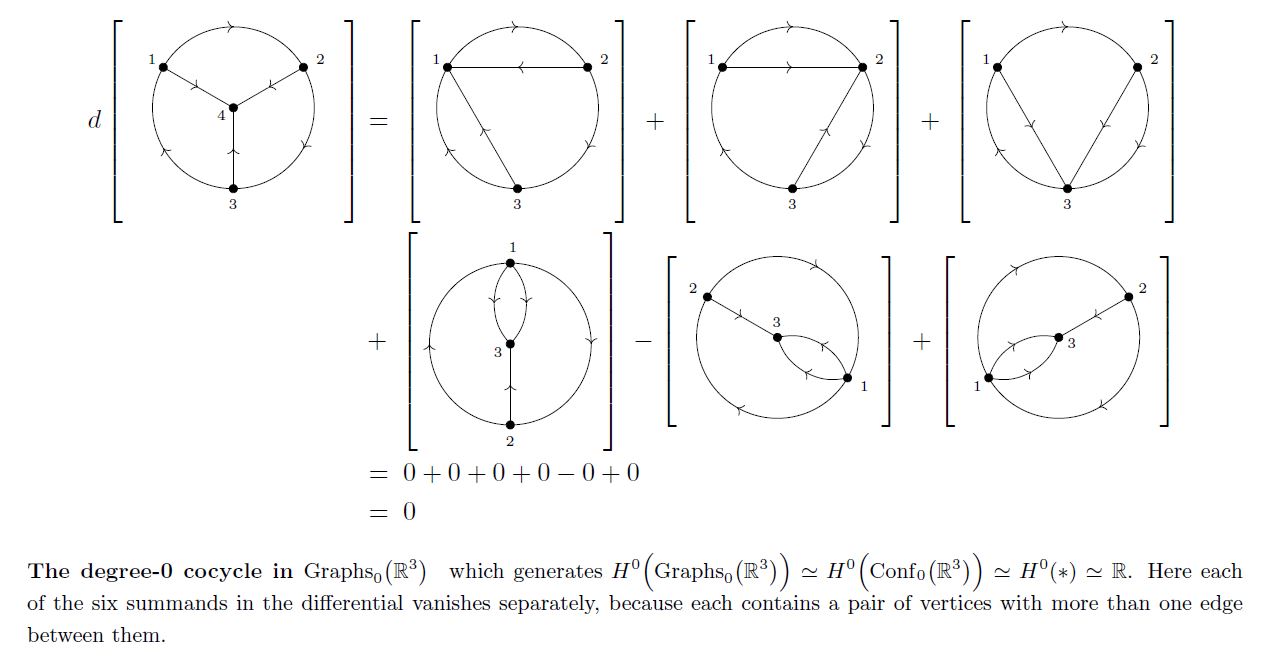
Example
(Differential of minimal trivalent vacuum diagram)
The differential of the minimum trivalent vacuum diagram from Example :
Example
(differential of trivalent tree with two internal vertices)
The differential (Def. ) on the trivalent tree with two internal vertices:

Lemma
(differential graded algebra structure)
The linear map in Def. makes the graded vector space a cochain complex, and, with its graded algebra-structure from Lemma in fact a differential graded algebra, in that:
-
(well defined) indeed only depends on the equivalence class ;
-
(degree) increases degree by +1
-
(nilpotency)
(Lambrechts-Volić 14, Lemmas 6.11 - 6.14)
The graph complex
Definition
(vanishing graphs)
We say that a graph (Def. ) is a vanishing graph if it is one or more of the following:
-
it is a tadpole-diagram: contains an edge with (Example );
-
it is a vacuum diagram: contains an internal vertex which is not connected, via some path of edges, to an external vertex;
-
it has parallel edges: contains a pair of vertices, with more than one edge between them, i.e. if the preimage contains more than one element.
-
it is less than trivalent: contains an internal vertex that is less than trivalent, hence an internal vertex with less than 3 edges attached to it;
Write
for the subspace spanned by vanishing graphs inside the graded vector space (9) of all graphs.
(Lambrechts-Volić 14, Def. 6.16)
Lemma
(vanishing graphs form a differential ideal)
The subspace of vanishing graphs (Def. ) is a differential ideal in the differential graded-commutative algebra of all graphs (Lemma ).
(Lambrechts-Volić 14, Lemma 6.17)
This implises that the quotient of all graphs by the vanishing graphs is still a differential graded-commutative algebra:
Definition
(graph complex)
For , the graph complex on external vertices is the differential graded-commutative algebra
of the differential graded-commutative algebra of all graphs (Lemma ) by its differential ideal (Lemma ) of vanishing graphs (Def. ).
(Lambrechts-Volić 14, Def. 6.19)
Example
(A 9-cocycle in )
The trivalent graph of degree 9 from Example is a cocycle in (Def. ):

The computation of the differential is just as for the 3-term relation in Example , but now all summands on the right have parallel edges and hence are vanishing graphs (Def. ) that are zero in the quotient (12) defining the graph complex (Def. ).
This trivalent diagram must be exact, as there is not supposed to be any cohomology in degree 9 (by Prop. ). What’s a trivializing coboundary?
Lemma
(graphs are in non-negative degree)
For all , the degrees (Def. ) of any non-vanishing graph in the graph complex (Def. ) are non-negative
Moreover, the only graphs of degree 0 are those containg the external vertices and nothing else:
Proof
Since tadpole graphs are vanishing graphs by Def. , we may assume that each edge in has two distint vertices it ends on, for otherwise we have the zero element in the graph complex.
Now, since each edge has degree 2 (according to Def. ), we may think of each edge as contribution a degree +1 for each of its two vertices, via the coresponding half-edge ending on that vertex.
Since external vertices have degree 0, together with the half-edges that end on them they contribute a non-negative number to the total degree.
While internal vertices have degree -3 (according to Def. ), we have a vanishing graph if less than three edges meet at an internal vertex (by Def. ) and hence, once vanishing graphs have been quotiented out, also internal vertices together with the half-edges ending on them contribute a non-negative number to the total degree.
This proves the first claim.
For the second claim, recall from Example that a graph has degree 0 precisely if it is a disjoint union of a) isolated external vertices and b) trivalent graphs all whose vertices are internal.
But if there is any disjoint non-empty sub-graph with only internal vertices, the total graph is again a vanishing graph by Def. , since it contains internal vertices not connected to any external vertex.
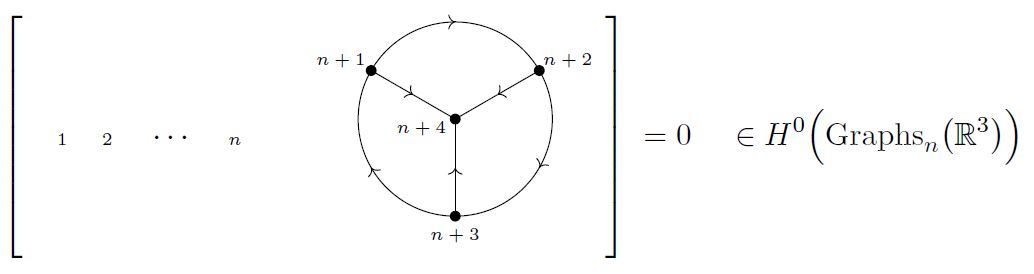
Hence the only non-vanishing graphs of degree 0 are those which have some isolated external vertices and nothing else.

(…)
2) Graph complexes modelling spaces of knots
We discuss graph complexes modelling the real cohomology of spaces of knots .
For the case of these were originally hinted at in Kontsevich 93, Section 5 and discussed in detail in Cattaneo, Cotta-Ramusino, Longoni 02 05, see also Bar-Natan 91. Review is in Volić 13, Section 4.
We state the definition of the graph complexes of knot graphs (according to the above) associated with Euclidean space of dimension 3, following Cattaneo, Cotta-Ramusino, Longoni 02 05.
The definition is almost exactly the same as that of above, except for the following two differences:
1) external vertices now carry degree -1, so that the formula (3) for the degree of a graph is changed to
(CCRL 02, (4.6), Volić 13, Def. 4.3)
2) There is implicit a contractible edge from the th to the st external vertex (an arc), in that the definition of the differential (Def. ) regards these as contractible edges.
(CCRL 02, 4.2, Volić 13, p. 35)
3) Apparently it must be understood that graphs whose labelling of external vertices differs by a cyclic permutation are identified. (?!)
(…)
Example
(knot graph cocycle of order 2)
The differential in of the single trivalent internal vertext is a variant of that in (Example ) and that in (Example ):

Notice how the edges parallel to the outer dashed arcs do not make the graphs in the first line vanish, but the parallel edges appearing in the second line make vanishing graphs (Def. ).
In contrast, the differential of the diagram in consisting of just two overlapping chords gets contributions only from contraction of the four arcs:
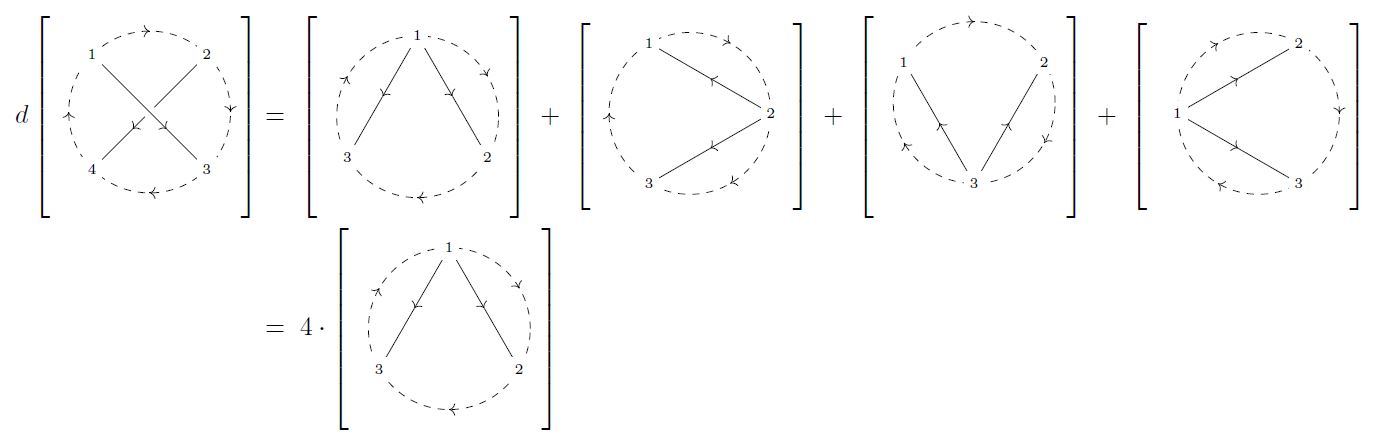
In both cases, the identification of graphs whose external labels are ccyclically permutated identifies the right hand sides of both these coboundaries with multiples of one and the same element in the graph complex.
Accordingly, the corresponding linear combination
is a cocycle of degree 0 in :

(Bar-Natan 91, 4.3.2, Cattaneo, Cotta-Ramusino, Longoni 02, Figure 2)
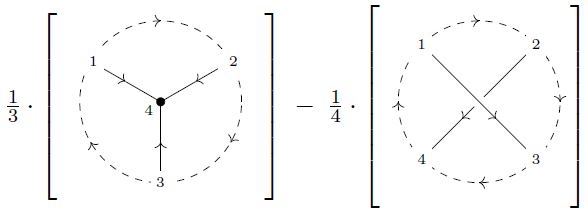
For the corresponding Feynman amplitude knot invariant see Prop. below.
Properties
under construction
Cohomology of configuration spaces via Feynman diagrams
Reading the graphs as Chern-Simons theory Feynman diagrams, hence as instructions for configuration space-integrals of wedge products of Feynman propagators assigned to edges in a graph, with propagators regarded as differential forms on configuration spaces, yields a quasi-isomorphism from the graph complex to the real cohomology of configuration spaces of points.
(Lambrechts-Volić 14, Section 9)
Proposition
(real cohomology of configuration spaces of ordered points in Euclidean space)
The real cohomology ring of the configuration spaces
of ordered points in Euclidean space is generated by elements
for
subject to these three relations:
-
;
-
;
-
.
Hence:
This is due to Arnold 69, Cohen 73.
| real cohomology of configuration space of points | graph complex (this Prop.) |
|---|---|
| generator | edge |
| relations: | relations: |
| graph changes sign when edge is reversed (Def. ) | |
| graph with parallel edges vanishes (Def. ) | |
| coboundary of trivalent vertex (Example ) |
Cohomology of knot space / higher Vassiliev invariants
The Feynman amplitudes of knot graphs (as above) are Vassiliev knot invariants.
This was originally hinted at in Kontsevich 93, Section 5. Details are in Cattaneo, Cotta-Ramusino, Longoni 02. Review is in Volić 13, Section 4.
Proposition
(knot invariant from Chern-Simons theory Feynman amplitude)
The Feynman amplitude of the knot graph cocycle Feynman diagram from Example , in Chern-Simons theory with a Wilson loop knot, is a knot invariant:
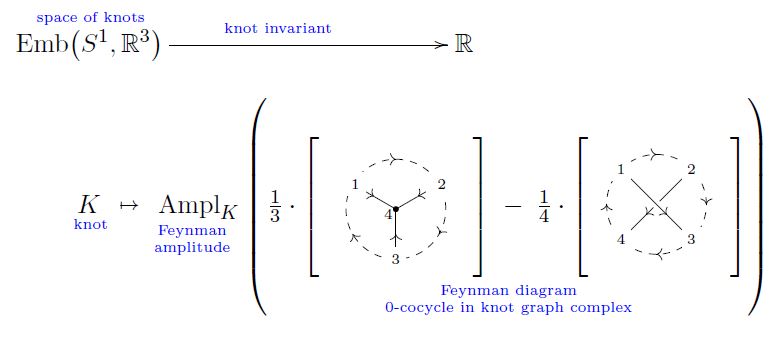
This is due to Guadagnini-Martellini-Mintchev 89 and Bar-Natan91, recalled im Volić 13, Theorem 3.3.5.
Various authors discuss Vassiliev invariants in terms of graphs subject to the “STU-relation”
(Kontsevich 93, Figure 8, Bar-Natan 95, Figure 3) and the “IHX-relation” which it implies (Bar-Natan 95, Theorem 6)
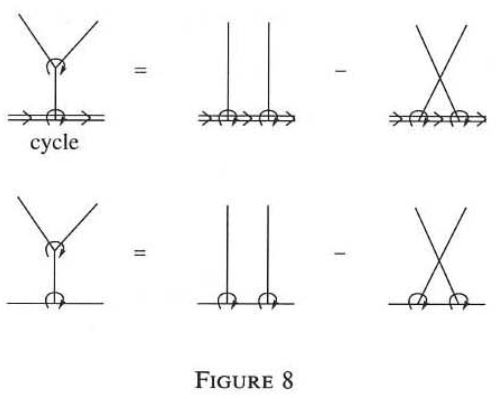
graphics grabbed from Kontsevich 93
That these relations characterize the cohomology of the knot-graph complex in the respective degrees is shown in Koytcheff-Munson-Volic 13, Section 3.4

graphics grabbed from Koytcheff-Munson-Volic 13
Cohomology of knot graph complex is weight systems on chord diagrams
cohomology of knot graph complex is weight systems on chord diagrams
Further applications
…moduli spaces
…deformation theory
…Rozansky-Witten theory
…description of the classifying space of the group of outer automorphisms of a free group with generators
… another graph complex controls the universal -deformations of the space of polyvector fields.
Related concepts
References
General
The rough definition of the graph complex, and its relation to Chern-Simons theory Feynman amplitudes and Vassiliev knot invariants was sketched in
-
Maxim Kontsevich, pages 11-12 of Feynman diagrams and low-dimensional topology, First European Congress of Mathematics, 1992, Paris, vol. II, Progress in Mathematics 120, Birkhäuser (1994), 97–121 (pdf)
-
Maxim Kontsevich, Section 5 of: Vassiliev’s knot invariants, Advances in Soviet Mathematics, Volume 16, Part 2, 1993 (pdf, pdf)
-
Maxim Kontsevich, around Def. 15 and Lemma 3 in Operads and Motives in Deformation Quantization, Lett. Math. Phys. 48 35-72, 1999 (arXiv:math/9904055)
Surveys
- Marko Berghoff, Graph complexes from the geometric viewpoint, arXiv.
In relation to configuration spaces of points:
- Ricardo Campos: Configuration Spaces of Points, CIM Bulletin 41 (2020) 41-47 [pdf, hal:03754254]
As a rational model for configuration spaces
A clean account and proof of the graph complex as a model for the rational homotopy type of the Fulton-MacPherson compactification of configuration spaces of points (exhibiting the formality of the little n-disk operads) is in
- Pascal Lambrechts, Ismar Volić, sections 6 and 7 and 9 of: Formality of the little N-disks operad, Memoirs of the American Mathematical Society no. 1079, 2014 (arxiv:0808.0457, doi:10.1090/memo/1079)
Discussion as a direct model for the rationalized homotopy groups of the configuration space of points:
- Pascal Lambrechts, Victor Tourtchine, Homotopy graph-complex for configuration and knot spaces, Transactions of the AMS, Volume 361, Number 1, January 2009, Pages 207–222 (arxiv:math/0611766)
further review:
- Benoit Fresse, Little discs operads, graph complexes and Grothendieck–Teichmüller groups, in Haynes Miller (ed.) Handbook of Homotopy Theory (arXiv:1811.12536)
Further discussion of the graph complex as a model for the de Rham cohomology of configuration spaces of points is in
-
Najib Idrissi, The Lambrechts-Stanley Model of Configuration Spaces, Invent. Math, 2018 (arXiv:1608.08054, doi:10.1007/s00222-018-0842-9)
-
Ricardo Campos, Thomas Willwacher, A model for configuration spaces of points (arXiv:1604.02043)
-
Ricardo Campos, Batalin-Vilkovisky formality and configuration spaces of points, 2017 (doi:10.3929/ethz-a-010886114)
-
Ricardo Campos, Najib Idrissi, Pascal Lambrechts, Thomas Willwacher, Configuration Spaces of Manifolds with Boundary (arXiv:1802.00716)
-
Ricardo Campos, Julien Ducoulombier, Najib Idrissi, Thomas Willwacher, A model for framed configuration spaces of points (arXiv:1807.08319)
See also
-
Maxim Kontsevich, Rozansky–Witten invariants via formal geometry, Compositio Mathematica 115: 115–127, 1999, doi, arXiv:dg-ga/9704009
-
Andrey Lazarev, Operads and topological conformal field theories, pdf; and older versio: Graduate lectures on operads and topological field theories, zip file with 11 pdfs, over 5 Mb
-
Alastair Hamilton, A super-analogue of Kontsevich’s theorem on graph homology, Lett. Math. Phys. 76 (2006), no. 1, 37–55, math.QA/0510390
-
A. Lazarev, Alexander Voronov, Graph homology: Koszul and Verdier duality (math.QA/0702313)
-
Mikhail Movshev, A definition of graph homology and graph K-theory of algebras (math.KT/9911111)
-
Kiyoshi Igusa, Graph cohomology and Kontsevich cycles, Topology 43 (2004), n. 6, p. 1469-1510, MR2005d:57028, doi
-
Vasily Dolgushev, Christopher Rogers, Thomas Willwacher, Kontsevich’s graph complex, GRT, and the deformation complex of the sheaf of polyvector fields (arxiv/1211.4230)
-
Damien Calaque, Carlo A. Rossi, Lectures on Duflo isomorphisms in Lie algebra and complex geometry, European Math. Soc. 2011
-
Sergei Merkulov, Graph complexes with loops and wheels, in (Manin’s Festschrift:) Algebra, Arithmetic, and Geometry, Progress in Mathematics 270 (2009) 311-354, doi, pdf
-
Martin Markl, Sergei Merkulov, Sergey Shadrin, Wheeled PROPs, graph complexes and the master equation, J. Pure Appl. Algebra 213(4):496–535, 2009, math.AT/0610683
The following survey has discussion of context between the graph complex and Batalin-Vilkovisky formalism:
-
Jian Qiu, Maxim Zabzine, Introduction to graded geometry, Batalin-Vilkovisky formalism and their applications, arxiv/1105.2680
-
Jian Qiu, Maxim Zabzine, Knot weight systems from graded symplectic geometry, arxiv/1110.5234
-
Alastair Hamilton, Andrey Lazarev, Graph cohomology classes in the Batalin-Vilkovisky formalism, J.Geom.Phys. 59:555-575, 2009, arxiv/0701825
As construction of higher order Vassiliev invariants
Discussion of the graph complex as computing higher order Vassiliev invariants, hence the real cohomology of spaces of knots (with the cohomology in degree-0 being the ordinary Vassiliev invariants):
-
Daniel Altschuler, Laurent Freidel, Vassiliev knot invariants and Chern-Simons perturbation theory to all orders, Commun. Math. Phys. 187 (1997) 261-287 (arxiv:q-alg/9603010)
-
Alberto Cattaneo, Paolo Cotta-Ramusino, Riccardo Longoni, Configuration spaces and Vassiliev classes in any dimension, Algebr. Geom. Topol. 2 (2002) 949-1000 (arXiv:math/9910139)
-
Alberto Cattaneo, Paolo Cotta-Ramusino, Riccardo Longoni, Algebraic structures on graph cohomology, Journal of Knot Theory and Its Ramifications, Vol. 14, No. 5 (2005) 627-640 (arXiv:math/0307218, doi:10.1142/S0218216505004019, math.GT/0307218, MR2006g:58021)
-
E. Guadagnini, E. Martellini, M. Mintchev, Chern-Simons field theory and link invariants, In: Knots, Topology and QuantumField Theories, Proceedings of the Johns Hopkins Workshop onCurrent Problems in Particle Theory 13, Florence (1989), World Scientific (doi:10.1142/9789814540742)
-
Dror Bar-Natan, Perturbative aspects of the Chern-Simons topological quantum field theory, thesis 1991 (spire:323500, proquest:303979053, BarNatanPerturbativeCS91.pdf)
Reviewed in:
- Ismar Volić, Section 4 of: Configuration space integrals and the topology of knot and link spaces, Morfismos, Vol 17, no 2, 2013 (arxiv:1310.7224)
Coproduct
Discussion of coproducts on a graph complex, given by decomposition of graphs into subgraphs and contractions of subgraphs:
-
Lucian Ionescu, Perturbative Quantum Field Theory and Configuration Space Integrals, In: John Byden, Advances in Topological Quantum Field Theory (arXiv:hep-th/0307062, doi:10.1007/978-1-4020-2772-7)
-
Lucian Ionescu, Cohomology of Feynman graphs and perturbative quantum field theory, In: O. Kovras, Focus on Quantum Field Theory, Nova Publishers Inc. 2004, (arXiv:math/0506142)
Cohomology
On the cochain cohomology of graph complexes:
Characterization of cohomology of (…) in terms of STU-relations and HKX-relations:
- Robin Koytcheff, Brian A. Munson, Ismar Volić, Section 3.4 of: Configuration space integrals and the cohomology of the space of homotopy string links, J. Knot Theory Ramif. 22, no. 11, 73 pp. (2013) (arXiv:1109.0056)
Concrete examples of cohomology classes in certain bi-degrees in by computer experiment:
- Dror Bar-Natan, Brendan McKay, Graph cohomology – An overview and some computations (pdf)
is the Lie algebra of the Grothendieck-Teichmüller group:
-
Thomas Willwacher, M. Kontsevich’s graph complex and the Grothendieck-Teichmueller Lie algebra, Invent. math. (2015) 200: 671 (arxiv:1009.1654)
-
Vasily Dolgushev, Christopher Rogers, Notes on Algebraic Operads, Graph Complexes, and Willwacher’s Construction, In: Mathematical aspects of quantization 583 (2012): 25-145. (arXiv:1202.2937)
-
Vasily Dolgushev, A manifestation of the Grothendieck-Teichmuellergroup in geometry (slides pdf)
See also:
- Kevin Morand, A note on multi-oriented graph complexes and deformation quantization of Lie bialgebroids (arXiv:2102.07593)
More:
- Anton Khoroshkin, Thomas Willwacher, Marko Živković, Differentials on graph complexes (arXiv:1411.2369)
More
In relation to Feynman rules:
- Marko Berghoff, Dirk Kreimer, Graph complexes and Feynman rules (arXiv:2008.09540)
Last revised on December 30, 2024 at 13:59:50. See the history of this page for a list of all contributions to it.