nLab Fulton-MacPherson operad
Context
Higher algebra
Algebraic theories
Algebras and modules
Higher algebras
-
symmetric monoidal (∞,1)-category of spectra
Model category presentations
Geometry on formal duals of algebras
Theorems
Topology
topology (point-set topology, point-free topology)
see also differential topology, algebraic topology, functional analysis and topological homotopy theory
Basic concepts
-
fiber space, space attachment
Extra stuff, structure, properties
-
Kolmogorov space, Hausdorff space, regular space, normal space
-
sequentially compact, countably compact, locally compact, sigma-compact, paracompact, countably paracompact, strongly compact
Examples
Basic statements
-
closed subspaces of compact Hausdorff spaces are equivalently compact subspaces
-
open subspaces of compact Hausdorff spaces are locally compact
-
compact spaces equivalently have converging subnet of every net
-
continuous metric space valued function on compact metric space is uniformly continuous
-
paracompact Hausdorff spaces equivalently admit subordinate partitions of unity
-
injective proper maps to locally compact spaces are equivalently the closed embeddings
-
locally compact and second-countable spaces are sigma-compact
Theorems
Analysis Theorems
Algebraic Quantum Field Theory
algebraic quantum field theory (perturbative, on curved spacetimes, homotopical)
Concepts
quantum mechanical system, quantum probability
interacting field quantization
Theorems
States and observables
Operator algebra
Local QFT
Perturbative QFT
Contents
Idea
A compactification of configuration spaces of points was introduced in Axelrod-Singer 93, p. 5-6, Fulton-MacPherson 94 and an operad-structure defined on it by Getzler-Jones 94 Kontsevich 97, now called the Fulton-MacPherson operad, weakly equivalent to the little n-disk operad (Salvatore 01, Prop. 4.9), hence a model for an En-operad.
The de Rham cohomology as well as the de Rham complex itself of the Fulton-MacPherson operad it quasi-isomorphic to graph complexes via topological Feynman amplitudes (see below), in fact it is the perturbative computation of Feynman amplitudes in Chern-Simons theory that motivated the compactified configuration space, this way, in Axelrod-Singer 91, Axelrod-Singer 93. These two quasi-isomorphism serve to exhibit formality of the Fulton-MacPherson operad, and hence also formality of the little n-disk operad.
To see the nature of the Axelrod-Singer-Fulton-MacPherson compactification of configuration spaces of points, observe that the configuration space of exactly 2 points in a Cartesian space/Euclidean space is homotopy equivalence to the quotient by Z/2 of a (d-1)-sphere
this being the sphere of directions of the vector pointing from one of the two points to the other. This means that the configuration space of points is homotopy equivalent to a quotient by the symmetric group of the Cartesian product of one such (d-1)-sphere of directions for each pair of points and various open intervals encoding the relative distance between the points.
The Fulton-MacPherson compactification is the evident compactification of this quotient of Cartesian products of (d-1)-spheres with open intervals, replacing the latter by their corresponding closed intervals.
This means that a point on the boundary of the Fulton-MacPherson compactification corresponds to a would-be configuration of points where some of the points have formally vanishing distance to each other, while still remembering a relative direction to each other.
More abstractly one may sum this up succinctly by saying that the ASFM-compactification is the blowup of the fat diagonal inside the Cartesian products of the base space with itself.
In the literature these boundary configurations are often referred to in terms of “infinitesimally close points”. While there may be some formal relation to actual infinitesimal neighbourhoods in (for example) synthetic differential geometry, we point out the Axelrod-Singer-Fulton-MacPherson compactifications as defined below are plain topological spaces or manifolds with corners (in some suitable sense), not objects in a smooth topos in any of the usual senses.
Definition
For , consider first the topological space of configurations of ordered n-tuples of points in the Cartesian space/Euclidean space , hence the mapping space of injections/embeddings of topological spaces
The group of translations and of scale transformations acts canonically on and hence diagonally on . The resulting quotient topological space
is clearly homotopy equivalent to the original space.
But now for this quotient space canonically carries the structure of a topological manifold (in fact of a smooth manifold) of dimension
while for the quotient is the point space (of dimension 0).
Now for a pair of distinct indices, consider the continuous function
which takes each configuration to the direction of the vector between the th and the th point in the configuration.
Moreover, for each triple of mutually distinct indices, consider the continuous function
which takes each configuration to the ratio of the distance between the th and the th point over that of the th to the th point.
Together these functions induce one total continuous function
from the ordered configuration space into the Cartesian product of all these (d-1)-spheres and intervals.
A moment of reflection shows that every ordered configuration modulo translation and rescaling, hence every point on the left, may be uniquely reconstructed from its direction vectors and distance ratios, hence from a point on the right, hence that this function is a homeomorphism onto its image (Sinha 03, lemma 3.18).
Definition
(Fulton-MacPherson compactification)
The Fultan-MacPherson compactification of the configuration space of ordered n-tuples of points in the Cartesian space/Euclidean space is the topological closure of the image of (2):
(e.g. Lambrechts-Volic 14, Def. 5.1)
The symmetric group still canonically acts on and hence the FM-compactification of the actual configuration space of points is the quotient space
Pictorial notation
By the above, the points on the boundary of a Fulton-MacPherson compactification of configuration spaces of points (Def. ) correspond to configurations that involve triples of points in space , such that the distance between two of them is “vanishing in ratio to the distance of both to the third”.
Hence where a configuration of two points in space looks like
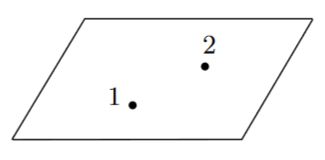
a configuration of such a boundary case of three points may be visualized as
where the “funnel” might be thought of as an infinite magnifying glass held to the location of the second point and revealing that it really consists of two points of vanishing distance to each other, relative to their joint distance to the remaining point.
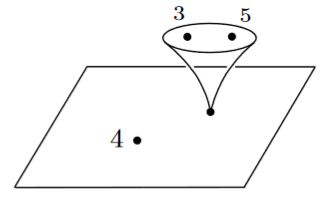
In this fashion, for instance a boundary point in the Fulton-MacPherson compactification depicted as follows

would consist of
-
points 3, 4 and 5 being arbitrarily close to each other with respect to their distance to points 1, 2 and 6
-
points 3 and 5 also being arbitrarily close to each other with respect to their joint distance to 4
-
points 1, 2 and 6 being arbitrarily close to each other in comparison to their joint distances to 3, 4 and 5
-
points 1 and 2 also being arbitrarily close to each other with respect to their joint distance to 6.
graphics grabbed from Lambrechts-Volic 14, Figures 3 and 4
This pictorial notation was introduced in Sinha 03. It immediately suggests the correct operad-structure on the Fulton-MacPherson compactifications.
Properties
Relation to the little -disk operad
Proposition
The Fulton-MacPherson operad is weakly equivalent in the model structure on operads with respect to the classical model structure on topological spaces, to the little d-disk operad.
(Salvatore 01, Prop. 4.9, summarized as Lambrechts-Volic 14, Prop. 5.6)
de Rham cohomology
We discuss the de Rham complex and the de Rham cohomology of Fulton-MacPherson compactifications.
Definition
Let (dimension of Euclidean space), and (number of points) and consider the Fulton-MacPherson compactification from Def. .
Let
be the standard volume form on the standard d-sphere.
For two distinct point labels, write
be the pullback of differential forms of this standard volume form along the projection from (1).
Proposition
Let (dimension of Euclidean space), and (number of points) and consider the Fulton-MacPherson compactification from Def. .
The de Rham cohomology of is, as a graded-commutative algebras, isomorphic to the quotient algebra of the free graded commutative algebra generated by the classes of the forms from Def.
by the following three relations (for all distinct ):
-
;
-
;
-
(“3-term relation”)
This is due to (Arnold 69, Cohen 73).
See also at configuration space of points the section Cohomology.
Remark
(real cohomology of the FM-compactification in terms of graph cohomology)
In the graph complex-model for the rational homotopy type of the ordered configuration space of points the three relations in Prop. are incarnated as follows:
-
a graph changes sign when one of its edges is reversed (this Def.)
-
a graph with parallel edges is a vanishing graph (this Def.)
-
the graph coboundary of a single trivalent internal vertex (this Example).
Relation to Graph complexes and Formality theorem
We have that the Fulton-MacPherson operad is formal in the sense that for each of its component manifolds (Def. ) there is a zig-zag of quasi-isomorphisms between their de Rham cohomology and their de Rham complex, and such that these morphisms are compatible with the induced cooperad-structure on both sides.
Concretely, the zig-zags may be taken to consist of one span of quasi-isomorphisms out of a suitable graph complex to the de Rham cohomology/de Rham complex of the Fulton-MacPherson operad.
Here the morphism from the graph complex to the de Rham complex of the Fulton-MacPherson operad regards the latter as the compactification of a configuration space of points, regards functions/differential forms on configuration spaces of points as n-point functions of a topological quantum field theory, regards suitable graphs as Feynman diagrams and proceeds by sending each such graph/Feynman diagram to a corresponding Feynman amplitude.
This idea of a proof was sketched in Kontsevich 99, a full account is due to Lambrechts-Volic 14.
Definition
(the graph complex)
For , write
for the graph complex of “Feynman graphs” with external vertices, regarded with its structure of a differential graded-commutative algebra over the real numbers.
(Lambrechts-Volic 14, Def. 6.19)
Proposition
The linear function
from the graph complex dgc-algebra (Def. ) to the de Rham cohomology (Prop. ) of the Fulton-MacPherson compactification (Def. ) given on generators by
(where are the differential forms from Def. )
extends to a homomorphism of dgc-algebras which is a quasi-isomorphism.
(Lambrechts-Volic 14, Theorem 8.1)
Example
(the “3-term relation”)
In the graph complex the differential of the graph as shown on the left below (the vertices on the horizontal line are the external vertices, that above the line is internal) is a linear combination as shown on the right:
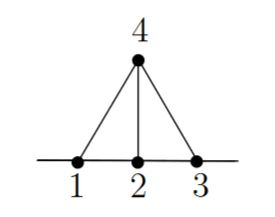

graphics grabbed from Lambrechts-Volic 14, Figure 1 & Figure 2
Under the above quasi-isomorphism (Prop. ) from the graph complex to the de Rham complex on the Fulton-MacPherson compactification of a configuration space of points given by sending each graph to its Chern-Simons Feynman amplitude on compactified configuration spaces of points (Remark ) this relation becomes the “3-term relation” from Prop.
satisfied by the Chern-Simons propagator form
Now we consider the analogous but richer quasi-isomorphism from the graph complex not just to the de Rham cohomology of the compactified configuration space, but its full de Rham complex.
Definition
(fiber integration over internal vertices)
For an element in the graph complex (Def. ) with internal vertices, write
for the evident continuous function between the Fulton-MacPherson compactifications of ordered configuration spaces of points (Def. ) obtained by forgetting the “internal” of the total of points in a configuration.
This canonically carries the structure of a fiber bundle of semi-algebraic manifolds and hence induces a fiber- integration of differential forms from minimal to partially algebraic differential forms:
(Lambrechts-Volic 14, Theorem 5.8 and equation (111))
Proposition
(quasi-isomorphism between graph complex and de Rham complex of Fulton-MacPherson compactification)
Consider the linear function
from the graph complex dgc-algebra (Def. ) to the semialgebraic de Rham complex (Def. ) of the Fulton-MacPherson compactification (Def. ) given on graphs
with
internal vertices by the integral transform of the canonical volume form through the span
where
-
the function on the left, to the Cartesian product of one (d-1)-spheres for each pair of distinct vertices, is given by the functions from (1)
-
the function on the right is the canonical forgetful projection from Def. ,
hence which sends
to the fiber integration over internal vertices (Def. ) of the wedge product of the differential forms
(Def. ), one for each edge in the graph from vertex to vertex .
This function constitutes a homomorphism of dgc-algebras which is a quasi-isomorphism.
That this is a dgc-algebra-homomorphism compatible with the cooperad-structure is proven in Lambrechts-Volic 14, that it is a quasi-isomorphism is proven in Lambrechts-Volic 14, section 10.
Remark
(perturbative Chern-Simons theory )
The differential forms from Def. may be understood as being the Feynman propagator of perturbative higher Chern-Simons theory regarded equivalently in its incarnation as a Feynman amplitude on compactified configuration spaces of points. See at Chern-Simons propagator for more on this.
From this perspective, the quasi-isomorphism in Prop. sends each graph, regarded as a Feynman diagram for higher Chern-Simons theory, to its correspomnding Feynman amplitude, regarded in its incarnation as a Feynman amplitude on compactified configuration spaces of points.
That this should be the case was originally suggested in Kontsevich 94.
Related concepts
References
The compactification of configuration spaces of points was first considered for two points in
-
Scott Axelrod, Isadore Singer, Chern-Simons Perturbation Theory, in S. Catto, A. Rocha (eds.) Proc. XXthe DGM Conf. World Scientific Singapore, 1992, 3-45; (arXiv:hep-th/9110056)
-
Scott Axelrod, Isadore Singer, Chern–Simons Perturbation Theory II, J. Diff. Geom. 39 (1994) 173-213 (arXiv:hep-th/9304087)
and then more generally in
- William Fulton, Robert MacPherson, A compactification of configuration spaces, Ann. of Math. (2), 139(1):183–225, 1994 (jstor:2946631)
based on the general method of resolution of singularities due to
- Heisuke Hironaka, Resolution of Singularities of an Algebraic Variety Over a Field of Characteristic Zero: I, Annals of Mathematics Second Series, Vol. 79, No. 1 (Jan., 1964), pp. 109-203 (95 pages) (jstor:1970486)
More general compactifications of spaces of subspace arrangements are due to
- Corrado de Concini, Claudio Procesi, Wonderful models of subspace arrangements, Selecta Mathematica, New Series Vol. 1, No. 3, 1995 (pdf)
see also
- Eva Maria Feichner, De Concini–Procesi Wonderful Arrangement Models: A Discrete Geometer’s Point of View, Math. Sci. Res. Inst. Publ 52, 2005 (pdf)
The operad-structure on Axelrod-Singer Fulton-MacPherson compactifications of configuration spaces of points was considered in
- Ezra Getzler, John Jones, Operads, homotopy algebra and iterated integrals for double loop spaces (arXiv:hep-th/9403055)
and alternatively in
-
Maxim Kontsevich, around Def. 12 of Operads and Motives in Deformation Quantization, Lett.Math.Phys.48:35-72,1999 (arXiv:math/9904055)
-
Maxim Kontsevich, section 5.1 of Deformation quantization of Poisson manifolds, I, Lett.Math.Phys.66:157-216,2003 (arXiv:q-alg/9709040)
which was corrected in
- Giovanni Gaiffi, Models for real subspace arrangements and stratified manifolds, Int. Math. Res. Not. 12:627-656, 2003 (pdf)
and developed in detail in
- Dev Sinha, Manifold theoretic compactifications of configuration spaces, Selecta Math. (N.S.) 10(3):391-428, 2004 (arXiv:math/0306385)
which also shows the equivalence to Fulton-MacPherson 94.
Review includes
- Pascal Lambrechts, Ismar Volić, section 5 of Formality of the little N-disks operad, Memoirs of the American Mathematical Society; no. 1079, 2014 (arXiv:0808.0457, doi:10.1090/memo/1079)
The de Rham cohomology was determined in
-
Vladimir Arnold, The cohomology ring of the colored braid group, Mat. Zametki, 1969, Volume 5, Issue 2, Pages 227–231 (mathnet:mz6827)
-
Fred Cohen, Cohomology of braid spaces, Bull. Amer. Math. Soc. Volume 79, Number 4 (1973), 763-766 (euclid:1183534761)
The equivalence to the little n-disk operad was established in
- Paolo Salvatore, Configuration spaces with summable labels, Cohomological methods in homotopy theory. Birkhäuser, Basel, 2001. 375-395.
The interpretation of the quasi-isomorphism establishing formality of the little n-disk operad as sending edges to Feynman propagators of some topological quantum field theory such as Chern-Simons theory is due to
- Scott Axelrod, Isadore Singer, Section 2 of Chern–Simons Perturbation Theory II, J. Diff. Geom. 39 (1994) 173-213 (arXiv:hep-th/9304087)
which is recalled and recast in somewhat more generality in
-
Raoul Bott, Alberto Cattaneo, Remark 3.6 in Integral invariants of 3-manifolds, J. Diff. Geom., 48 (1998) 91-133 (arXiv:dg-ga/9710001)
-
Alberto Cattaneo, Pavel Mnev, Remark 11 in Remarks on Chern-Simons invariants, Commun.Math.Phys.293:803-836,2010 (arXiv:0811.2045)
That this should exhibit a graph complex model for the cohomology of compactified configuration spaces was suggested in
- Maxim Kontsevich, pages 11-12 of Feynman diagrams and low-dimensional topology, First European Congress of Mathematics, 1992, Paris, vol. II, Progress in Mathematics 120, Birkhäuser (1994), 97–121 (pdf)
and spelled out in more detail in
with a careful proof being layed out in
Last revised on October 12, 2019 at 19:33:02. See the history of this page for a list of all contributions to it.