nLab quantum electrodynamics

Idea

Quantum electrodynamics (“QED”) is the perturbative quantum field theory of the electromagnetic field coupled to a Dirac field via the electron-photon interaction: it describes the quantum theory of photons and electrons.

Definition

The Lagrangian density defining QED is the sum of

1. the free field contribution of the electromagnetic field;

2. the free field contribution of a Dirac field;

3. the electron-photon interaction term with coupling constant given by the fine structure constant.

See at A first idea of quantum field theory this example.

The underlying free field theory admits a quantization via the corresponding Wick algebra. QED is, by definition, the perturbative quantum field theory obtained from this by finding a perturbative S-matrix for the electron-photon interaction.

As a result, scattering amplitudes for electron-photon interactions in QED are then expressed in terms of Feynman amplitudes:

Example

(Feynman amplitudes in causal perturbation theory – example of QED)

In perturbative quantum field theory, Feynman diagrams are labeled multigraphs that encode products of Feynman propagators, called Feynman amplitudes (this prop.) which in turn contribute to probability amplitudes for physical scattering processes – scattering amplitudes:

The Feynman amplitudes are the summands in the Feynman perturbation series-expansion of the scattering matrix

$$\mathcal{S} \left( S_{int} \right) = \underset{k \in \mathbb{N}}{\sum} \frac{1}{k!} \frac{1}{(i \hbar)^k} T( \underset{k \, \text{factors}}{\underbrace{S_{int}, \cdots , S_{int}}} )$$

of a given interaction Lagrangian density $L_{int}$.

The Feynman amplitudes are the summands in an expansion of the time-ordered products $T(\cdots)$ of the interaction with itself, which, away from coincident vertices, is given by the star product of the Feynman propagator $\Delta_F$ (this prop.), via the exponential contraction

$$T(S_{int}, S_{int}) \;=\; prod \circ \exp \left( \hbar \int \Delta_{F}^{a b}(x,y) \frac{\delta}{\delta \mathbf{\Phi}^a(x)} \otimes \frac{\delta}{\delta \mathbf{\Phi}(y)} \right) ( S_{int} \otimes S_{int} ) \,.$$

Each edge in a Feynman diagram corresponds to a factor of a Feynman propagator in $T( \underset{k \, \text{factors}}{\underbrace{S_{int} \cdots S_{int}}} )$, being a distribution of two variables; and each vertex corresponds to a factor of the interaction Lagrangian density at $x_i$.

For example quantum electrodynamics in Gaussian-averaged Lorenz gauge involves (via this example):

1. the Dirac field modelling the electron, with Feynman propagator called the electron propagator (this def.), here to be denoted

   $$\Delta \phantom{AAAA} \text{electron propagator}$$

2. the electromagnetic field modelling the photon, with Feynman propagator called the photon propagator (this prop.), here to be denoted

   $$G \phantom{AAAA} \text{photon propagator}$$

3. the electron-photon interaction

   $$L_{int} \;=\; \underset{ \text{interaction} }{ \underbrace{ i g (\gamma^\mu)^\alpha{}_\beta } } \, \underset{ { \text{incoming} \atop \text{electron} } \atop \text{field} }{\underbrace{\overline{\psi_\alpha}}} \; \underset{ { \, \atop \text{photon} } \atop \text{field} }{\underbrace{a_\mu}} \; \underset{ {\text{outgoing} \atop \text{electron} } \atop \text{field} }{\underbrace{\psi^\beta}}$$

The Feynman diagram for the electron-photon interaction alone is

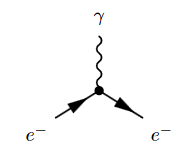
where the solid lines correspond to the electron, and the wiggly line to the photon. The corresponding product of distributions is (written in generalized function-notation)

$$\underset{ \text{loop order} }{ \underbrace{ \hbar^{3/2-1} } } \underset{ \text{electron-photon} \atop \text{interaction} }{ \underbrace{ i g (\gamma^\mu)^\alpha{}_\beta } } \,. \, \underset{ {\text{incoming} \atop \text{electron}} \atop \text{propagator} }{ \underbrace{ \overline{\Delta(-,x)}_{-, \alpha} } } \underset{ { \, \atop \text{photon} } \atop \text{propagator} }{ \underbrace{ G(x,-)_{\mu,-} } } \underset{ { \text{outgoing} \atop \text{electron} } \atop \text{propagator} }{ \underbrace{ \Delta(x,-)^{\beta, -} } }$$

Hence a typical Feynman diagram in the QED Feynman perturbation series induced by this electron-photon interaction looks as follows:

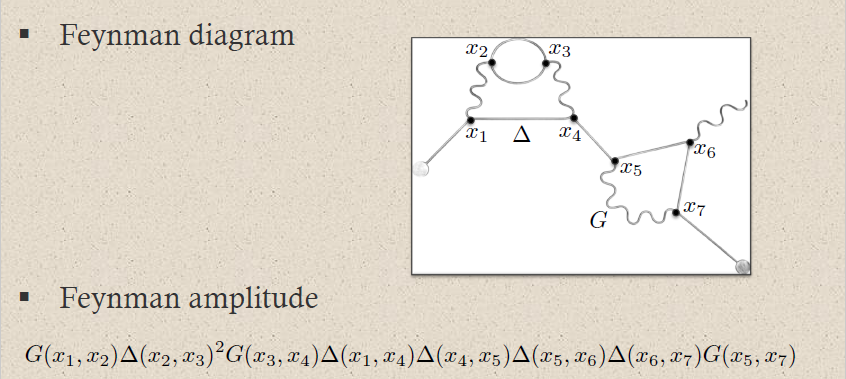
where on the bottom the corresponding Feynman amplitude product of distributions is shown; now notationally suppressing the contraction of the internal indices and all prefactors.

For instance the two solid edges between the vertices $x_2$ and $x_3$ correspond to the two factors of $\Delta(x_2,x_2)$:

This way each sub-graph encodes its corresponding subset of factors in the Feynman amplitude:

graphics grabbed from Brouder 10

A priori this product of distributions is defined away from coincident vertices: $x_i \neq x_j$. The definition at coincident vertices $x_i = x_j$ requires a choice of extension of distributions to the diagonal locus. This choice is the ("re-")normalization of the Feynman amplitude.

Properties

• anomalous magnetic moment of the electron

• Lamb shift

• Casimir effect

• axial anomaly

Related concepts

• fine structure constant

• photon propagator

• Schwinger effect

• quantum field theory

  • scalar field

  • gauge theory

    • QED

    • QCD, quantization of Yang-Mills theory

References

Original articles

The term “quantum electrodynamics” is due to

• Paul Dirac, The quantum theory of emission and absorption of radiation, Proc. Roy. Soc. London A 114, 243, 1927 (spire, pdf)

This left some issues with the quantization of the radiation field. These were addressed, and the causal propagator for the electromagnetic field was first found in

• Pascual Jordan, Wolfgang Pauli, Zur Quantenelektrodynamik ladungsfreier Felder, Zeitschrift für Physik 47, 151 (1928)

A comprehensive, albeit informal, theory of QED and of perturbative quantum field theory in general was eventually developed by

• Schwinger-Tomonaga-Feynman-Dyson, 1940s

For more on the history see

• Rudolf Haag, Early papers on quantum field theory (1992-1930) (pdf)

and (Scharf 95, section 0.0).

On quantum electrodynamics via discretized light-cone quantization:

• Andrew C. Tang, Discretized light cone quantization: Application to quantum electrodynamics, PhD thesis, Stanford (1990) [spire:296776, pdf, pdf]

• Andrew C. Tang, Stanley J. Brodsky, Hans-Christian Pauli, Discretized light-cone quantization: Formalism for quantum electrodynamics, Phys. Rev. D 44 (1991) 1842 [doi:10.1103/PhysRevD.44.1842]

Discussion of vacuum stability in QED:

• Günter Scharf, Vacuum stability in quantum field theory, Nuovo Cim. A109 (1996) 1605-1607 (spire:432208)

• Hrvoje Nikolić, Physical stability of the QED vacuum, 2001 (arXiv:hep-ph/0105176)

The rigorous construction of perturbative QED in causal perturbation theory is worked out in

• Scharf 95

and refined to perturbative AQFT in

• Michael Dütsch, Klaus Fredenhagen, A local (perturbative) construction of observables in gauge theores: the example of QED , Commun. Math. Phys. 203 (1999), no.1, 71-105, (arXiv:hep-th/9807078).

and generalized to possibly non-abelian Yang-Mills theory in

• Stefan Hollands, Renormalized Quantum Yang-Mills Fields in Curved Spacetime, Rev. Math. Phys. 20:1033-1172, 2008 (arXiv:0705.3340)

The weak adiabatic limit of QED was established in

• P. Blanchard and R. Seneor, Green’s functions for theories with massless particles (in perturbation theory), Ann. Inst. H. Poincaré Sec. A 23 (2), 147–209 (1975) (Numdam)

• Paweł Duch, Massless fields and adiabatic limit in quantum field theory (arXiv:1709.09907)

The local net of algebras of observables and hence the algebraic adiabatic limit was worked out in

• Dütsch-Fredenhagen 98

Further discussion of the adiabatic limit and infrared divergences includes

• Daniel Kapec, Malcolm Perry, Ana-Maria Raclariu, Andrew Strominger, Infrared Divergences in QED, Revisited, Phys. Rev. D 96, 085002 (2017) (arXiv:1705.04311)

Review

Traditional discussion includes

• Radovan Dermisek, Quantum Electrodynamics (QED) (pdf, pdf)

• Hitoshi Murayama, Quantum Electrodynamics (pdf)

• Eberhard Zeidler, Quantum field theory II: Quantum electrodynamics – A bridge between mathematicians and physicists, Springer (2009)

• Einan Gardi, lectures 19, 20 of Modern Quantum Field Theory, 2015 (pdf)

Mathematically rigorous discussion in causal perturbation theory/perturbative AQFT is in

• Günter Scharf, Finite Quantum Electrodynamics – The Causal Approach, Berlin: Springer-Verlag, 1995, 2nd edition

• Michael Dütsch, chapter 5 of From classical field theory to perturbative quantum field theory, 2018

  following (Dütsch-Fredenhagen 98)

Phenomenology

Comparison to experiment is reviewed in

• Tests of QED (pdf)

Specifically via the Lamb shift:

• Savely G. Karshenboim, D. I. Mendeleev, The Lamb Shift of Hydrogen and Low-Energy Tests of QED (arXiv:hep-ph/9411356)