nLab spherical braid group

Definition

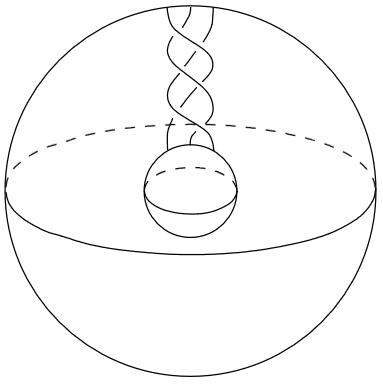
By the spherical braid group $Br_n(S^2)$, for $n \in \mathbb{N}$, one means the sphere braid group, hence the surface braid group, where the surface in question is the 2-sphere $S^2$. More concretely, the spherical braid group

$$Br_n(S^2) \;\simeq\; \pi_1 Conf_n(S^2) \,,$$

is the fundamental group $\pi_1(-)$ of the configuration space of $n$-points, $Conf_n(-)$, on the 2-sphere.

Illustrated on the right is the element $b_2 b_1 \in Br_3(S^2)$ (where $b_i$ denote the Artin braid generators, cf. Prop. .)

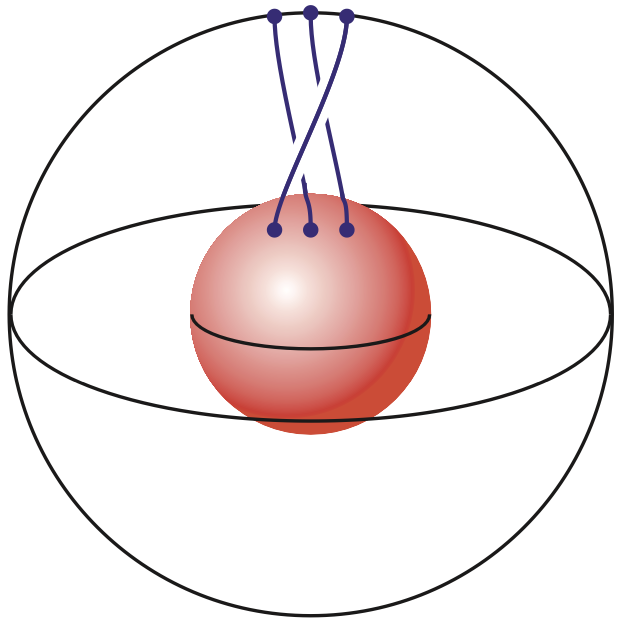
Beware that the spherical $n$-braid groups for $n \geq 3$ are not isomorphic to the mapping class groups of the $n$-punctured 2-sphere, see the examples there.

(Farb-Margalit '12 Fig. 9.6)

The generalized Birman sequence (here), which would superficially imply such isomorphism, does not apply to punctured spheres, since its assumption is violated: The map $C_2 \simeq \pi_1 Diff^{+}(S^2) \longrightarrow Br_n(S^2)$ is not trivial, whence the actual mapping class group is the quotient group of this normal subgroup-inclusion (cf. Farb & Margalit 2012 (9.1)), whose generator is the cyclic braid illustrated on the right.

Properties

(from math.SE:q/136821)

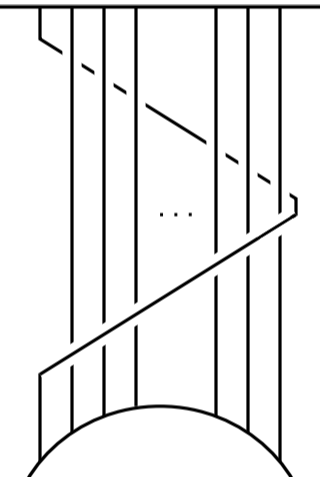
Proposition

The spherical braid group is the quotient group of the ordinary braid group by one further relation:

(1)$$Br_n(S^2) \;\simeq\; Br_n/ \big( (b_1 b_2 \cdots b_{n-1})(b_{n-1} \cdots b_2 b_1) \big) \,,$$

where the $b_i$ denote the Artin braid generators.

Moreover, the canonical map from the plain braid group to the symmetric group $Sym_n$ factors through the corresponding quotient coprojection:

(Fadell & Van Buskirk 1961 p 245, 255, cf. Tan 2024 §3.1)

Proposition

The order $\vert Br_n(S^2) \vert$ of the spherical braid group is:

1. $2$ for $n = 2$ (cf. Ex. ),

2. $12$ for $n =3$,

3. $\infty$ for $n \geq 4$.

(Fadell & VanBuskirk 1961 p 255)

Examples

Example

For $n = 2$ strands the ordinary braid group is free on the single Artin generator $b_1$,

$$Br_2 \;\simeq\; \langle b_1 \rangle \,\simeq\, \mathbb{Z} \,,$$

but the spherical braid group on $n = 2$ strands is cyclic of order 2, due to the relation (1):

$$Br_2(S^2) \;\simeq\; \langle b_1\rangle/\big(b_1^2\big) \,\simeq\, \mathbb{Z}/2 \,\eqqcolon\, C_2 \,.$$

Geometrically, the element $n \in \mathbb{Z}$ of the ordinary braid group $Br_2$ is the braid on two strands which makes $n$ half rotations in itself. But on the sphere, one full rotation (two half rotations) of one point around another may be contracted to a loop constant on the antipodal point.

(cf. Fadell & VanBuskirk 1961 p 254 and Prop. )

References

• Edward Fadell, James Van Buskirk: On the braid groups of $E^2$ and $S^2$, Bull. Amer. Math. Soc. 67 2 (1961) 211-213 [euclid:bams/1183524083]

• Benson Farb, Dan Margalit, around (9.1 in): A primer on mapping class groups, Princeton Mathematical Series, Princeton University Press (2012) [ISBN:9780691147949, jstor:j.ctt7rkjw, pdf]

• Cindy Tan: Smallest nonabelian quotients of surface braid groups, Algebr. Geom. Topol. 24 (2024) 3997-4006 [arXiv:2301.01872, doi:10.2140/agt.2024.24.3997]

On the representation theory of the spherical braid group:

• V. G. Bardakov: Linear Representations of the Braid Groups of Some Manifolds, Acta Appl Math 85 (2005) 41–48 [doi:10.1007/s10440-004-5584-6]