nLab structure identity principle
Context
Type theory
natural deduction metalanguage, practical foundations
type theory (dependent, intensional, observational type theory, homotopy type theory)
computational trinitarianism =
propositions as types +programs as proofs +relation type theory/category theory
Contents
Idea
By a stucture identity principle one means a statement of the form that all “identifications” of mathematical structures of a given type are necessarily structure respecting identifications (see also structuralism).
The source of the exact term “structure identity principle” seems to be Aczel (2011, slide 7), but the idea will have occurred earlier (see also the principle of equivalence).
The literature on the subject arguably suffers from absence of global conventions on how to name different notions of “identification” (identity, equality, isomorphism, equivalence, …), which can be confusing when speaking about a principle that is all about the fine-print of identifying two nominally different notions of identifications… But the general idea is always the same: Faced with notions of “direct”- and of “structure preserving”-identifications, a structure-identity-principle asserts that they are suitably identical.
Concretely, Aczel (2011, p. 9) declares that the structure identity principle (SIP) in homotopy type theory is the univalence axiom: This of course identifies terms of identification type between types with functions that are type-theoretic equivalences .
The latter is what Aczel (2011, p. 22) calls “isomorphisms”. While this matches the usage of the term “isomorphism” in abstract category theory to mean “invertible morphism”, to complete the notion of “structure identity” one may want a further argument to verify that such isomorphisms really are invertible *homo*-morphism with respect to some given mathematical structure (such as group structure etc.). Such enhancement of Aczel’s notion of SIP is considered in Coquand & Danielsson (2013) (who do not use the terminology “structure udentity principle”) and in UFP (2013, §9.8), Escardó (2019, §3.33.1) (who do).
Examples
To make this more concrete and more manifest, we may notice that:
-
at least a large class of kinds of mathematical structures on a base type are expressible as nothing but “telescopes” of dependent pairs of with an iteration of further dependent pair- and dependent function- and identification types (for examples, such as group structure, see here);
-
the univalence axiom implies extensionality principles for all three of these type formations (so with regards to UFP13 this is now using §2, instead), namely dependent function extensionality (here) and its analog for dependent pairs (here):
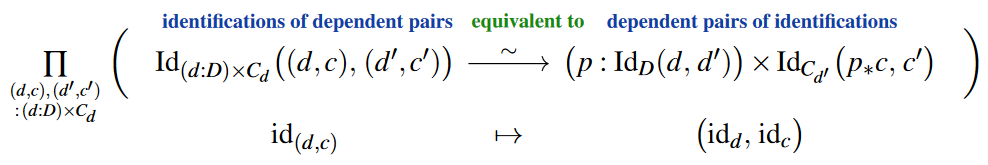

Together this means exactly that
-
identifications of two structured types which both are iterated dependent function-, dependent pair- and identity-types of the same form
-
are equivalent to giving the corresponding dependent function- and dependent pairing of componenwise identifications…
…and this is just what one wants to mean by “preserving” this structure as in the notion of homomorphisms.
For example, with the type of group structures defined as
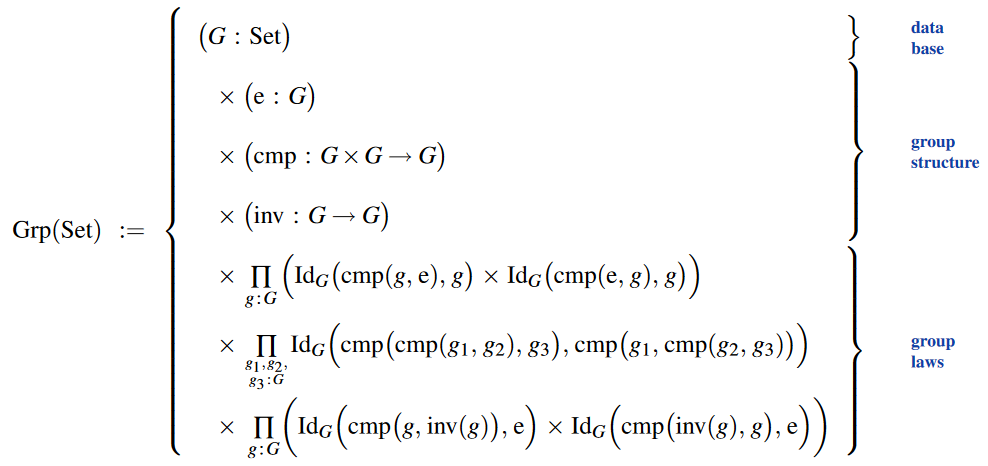
then the above extensionality principles (1) imply that the type of identifications of groups is equivalently that of bijections of the underlying types and equipped with the group homomorphism-property:
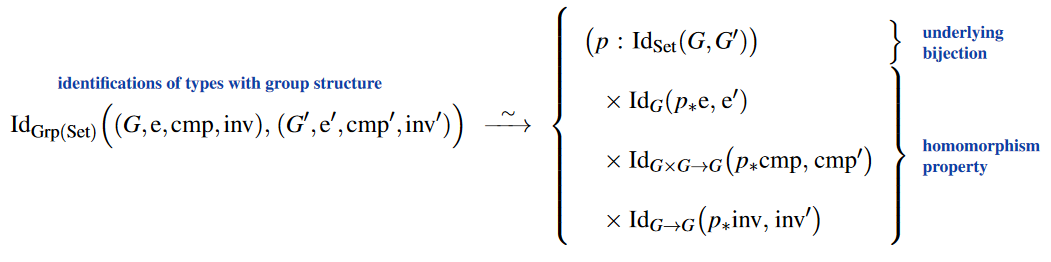
Related concepts
-
The idea of building the structure identity principle right into the inference rules for identifications in a type theory leads to the notion of (higher) observational type theory.
References
-
Peter Aczel, On Voevodsky’s Univalence Axiom, talk at Third European Set Theory Conference (2011) [pdf, pdf]
-
Thierry Coquand, Nils Anders Danielsson, Isomorphism is equality, Indagationes Mathematicae 24 4 (2013) 1105-1120 [doi:10.1016/j.indag.2013.09.002]
-
Univalent Foundations Project, §9.8 but also §2 of: Homotopy Type Theory – Univalent Foundations of Mathematics (2013) [web, pdf]
-
Martín Escardó, A structure identity principle for a standard notion of structure, §3.33.1 in: Introduction to Univalent Foundations of Mathematics with Agda [arXiv:1911.00580, webpage]
(formalized in the Agda proof assistant)
-
Benedikt Ahrens, Paige Randall North, Michael Shulman, Dimitris Tsementzis, A Higher Structure Identity Principle, LICS ‘20 (2020) 53–66 [arXiv:2004.06572, doi:10.1145/3373718.3394755]
-
Benedikt Ahrens, Paige Randall North, Univalent foundations and the equivalence principle, in: Reflections on the Foundations of Mathematics, Synthese Library 407 Springer (2019) [arXiv:2202.01892, doi:10.1007/978-3-030-15655-8]
-
Benedikt Ahrens, Paige Randall North, Michael Shulman, Dimitris Tsementzis, The Univalence Principle [abs:2102.06275]
Discussion in the context of the philosophy of structuralism:
- Dimitris Tsementzis, §5.1 in: Univalent foundations as structuralist foundations, Synthese 194 9 (2017) 3583–3617 [jstor:26748765, doi:10.1007/s11229-016-1109-x, pdf]
Last revised on June 14, 2025 at 18:25:42. See the history of this page for a list of all contributions to it.