nLab SO(8)
Context
Group Theory
- group, ∞-group
- group object, group object in an (∞,1)-category
- abelian group, spectrum
- super abelian group
- group action, ∞-action
- representation, ∞-representation
- progroup
- homogeneous space
Classical groups
Finite groups
Group schemes
Topological groups
Lie groups
Super-Lie groups
Higher groups
Cohomology and Extensions
Related concepts
Contents
Idea
Among all special orthogonal groups , the case of is special, since in the ADE classification of simple Lie groups it corresponds to D4, which makes its representation theory enjoy triality.
Properties
Subgroup lattice
Proposition
(Spin(7)-subgroups in Spin(8))
There are precisely 3 conjugacy classes of Spin(7)-subgroups inside Spin(8), and the triality group acts transitively on these three classes.
(Varadarajan 01, Theorem 5 on p. 6, see also Kollross 02, Prop. 3.3 (1))
Proposition
(G₂ is intersection of Spin(7)-subgroups of Spin(8))
The intersection inside Spin(8) of any two Spin(7)-subgroups from distinct conjugacy classes of subgroups (according to Prop. ) is the exceptional Lie group G₂, hence we have pullback squares of the form
(Varadarajan 01, Theorem 5 on p. 13)
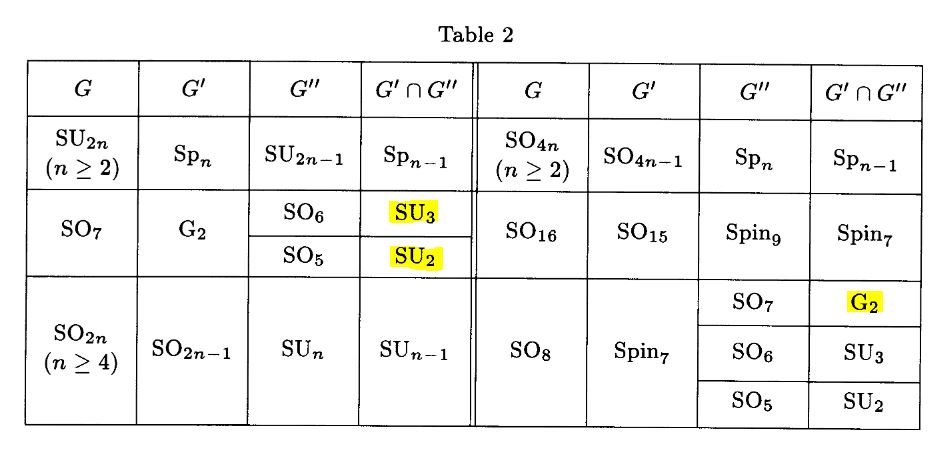
Proposition
We have the following commuting diagram of subgroup inclusions, where each square exhibits a pullback/fiber product, hence an intersection of subgroups:
Here in the bottom row we have the Lie groups
Spin(5) Spin(6) Spin(7) Spin(8)
with their canonical subgroup-inclusions, while in the top row we have
and the right vertical inclusion is one of the two non-standard inclusions, according to Prop. .
Proof
The square on the right is that from Prop. .
The square in the middle is Varadarajan 01, Lemma 9 on p. 10.
The statement also follows with Onishchik 93, Table 2, p. 144:
Proposition
(Spin(5).Spin(3)-subgroups in SO(8))
The direct product group SO(3) SO(5) together with the groups Sp(2).Sp(1) and , with their canonical inclusions into SO(8), form 3 conjugacy classes of subgroups inside SO(8), and the triality group acts transitively on these three classes.
Similarly:
Proposition
(Spin(5).Spin(3)-subgroups in Spin(8))
The groups Spin(5).Spin(3), Sp(2).Sp(1) and , with their canonical inclusions into Spin(8), form 3 conjugacy classes of subgroups inside Spin(8), and the triality group acts transitively on these three classes.
In summary we have these subgroup inclusions
permuted by triality:
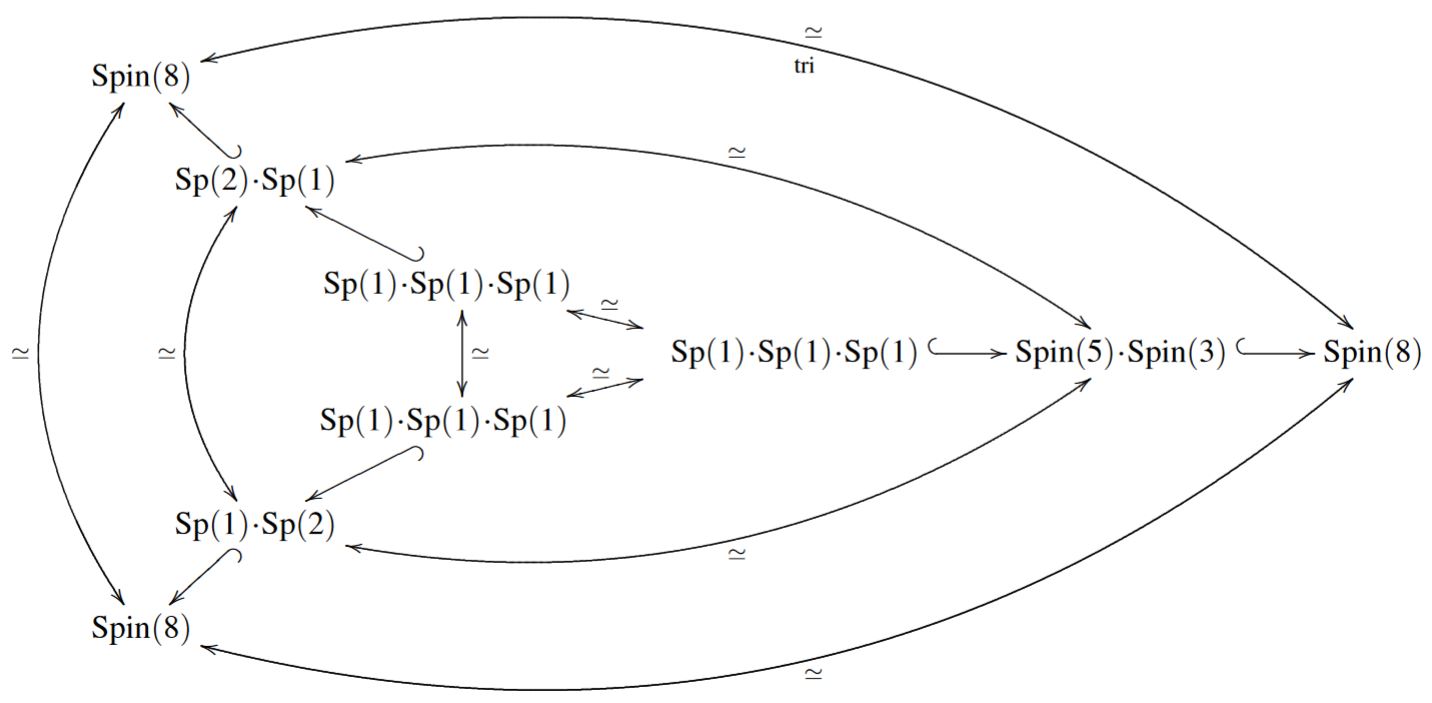
graphics grabbed from FSS 19, Sec. 3.3
Homotopy groups
The homotopy groups of in low degrees:
| 0 |
Cohomology of classifying spaces
Proposition
The ordinary cohomology ring of the classifying space is:
1) with coefficients in the cyclic group of order 2:
where are the universal Stiefel-Whitney classes,
and where
2) with coefficients in the integers:
where is the first fractional Pontryagin class, is the second Pontryagin class, is the Euler class, and
is the Bockstein homomorphism.
Moreover, we have the following relations:
This is due to Quillen 71, Čadek-Vanžura 95, see Čadek-Vanžura 97, Lemma 4.1.
Proposition
Consider the delooping of the triality automorphism relating Sp(2).Sp(1) with Spin(5).Spin(3) (Prop. ) on classifying spaces
Then the pullback of the universal characteristic classes of (from Prop. ) along is as follows:
In fact .
Hence, in rational cohomology:
-Structure and exceptional geometry
Spin(8)-subgroups and reductions to exceptional geometry
see also: coset space structure on n-spheres
Related concepts
rotation groups in low dimensions:
see also
References
General
- Robert Bryant, Remarks on Spinors in Low Dimension (pdf, pdf)
See also
- Wikipedia, SO(8)
Subgroup lattice
On the subgroup lattice of Spin(8)
-
A. L. Onishchik (ed.) Lie Groups and Lie Algebras
-
I. A. L. Onishchik, E. B. Vinberg, Foundations of Lie Theory,
-
II. V. V. Gorbatsevich, A. L. Onishchik, Lie Transformation Groups
Encyclopaedia of Mathematical Sciences, Volume 20, Springer 1993
-
-
Veeravalli Varadarajan, Spin(7)-subgroups of SO(8) and Spin(8), Expositiones Mathematicae Volume 19, Issue 2, 2001, Pages 163-177 (doi:10.1016/S0723-0869(01)80027-X, pdf)
-
Martin Čadek, Jiří Vanžura, On and -structures in 8-dimensional vector bundles, Publicacions Matemàtiques Vol. 41, No. 2 (1997), pp. 383-401 (jstor:43737249)
-
Megan M. Kerr, New examples of homogeneous Einstein metrics, Michigan Math. J. Volume 45, Issue 1 (1998), 115-134 (euclid:1030132086)
-
Andreas Kollross, Prop. 3.3 of A Classification of Hyperpolar and Cohomogeneity One Actions, Transactions of the American Mathematical Society Vol. 354, No. 2 (Feb., 2002), pp. 571-612 (jstor:2693761)
Discussion with an eye towards foundations of M-theory:
- Domenico Fiorenza, Hisham Sati, Urs Schreiber, Twisted Cohomotopy implies M-theory anomaly cancellation (arXiv:1904.10207)
Cohomology
The integral cohomology of the classifying spaces and and the action of triality on these is discussed in
-
Alfred Gray, Paul S. Green, Sphere transitive structures and the triality automorphism, Pacific J. Math. Volume 34, Number 1 (1970), 83-96 (euclid:1102976640)
-
Daniel Quillen, The mod 2 cohomology rings of extra-special 2-groups and the spinor groups, Math. Ann . 194 (1971), 19
-
Martin Čadek, Jiří Vanžura, On the existence of 2-fields in 8-dimensional vector bundles over 8-complexes, Commentationes Mathematicae Universitatis Carolinae, vol. 36 (1995), issue 2, pp. 377-394 (dml-cz:118764)
-
Martin Čadek, Jiří Vanžura, Section 2 of On and -structures in 8-dimensional vector bundles, Publicacions Matemàtiques Vol. 41, No. 2 (1997), pp. 383-401 (jstor:43737249)
Last revised on July 18, 2024 at 11:19:53. See the history of this page for a list of all contributions to it.