nLab suspension type
Context
Type theory
natural deduction metalanguage, practical foundations
type theory (dependent, intensional, observational type theory, homotopy type theory)
computational trinitarianism =
propositions as types +programs as proofs +relation type theory/category theory
Homotopy theory
homotopy theory, (∞,1)-category theory, homotopy type theory
flavors: stable, equivariant, rational, p-adic, proper, geometric, cohesive, directed…
models: topological, simplicial, localic, …
see also algebraic topology
Introductions
Definitions
Paths and cylinders
Homotopy groups
Basic facts
Theorems
Contents
Idea
In homotopy type theory, a suspension type of any type is the pushout type of the terminal function (to the unit type) along itself, hence the pushout of the span .
The categorical semantics is given by suspension objects in homotopy theory (and hence by suspension of topological spaces in, say, the classical model structure on topological spaces).
Definition
As a higher inductive type, the (unreduced) suspension of a type is generated by
-
A term
-
a term
-
A function
(to the identity type of ).
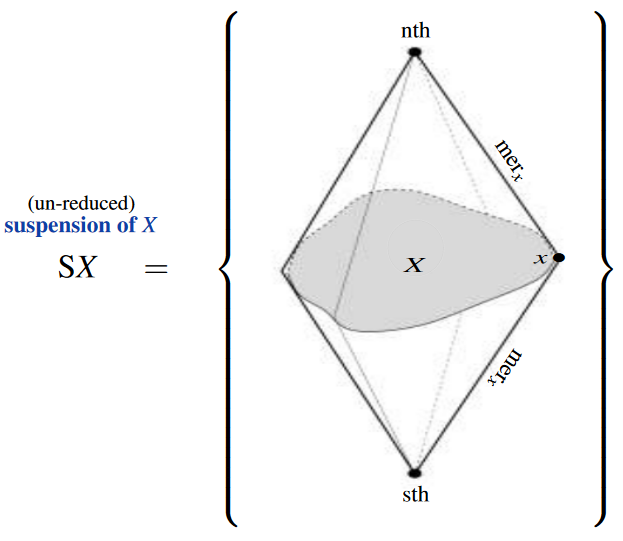
(graphics adapted from Muro 2010)
The resulting inference rules are the specialization of those of pushout types (see there).
In Coq pseudocode this becomes
Inductive Suspension (X \colon Type) : Type
| nth : Suspension X
| sth : Suspension X
| mer : X -> Id Suspension X nth sthThis says that the type is dependent on the type and inductive constructed from two terms in the suspension, whose interpretation is as the north and south poles of the suspension, together with a term in the function type from to the identity type of paths between these two terms, representing the meridians from the north to the south pole.
Examples
-
The two-valued type is the suspension type of the empty type .
-
The interval type is the suspension type of the unit type .
-
The circle type is the suspension type of .
-
The homotopical disk type is the suspension type of .
-
Homotopical -sphere types of dimension , , are suspension types of .
-
Homotopical -globe types of dimension , , are suspension types of .
Related concepts
-
-
suspension type, reduced suspension type
-
References
Last revised on February 22, 2024 at 06:34:23. See the history of this page for a list of all contributions to it.