Schreiber Proper Orbifold Cohomotopy for M-Theory
A talk that I have given:
-
Urs Schreiber on joint work with Hisham Sati:
Proper Orbifold Cohomotopy for M-Theory
talk at:
New Geometry of 21st Century – II
via NUS Singapore, Nov-Dec 2021
download
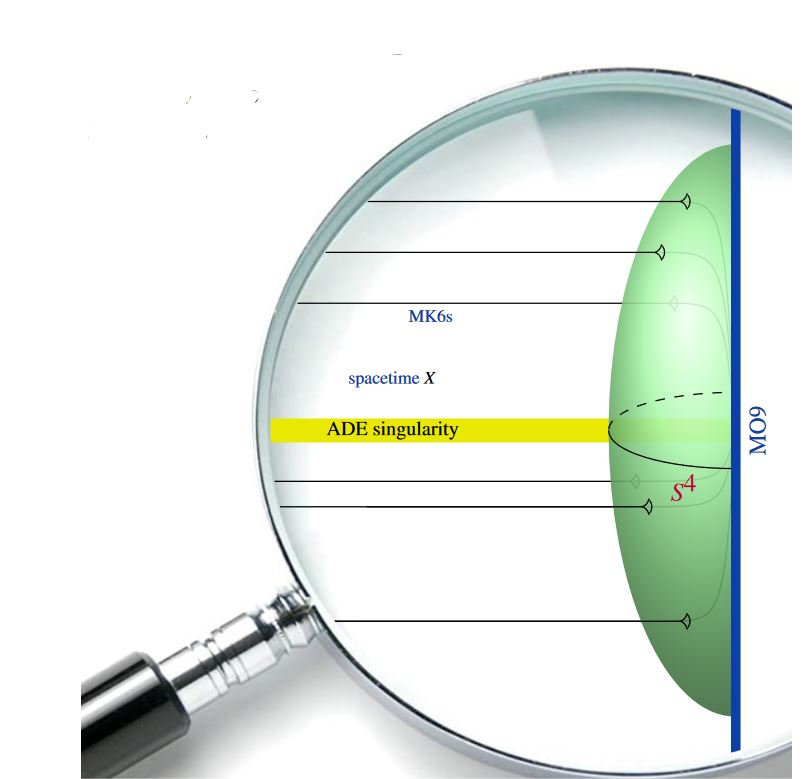
Abstract. M-theory folklore has it that all quasi-realistic QCD-like quantum physics is realized (and thereby non-perturbatively completed) at or inside super-spacetime orbi-singularities of intersecting black M5/M2-branes, whose higher magnetic flux threads an ambient smooth G-structured bulk super-spacetime subject to a long list of subtle differential- and algebro-topological constraints (such as shifted C-field flux quantization, C-field tadpole/RR-field tadpole cancellation, GS-anomaly cancellation, etc.).
Despite an intriguing web of plausibility arguments and consistency checks that have been amassed since this picture emerged in the “second superstring revolution”, it has remained unclear, and largely unexplored, what any of this really means mathematically – notably what putative M-theory on fluxed and G-structured super-orbifold spacetimes actually predicts, with any certainty, for observable physics – be it in its application to confined hadronic matter (holographic QCD), or to quantum-supreme solid states (holographic CMT), not to speak of the more traditional but less tangible application to quantum gravity.
The issue with the mathematical foundations of M-theory (formerly known as string theory) had been prophesized early on (E. Witten 1988, in Davis & Brown, CUP 1988, p. 95, 102): “String theory at its finest should be a new branch of geometry developed in the twenty-first or twenty-second century that fell by chance into the twentieth century”.
With the 21st century now well under way, this talk surveys a new branch of mathematical geometry which has emerged over the last years, in joint work with Hisham Sati, and which provably exhibits a fair number of the subtle phenomena expected in M-theory on fluxed orbifold spacetimes:
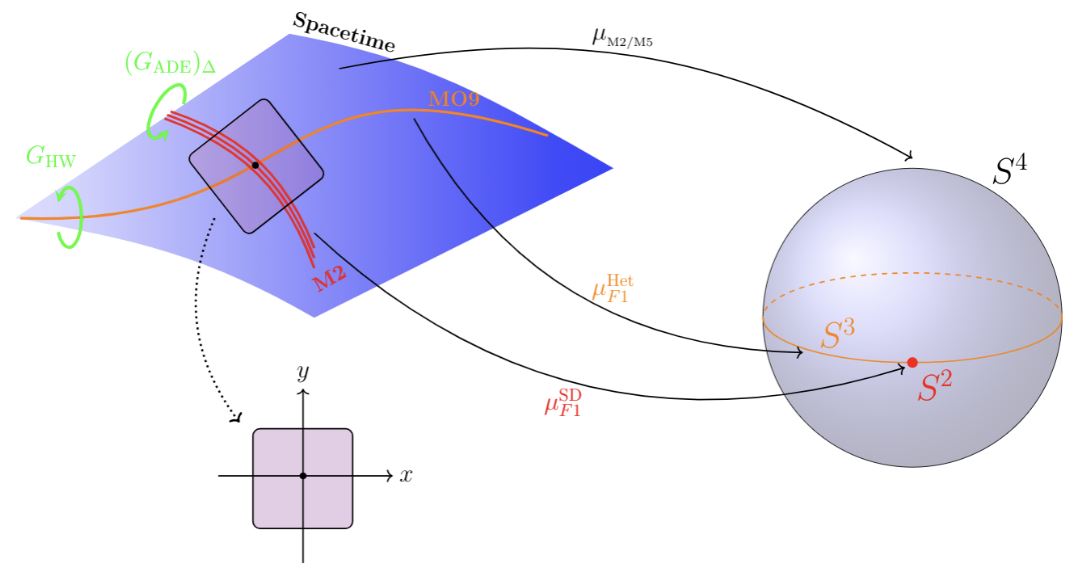
This “differential cohomotopy in a singular-cohesive homotopy-topos” (arXiv:2008.01101) operates close to novel homotopy-theoretic foundations for mathematics itself (modal/cohesive homotopy type theory) and provides a rigorous but charmingly intuitive axiomatics of geometric qualities that transparently control elaborate higher geometric entities such as the twisted equivariant differential generalized cohomology of G-structured super-orbifolds which should give mathematical meaning to quantized M-brane charges and C-field fluxes.
In this talk I will try to give some idea of the basics and of some applications and results, following the references listed below.
Evidence for the natural “Hypothesis H” that this new geometry is part of the missing mathematical foundations of M-theory is further discussed in the lecture by Hisham Sati in the school the week before this conference.
Related talks:
-
Some Quantum States of M-Branes under Hypothesis H
Centre for Research in String Theory
QMU London, December 2021
-
Microscopic Brane Physics from Cohomotopy
talk at M-Theory and Mathematics
NYU Abu Dhabi, 2020
-
Equivariant Cohomotopy and Branes
String and M-Theory:
The New Geometry of the 21st Century,NUS Singapore, December 2018
-
Equivariant Super Homotopy Theory
Geometry in Modal Homotopy Type Theory
CMU Pittsburgh, March 2019
Related articles:
-
John Huerta, Hisham Sati, Urs Schreiber:
Real ADE-equivariant (co)homotopy and Super M-branes
Comm. Math. Phys. 371 (2019) 425–524
-
Equivariant Cohomotopy implies orientifold tadpole cancellation
J. Geom. Phy. 156 (2020) 103775
-
Simon Burton, Hisham Sati, Urs Schreiber:
Lift of fractional D-brane charge to equivariant Cohomotopy theory
J. Geom. Phys. 161 (2021) 104034
For more
see the pointers at Hypothesis H.
Last revised on December 8, 2021 at 16:35:16. See the history of this page for a list of all contributions to it.