nLab geometric engineering of quantum field theory
Context
Quantum field theory
Physics
physics, mathematical physics, philosophy of physics
Surveys, textbooks and lecture notes
theory (physics), model (physics)
experiment, measurement, computable physics
-
-
-
Axiomatizations
-
Tools
-
Structural phenomena
-
Types of quantum field thories
-
String theory
Ingredients
Critical string models
Extended objects
Topological strings
Backgrounds
Phenomenology
Contents
Idea
The embedding of aspects of quantum field theories into sectors of string theory – where gauge enhancement happens near orbifold singularities/O-planes and/or on the worldvolumes of branes (e.g. super Yang-Mills theory on D-branes, 6d (2,0)-superconformal QFT on M5-branes) encodes QFT properties in terms of the background geometry in a useful way, for instance the various dualities of string theory will relate different QFTs in way that are typically far from obvious from just looking at these QFTs themselves.
The investigation specifically of N=2 D=4 super Yang-Mills theory and N=1 D=4 super Yang-Mills theory in this fashion has come to be known as geometric engineering of quantum field theory (Katz, Klemm & Vafa 1997, Katz-Klemm 96 ).
Specifically, the geometrically engineered QFTs are those on the worldvolume of black D-branes that end on (are suspended between) black NS5-branes (due to Hanany-Witten 97, review includes Fazzi 17). See at D-branes ending on NS5-branes.
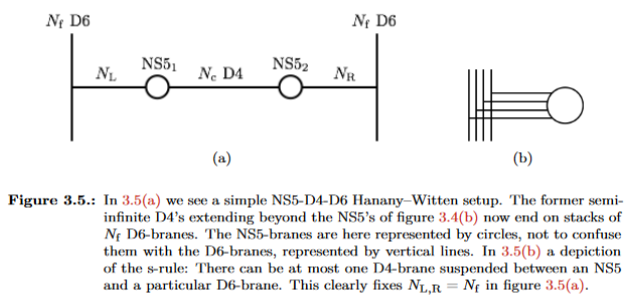
graphics grabbed from Fazzi 17, p. 25

graphics grabbed from Fazzi 17, p. 32
For more relations between QFTs found via string theory see at string theory results applied elsewhere.
Related concepts
References
The following lists mainly references that explicitly mention the term “geometric engineering” or variants. But the idea of geometric engineering of QFT in string/M-theory is much more wide-spread and not always referred to by this terminology (cf. for instance at M-theory on G2-manifolds, gauge enhancement and at intersecting D-brane models).
General
The original articles:
-
Sheldon Katz, Cumrun Vafa: Matter From Geometry, Nucl. Phys. B 497 (1997) 146-154 [arXiv:hep-th/9606086, doi:10.1016/S0550-3213(97)00280-0]
-
Sheldon Katz, Albrecht Klemm, Cumrun Vafa: Geometric Engineering of Quantum Field Theories, Nucl. Phys. B 497 (1997) 173-195 [doi:10.1016/S0550-3213(97)00282-4, arXiv:hep-th/9609239]
-
Sheldon Katz, Cumrun Vafa, Geometric Engineering of Quantum Field Theories, Nucl.Phys. B 497 (1997) 196-204 [doi:10.1016/S0550-3213(97)00283-6, arXiv:hep-th/9611090]
-
Amihay Hanany, Edward Witten: Type IIB Superstrings, BPS Monopoles, And Three-Dimensional Gauge Dynamics, Nucl. Phys. B 492 (1997) 152-190 [doi:10.1016/S0550-3213(97)80030-2, arXiv:hep-th/9611230]
-
Mina Aganagic, Cumrun Vafa: Manifolds, Mirror Symmetry and Geometric Engineering [arXiv:hep-th/0110171]
Review:
-
Amit Giveon, David Kutasov: Brane Dynamics and Gauge Theory, Rev. Mod. Phys. 71 (1999) 983-1084 [arXiv:hep-th/9802067 doi:10.1103/RevModPhys.71.983]
-
Andreas Karch: Field Theory Dynamics from Branes in String Theory, PhD thesis, Berlin (1998) [doi:10.18452/14371]
-
David Morrison, Limitations of Geometric Engineering: Implications for Model Building, talk (2008) [slides:pdf]
-
Moritz Kuentzler: Elliptic Fibrations for F-Theory Geometric Engineering (2014) PhD thesis [webpage, pdf]
-
Marco Fazzi, Higher-dimensional field theories from type II supergravity [arXiv:1712.04447]
-
Iñaki García Etxebarria: Symmetries from string theory talk notes (2021) [pdf]
-
Michele Del Zotto: Uncharted Territories in Geometric Engineering, talk at Strings and Geometry 2023 (2023) [slides:pdf, pdf, video:YT]
Further developments:
-
Balázs Szendrői: Nekrasov’s Partition Function and Refined Donaldson-Thomas Theory: the Rank One Case, SIGMA 8 (2012) 088 [doi:10.3842/SIGMA.2012.088, mathnet:765)
-
David Berenstein: Reverse geometric engineering of singularities, JHEP 0204 (2002) 052 [arXiv:hep-th/0201093, doi:10.1088/1126-6708/2002/04/052]
Specifically in M-theory:
-
A. Belhaj, L. B. Drissi, J. Rasmussen: On gauge models from geometric engineering in M-theory, Class. Quant. Grav. 20 (2003) 4973-4982 [arXiv:hep-th/0304019, doi:10.1088/0264-9381/20/23/002]
-
Jacob L. Bourjaily, Sam Espahbodi: Geometrically Engineerable Chiral Matter in M-Theory [arXiv:0804.1132, spire:782985]
-
Jacob L. Bourjaily: Multiple unfoldings of orbifold singularities: Engineering geometric analogies to unification, Phys. Rev. D 79 (2009) 046005 [doi:10.1103/PhysRevD.79.046005, arXiv:0704.0444]
-
Jacob L. Bourjaily: Local Models in F-Theory and M-Theory with Three Generations [arXiv:0901.3785, spire:811744]
-
Andrea Sangiovanni: M-theory geometric engineering for 5d SCFTs and Gopakumar-Vafa invariants, PhD thesis, Trieste (2022) [inSpire:2181479, hdl:11368/3030926]
-
Andrea Sangiovanni, Roberto Valandro: M-theory geometric engineering for rank-0 3d theories [arXiv:2410.13943]
Cast in “generalized symmetry” language:
-
Michele Del Zotto, Shani Nadir Meynet, Robert Moscrop: Remarks on Geometric Engineering, Symmetry TFTs and Anomalies [arXiv:2503.19022]
-
Mario De Marco, Shani Nadir Meynet: Symmetries Beyond Branes: Geometric Engineering and Isometries [arXiv:2503.19022]
Examples
Geometric engineering of SCFT
For geometric engineering of the D=6 N=(2,0) SCFT, see at duality between M-theory on Z2-orbifolds and type IIB string theory on K3-fibrations – Geometric engineering of 6d (2,0)-SCFT.
Geometric engineering of SCFT
On D=6 N=(1,0) SCFTs via geometric engineering on M5-branes/NS5-branes at D-, E-type ADE-singularities, notably from M-theory on S1/G_HW times H/G_ADE, hence from orbifolds of type I' string theory (see at half NS5-brane):
-
Michele Del Zotto, Jonathan Heckman, Alessandro Tomasiello, Cumrun Vafa, 6d Conformal Matter, JHEP02(2015)054 (arXiv:1407.6359)
-
Davide Gaiotto, Alessandro Tomasiello, Holography for theories in six dimensions, JHEP12(2014)003 (arXiv:1404.0711)
-
Kantaro Ohmori, Hiroyuki Shimizu, Compactifications of 6d Theories and Brane Webs, J. High Energ. Phys. (2016) 2016: 24 (arXiv:1509.03195)
-
Hirotaka Hayashi, Sung-Soo Kim, Kimyeong Lee, Futoshi Yagi, 6d SCFTs, 5d Dualities and Tao Web Diagrams, JHEP05 (2019)203 (arXiv:1509.03300)
-
Ibrahima Bah, Achilleas Passias, Alessandro Tomasiello, compactifications with punctures in massive IIA supergravity, JHEP11 (2017)050 (arXiv:1704.07389)
Engineering of topological order on M5s
Claim of geometric engineering of topological order on M5-branes
on coincident branes by assuming the SCFT:
-
Gil Young Cho, Dongmin Gang, Hee-Cheol Kim: M-theoretic Genesis of Topological Phases, J. High Energ. Phys. 2020 115 (2020) [arXiv:2007.01532, doi:10.1007/JHEP11(2020)115]
-
Shawn X. Cui, Yang Qiu, Zhenghan Wang, From Three Dimensional Manifolds to Modular Tensor Categories, Commun. Math. Phys. 397 (2023) 1191–1235 [doi:10.1007/s00220-022-04517-4, arXiv:2101.01674]
-
Federico Bonetti, Sakura Schäfer-Nameki, Jingxiang Wu: : 3d Topological Order Labeled by Seifert Manifolds [arXiv:2403.03973]
on single M5 probe branes by taking into account proper flux-quantization:
Last revised on July 4, 2025 at 07:25:45. See the history of this page for a list of all contributions to it.