nLab phase space
Context
Variational calculus
Differential geometric version
Derived differential geometric version
Physics
physics, mathematical physics, philosophy of physics
Surveys, textbooks and lecture notes
theory (physics), model (physics)
experiment, measurement, computable physics
-
-
-
Axiomatizations
-
Tools
-
Structural phenomena
-
Types of quantum field thories
-
Contents
Idea
The covariant phase space of a system in physics (a field theory, in general) is
-
the space of all of those fields on spacetime which solve the equations of motion, hence
-
the space of on-shell field histories, hence
-
the space of trajectories of the system.
Often one considers a parameterization of this by initial value data of fields on a Cauchy surface inside spacetime. This parameterization is what traditionally is just called a “phase space”, or canonical phase space, for emphasis. Its elements are typically described by
-
“canonical coordinates”: the value of the fields themselves, on the Cauchy surface
-
“canonical momenta”: essentially the temporal derivatives of the fields, on the Cauchy surface.
The “covariant” in “covariant phase space” is to indicate that it is obtained without any (necessarily un-natural, hence in physics jargon: non-covariant) choices of foliation of spacetime by Cauchy surfaces. But if a canonical phase space exists, then time evolution of initial value data is an isomorphism from the “canonical” to the “covariant” phase space.
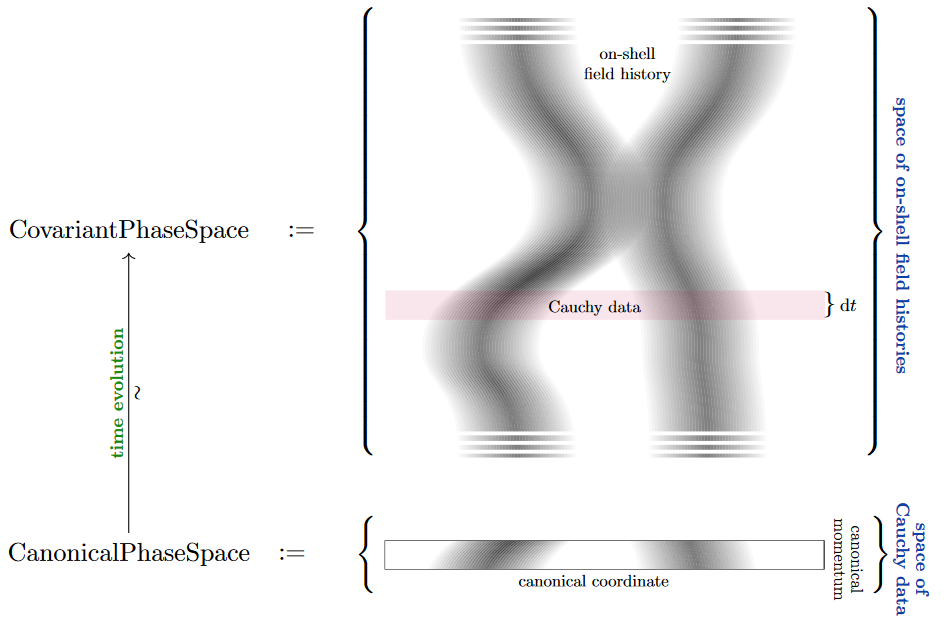
For a system described by Lagrangian mechanics, the covariant phase space comes canonically equipped with a presymplectic structure. A proper phase space or reduced phase space is a quotient space of the covariant phase space on which the presymplectic structure refines to a symplectic structure or Poisson strucure.
Typically these phase spaces are (locally) naturally parameterized by the suitable boundary conditions which uniquely determine the corresponding history of the physical system. Much of the literature on phase spaces deals with parameterizing these boundary conditions.
For instance for a non-relativistic particle propagating on a Riemannian manifold with the usual action functional, a trajectory is uniquely fixed by the position and the momentum of the particle at a given time. Correspondingly the space of all solutions and hence the (covariant) phase space of the system may be identified with the cotangent bundle of .
(The term “phase” in “phase space” can be related to the phase of complex numbers in this example, see at phase and phase space in physics.)
However, even reduced phase spaces are not all cotangent bundles, typically not, for instance, if they are obtained by symplectic reduction. This way a finite-dimensional phase space can sometimes describe continuous systems (e.g. in hydrodynamics) whch have infinitely many degrees of freedom; that phase space is however not a cotangent bundle of something in general.
Covariant phase space
There are two main routes to the construction of the covariant phase space,
-
(S) via presymplectic structure;
-
(P) via Poisson algebra structure.
(S) Via pre-symplectic structures
We describe the canonical presymplectic structure on the covariant phase space of a local action functional. The covariant phase space is defined as the space of critical points of an action functional or, equivalently, the space of solutions of its Euler-Lagrange equations, also known as the shell. The shell is naturally embedded as a subset of the space of all field configurations. Below, terminology and notation are as in the discussion at variational bicomplex.
Let be a smooth fiber bundle over an -dimensional spacetime and the corresponding jet bundle. The total de Rham differential on decomposes, , into the anti-commuting horizontal and vertical differentials, and . The local action functional
is by definition given by a Lagrangian
as
The variation of the action can be written in terms of the vertical differential:
where the first the variational differential (as interpreted in the bicomplex definition) and the second is the vertical differential. Thus, for the purposes of variational calculus, we can concentrate purely on the vertical differential of the Lagrangian, which canonically decomposes as follows:
where is the Euler-Lagrange equation on , and where is a degree- and is a degree- element in the variational bicomplex (one variational form degree and, respectively, or -spacetime form degrees).
Remark
On a local coordinate patch for the form here is given by
If is the sum of a standard kinetic Lagrangian for a free field theory and a potential term that only depends on the fields themselves and not on their derivatives, then this is at the same time the canonical multisymplectic form for the given field bundle. See at multisymplectic geometry the section Examples – Free field theory for more on this relation.
The above definition of and in terms of yields the following identity upon taking another exterior variational derivative of both sides
where the first term on the right clearly vanishes when pulled back to the shell, on . The above wedge product between variational forms is inherited from the wedge product on . This implies that the presymplectic current, , is horizontally closed on shell:
where is the embedding of the solutions of the Euler-Lagrange equations (the shell) into the space of all field configurations. The reason is that for each , since the functions are all constant (in fact ) on solutions.
The variational 1-form on the space of field configurations
given by an integration over a Cauchy surface is the potential for the presymplectic form
on the space of field configurations. Since is horizontally closed on shell, the the pullback of the presymplectic form is independent of the choice of the surface (provided the choice is restricted to a single homology class of surfaces).
Proposition
The presymplectic form on the covariant phase space is symplectic iff the linearized Euler-Lagrange equations, , have a locally well-posed initial value problem on . In particular, in the presence of gauge symmetries, due to the failure of uniqueness of solutions for given initial data on , the form is only presymplectic.
However, the infinitesimal actions of gauge symmetries exhaust the kernel of the and upon performing symplectic reduction, we obtain the space of orbits of solutions under the action of gauge symmetries, which is the physical or reduced phase space.
Notice that the form , on the field configuration space, does depend on the choice of Cauchy surface. Performing symplectic reduction gives the symplectic space of equivalence classes of solutions of equations of motion modulo gauge transformations, and hence also the reduced phase space. Thus, the end point of the reduction no longer depends on the choice of the Cauchy surface.
Remark
Application to the inverse problem of the calculus of variations
We discuss the inverse problem of variational calculus:
given a presymplectic form on the locus of solutions of a system of partial differential equations, when is it the covariant phase space of a local action functional?
(This section follows Bridges, Hydon & Lawson.)
We use same notation as above. Namely, dependence on in local forms really means dependence on finitely many components of the infinite jet . Also, denotes the embedding of the space of solutions in the space of field configurations. Moreover, we presume to work on a sufficiently small neighborhoods in the space of solutions and field configurations that the Poincar'e lemma applies.
Consider a system of partial differential equations , together with a local presymplectic form , where is a degree- element of the variational bicomplex, that is . Suppose further that presymplectic current density is horizontally conserved on solutions:
where and are systems (suitably contracted with the system) of degree- and degree- elements of the variational bicomplex. Using the variational closure of , we can conclude that and thus, locally, . (…Justify why the representative on the last RHS can be chosen proportional to …)
On the other hand, the variational closure of also implies the existence of a degree- form , such that . The following identity then allows us to (locally) reconstruct a Lagrangian whose Euler-Lagrange equations are satisfied by solutions to .
where is a degree- form and is a Lagrangian degree- form. Rearranging the last equality as
we conclude that the Euler-Lagrange equations of are satisfied on solutions of , since .
(P) Via Poisson structures
The covariant phase space can be embedded into the space of field configurations as a subspace of the set of solutions that transversely intersects gauge orbits. This embedding is characterized as the zero locus of the equations of motion and some gauge fixing conditions. The non-degenerate Poisson structure on the algebra of functions on the covariant phase space is given by the Peierls bracket.
The Peierls bracket of two functions and is the antisymmetrized influence on of an infinitesimal perturbation of a gauge-fixed action by function that restricts to on the embedding. The algebra of functions on the space of field configurations becomes a Poisson algebra in the following way. Pick a set of functions on the space of field configurations that restrict to a non-degenerate coordinate system on the embedded covariant phase space. These functions, together with the equations of motion and gauge fixing conditions define a Poisson bivector by being declared canonical, such that the kernel of the bivector coincides with the ideal generated by the equations of motion and the gauge fixing conditions. Obviously the Poisson structure thus constructed on the algebra of functions on field configurations is not unique and depends on the above choice of coordinates; the same non-uniqueness may be parametrized instead by a choice of a connection on the space of field configurations. The embedded covariant phase space becomes a leaf of the symplectic foliation of the space of field configurations.
Via the BV-complex
The BV-BRST complex of a local action functional is (the formal dual to) a resolution of the reduced covariant phase space (the quotient of the covariant phase space by symmetries). As discussed in more detail at BV-BRST complex the ghost sector of that complex is a model for the quotient by the symmetries, whereas the antifield/antighost sector is a model for the critical locus of the action functional.
Moreover, by the nature of its construction, the BV-complex is canonically equipped with a graded symplectic form , whose (-1)-graded Poisson bracket is called the antibracket (essentially the canonical Schouten bracket on graded derivations, see at derived critical locus). This is not the canonical symplectic form on the reduced phase space, as discussed above, but it is something like a potential for it.
We want to claim the following
Proposition
Given a local action functional on a space of fields over a spacetime . Let denote the differential of the BV-BRST complex and let denote the horizontal de Rham differential on . Then
If is a globally hyperbolic spacetime of the form then this is
We discuss this now in more detail. (The stament then also appears in Cattaneo-Mnev-Reshetikhin 12, equation (9)).
Write
-
for the spacetime on which the fields are defined;
-
for the configuration space of fields on , where is some vector space (for simplicity);
-
for the BV-extension; for the corresponding graded vector space;
-
for a chosen basis of ;
-
for the functional whose value on is (for );
-
for the corresponding variational bicomplex.
-
for the antifield corresponding to (which is an antighost if is a ghost).
Then the symplectic form density for the antibracket
is
Then,
We observe that the term in parenthesis is – in the notation at derived critical locus (so we are assuming now the assumptions made there) –
Hence
where is the Euler-Lagrange density as in Zuckerman, p. 267. By equation g) there, this is
Examples
Relativistic particle
The covariant phase space of the relativistic particle on a pseudo-Riemannian manifold is the space of geodesics of (in the absence of a background gauge field).
Chern-Simons theory
For Chern-Simons theory corresponding to a non-degenerate bilienear invariant polynomial on a Lie algebra the
-
configuration space is the space of Lie algebra valued forms;
-
covariant phase space is the space of field configurations whose curvature 2-form vanishes
-
the presymplectic structure is
See Chern-Simons theory and ∞-Chern-Simons theory for more details.
In dg-geometry
(…)
Let the ambient context be that of dg-geometry. Let be an ordinary smooth manifold, assumed finite dimensional for the moment, and an ordinary smooth function such that its 0-locus is an sub-manifold.
Then a presentation for the homotopy fiber of is given by the formal dual of the dg-algebra
concentrated in non-positive degree, which in degree has the th exterior powers of the tangent vectors of and whose differential is given by contracting a tangent vector with the 1-form .
This is a Koszul resolution-type resolution of the 0-locus of . More generally, the homotopy fiber is given by a Koszul-Tate resolution-type complex. This is known as the antifield complex in the BV-BRST formulation of derived phase spaces.
(…)
Related concepts
Reductions of (pre-)symplectic manifolds:
References
A a popular introduction to the notion of phase space with some comments on the history of the concept are in
- David Nolte, The tangled tale of phase space, PhysicsToday (April 2010) [web]
Covariant phase space
Textbook account with an eye towards BRST-BV formalism:
- Marc Henneaux, Claudio Teitelboim, 17.1 in: Quantization of Gauge Systems, Princeton University Press (1992) [ISBN:9780691037691, jstor:j.ctv10crg0r]
An article reviewing much of the content of the following references:
- Igor Khavkine, Covariant phase space, constraints, gauge and the Peierls formula, International Journal of Modern Physics A 29 (2014) [arXiv:1402.1282, doi:10.1142/s0217751x14300099]
Further review:
-
L. Vitagliano, Secondary calculus and the covariant phase space [arXiv:0809.4164]
-
M. J. Gotay, J. Isenberg, R. Montgomery, J. E. Marsden, Momentum Maps and Classical Fields, Part I: Covariant Field Theory pdf
A discussion in the context of the variational bicomplex with further pointers to the use in physics is in
- E. Reyes, On Covariant Phase Space and the Variational Bicomplex , Int. J. Theor. Phys. 43, no 5 (2004) 1267-1286
A discussion in the language of D-modules, following the book Chiral Algebras and leading up to the derived covariant phase space by BRST-BV formalism is in section 8.3 of
- Frédéric Paugam, Towards the mathematics of quantum field theory (pdf)
Discussion in the context of smooth sets:
- Grigorios Giotopoulos, Hisham Sati, §7.3 in: Field Theory via Higher Geometry I: Smooth Sets of Fields [arXiv:2312.16301]
On the relation between covariant phase space methods and multisymplectic geometry:
-
Frédéric Hélein, Multisymplectic formalism and the covariant phase, in Roger B ielawski, Kevin Houston, Martin Speight, J. Martin Speight (eds.) Variational problems in differential geometry, London Mathematical Society Lecture Note Series (2012) (arXiv:1106.2086)
-
Thomas J. Bridges, Peter E. Hydon and Jeffrey K. Lawson, Multisymplectic structures and the variational bicomplex [doi]
-
Michael Forger, Sandro Romero, Covariant Poisson brackets in geometric field theory, Commun. Math. Phys. 256 (2005) 375-410 [arXiv:math-ph/0408008, doi:10.1007/s00220-005-1287-8]
Original articles on covariant phase space technology
In the following we give a commented list of references following the historical development.
It seems that there have been two independent lines of development, somewhat independent of each other, but also with some crosspollination along the way. One stream (P) was concerned with the construction of a Poisson structure on functions of solutions, while the other (S) was concerned with the construction of a symplectic form on the space of solutions. Obviously, the differences between the two kinds of constructions show up precisely in gauge theory systems.
The earliest papers are those of Peierls and Bergmann-Schiller in the early 50’s. They seem to have been self-motivated. Below, we try to list papers that have established key results or have served as important popularizers together with their main influences from previous works. The constructions of the (S) stream seem to have appeared nearly independently several times over several decades, until Lee-Wald and followups of Ashtekar’s papers became standard references. The (P) stream flowed slowly, but consistently from original idea of Peierls. The papers of Fredenhagen-Dütsch-et-al are a most readable modern formulation.
-
R. Peierls, The commutation laws of relativistic field theory (1952) (jstor)
(P)
Influence: Appears to be self-motivated. The result may have been guessed from the known unequal-time, covariant Poisson brackets between free fields, which involve the causal Green function in an explicit way.
Result: The Peierls bracket on the covariant phase pace of a non-gauge system is defined and equivalence with the Hamiltonian phase space symplectic structure is proved. Gauge systems are treated by example of electrodynamics. The solution to degenerate equations of motion is either adding gauge fixing terms to the action or consider non-degenerate equations of motion satisfied by gauge invariant fields. Fermions are handled by multiplying fermi fields by formal odd parameters.
-
Bergmann-Schiller, Classical and quantum field theories in the Lagrangian Formalism Phys. Rev. 89 4-16 (1953) (prola)
(S)
Influence: Appears to be motivated by Bergmann’s long term and “brute force” analysis of the gauge invariance structure of relativity and structurally similar theories. Another motivation is the possibility of writing divergence-less stress energy tensors as “curls” of “superpotentials”.
Result: The pre-symplectic potential form-current makes an appearance. The definitions of the covariant phase space and the resulting symplectic form on it are obscure (at least to me), but later papers make reference to them.
-
Bergmann-Goldberg-Janis-Newman, Canonical Transformations and Commutators in the Lagrangian Formalism Phys. Rev. 103, 807–813 (1956) (prola)
(P&S)
Influence: Peierls, Bergmann-Schiller
Result: Proof of the equivalence between the Peierls bracket and the bracket obtained by Bergmann-Schiller for non-gauge systems. The treatment of gauge systems and many of the calculations are maybe a bit obscure.
-
Komar, Commutators on Characteristic Surfaces Phys. Rev. 134, B1430–B1440 (1964) (proceedings w/ Bergmann 1962)
(S)
Influence: Bergmann-Schiller
Result: Uses the methods of Bergmann-Schiller to define Poisson brackets on initial data for linearized gravitational waves on null hypersurfaces, including at null infinity.
-
DeWitt B.S., DeWitt C. (eds.) Relativity, Groups, and Topology (Les Houches 1963, Gordon and Breach, 1964), pp.585-820 (1964; lecture notes 1963)
(P)
Influence: Peierls
Result: A more detailed exposition of Peierls’ idea, with a bit more generality in the treatment of gauge systems. Becomes a standard reference along with Peierls’ original paper.
-
Friedman, Generic instability of rotating relativistic stars Commun. math. Phys. 62, 247–278 (1978) (springer)
(S)
Influence: Bergmann-Schiller, Komar, … (?)
-
Ashtekar-Magnon, On the symplectic structure of general relativity Communications in Mathematical Physics Volume 86, Number 1, 55-68, DOI: 10.1007/BF01205661 (1982) (springer)
(S)
Influence: Komar, also some more obscure papers by Fridmann and Palmer
Result: Write down the explicit pre-symplectic current and the corresponding pre-symplectic form on the space of solutions of linearized gravitational wave equations. This symplectic form on the reduced space of solutions is shown to coincide with the ADM symplectic structure and with the Komar symplectic structure at null infinity. The motivation explicit pre-symplectic current formula appears from the desire to interpolate between the above two formalisms.
-
Edward Witten, §5 in: Interacting field theory of open superstrings, Nuclear Physics B 276 2 (1986) 291-324 [doi:10.1016/0550-3213(86)90298-1, inspire:228073]
(S)
Influence: Appears to be self-motivated. Witten needed a covariant way to define Poisson brackets from the action of open string field theory. Acknowledges parallel, independent work of Zuckerman.
Result: Witten writes down the pre-symplectic form-current “by inspection” for a scalar field and for a Chern-Simons theory, then he explicitly shows that the current is conserved on the space of solutions, and that its integral over a Cauchy surface is variationally closed.
-
Ashtekar, Bombelli, Koul, YS Kim, WW Zachary (eds.), The Physics of Phase Space: Nonlinear Dynamics and Chaos, Geometric Quantization, and Wigner Function (p.356) ISBN 0-387-17894-5 (1987; preprint 1986)
(S)
Influence: Ashtekar-Magnon
Result: Explicit formula for the symplectic form of full, nonlinear general relativity as an integral of a conserved form-current over an arbitrary Cauchy surface. Discussion of conversion of symmetries into conserved quantities using this form. Some of the aspects related to the construction of such conserved have apparently been treated in earlier works by Friedman, Sachs and possibly some others.
-
Gregg Zuckerman, Action Principles and Global Geometry, in Mathematical Aspects of String Theory, S. T. Yau (Ed.), World Scientific, Singapore, 1987, pp. 259-284. (pdf)
(S)
Influence: Appears to be self-motivated. Possible motivation is a more general construction of conserved currents in variational problems, a la Noether. Acknowledges that he reproduces parallel, but applied to specific theories, work of Crnković & Witten (1987) and Ashtekar-Bombelli-Koul.
Result: The construction of the pre-symplectic potential form-current and pre-symplectic form-current are given in essentially modern terms. Not all proofs are given. Little discussion of symplectic reduction.
-
Čedomir Crnković, Edward Witten, Covariant Description of Canonical Formalism in Geometrical Theories, chapter 16 in: S. W. Hawking and W. Israel (eds.) Three Hundred Years of Gravitation, Cambridge University Press (1987) 676-684 [pdf, ISBN:9780521379762]
(S)
Influence: Witten
Result: Applies the “by inspection” methods of Witten’s earlier paper to write down conserved, variationally-closed pre-symplectic currents for Yang-Mills and general relativity.
-
Čedomir Crnković, Symplectic Geometry of the Covariant Phase Space, Class. Quant. Grav. 5 (1988) 1557-1575 [doi:10.1088/0264-9381/5/12/008, inspire:247290]
-
J. Lee, Robert Wald, Local symmetries and constraints (1989) J. Math. Phys. 31, 725 (1990); doi:10.1063/1.528801 (jMP)
(S)
Influence: Crnković-Witten, Friedman
Result: Essentially gives the modern formulation as described above. The exposition is quite similar to Zuckerman (though no connection with that work is made), but with complete proofs.
-
Ashtekar-Bombelli-Reula, The Covariant Phase Space of Asymptotically Flat Gravitational Fields in Mechanics, Analysis and Geometry: 200 Years after Lagrange edited by M. Francaviglia and D.~Holm, North-Holland, Amsterdam, 1990. (web)
(S)
Influence: Ashtekar-…
Result: Becomes standard reference. (?)
-
Poisson Brackets on the Space of Histories Annals of Physics Volume 236, Issue 2, December 1994, Pages 374-391
(arXiv:hep-th/9308141)The generalized Peierls bracket (arXiv:hep-th/9308150)
(1994; preprints 1993, thesis 1992)
(P)
Influence: Peierls, DeWitt; mentions but does not use the material from Lee-Wald, Crnkovic-Witten, Ashtekar
Result: Gives the construction outlined above.
-
Stefan Hollands, Donald Marolf, Asymptotic generators of fermionic charges and boundary conditions preserving supersymmetry (arXiv) (2007, preprint 2006)
(S)
Influence: Lee-Wald
Result: Extends analysis to classical fermi fields.
-
Dütsch Klaus Fredenhagen, The Master Ward Identity and Generalized Schwinger-Dyson Equation in Classical Field Theory (arXiv:hep-th/0211242) (2003),
Brennecke-Duetsch, Removal of violations of the Master Ward Identity in perturbative QFT (2008) (arXiv:0705.3160),
Rejzner, Fermionic fields in the functional approach to classical field theory (2011) (arXiv:1101.5126)
(P)
Influence: Peierls, DeWitt, Marolf; also some ideas related to retarded products that go back to Glaser-Lehmann-Zimmermann in the 1950s (more precisely: Glaser, V., Lehmann, H. and Zimmermann, W., “Field Operators and Retarded Functions” Nuovo Cimen. 6 (1957) 1122)
Result: Modern, elementary treatment of the Peierls bracket, including for classical fermi fields. The discussion is simplified by sticking to non-degenerate (or gauge fixed) actions. The choice of coordinates on the space of field configurations is simplified by considering only vector bundle valued fields.
A different but related approach is
- Jerzy Kijowski, Wlodzimierz M. Tulczyjew, A Symplectic Framework for Field Theories, Lecture Notes in Physics 107 (1979, 2005) [doi:10.1007/3-540-09538-1]
also discussed (with focus on application to gravity) in:
- Alberto S. Cattaneo, Phase space for gravity with boundaries, Encyclopedia of Mathematical Physics (2023) [arXiv:2307.04666]
for the case of manifolds with boundary:
-
Daniel Harlow, Jie-qiang Wu, Covariant phase space with boundaries, J. High Energ. Phys. 2020 146 (2020). [arXiv:1906.08616, doi:10.1007/JHEP10(2020)146]
-
Juan Margalef-Bentabol, Eduardo J. S. Villaseñor, Geometric formulation of the covariant phase space methods with boundaries, Phys. Rev. D 103 (2021) 025011 [doi:10.1103/PhysRevD.103.025011, arXiv]
-
Valle Varo, The Covariant Phase Space of Gravity with Boundaries [arXiv:2301.12418]
-
Alejandro Corichi, Juan D. Reyes, Tatjana Vukasinac, On covariant and canonical Hamiltonian formalisms for gauge theories [arXiv:2312.10229]]
See also:
- Vinícius Bernardes, Theodore Erler, Atakan Hilmi Fırat: Covariant phase space and algebras [arXiv:2506.20706]
Reduced phase space
Standard textbooks on classical mechanics include
-
Vladimir Arnold, Mathematical methods of classical mechanics
-
H. Goldstein, Classical mechanics
-
L. D. Landau, E. M. Lifshitz, Mechanics, (vol. I of Landau-Lifschitz Course on theoretical physics)
-
R. Abraham, J. E. Marsden, Foundations of mechanics
-
J. E. Marsden, T. Ratiu, Introduction to mechanics and symmetry
-
wikipedia: phase space
BV formalism
Discussion via BV-formalism includes
- Alberto Cattaneo, Pavel Mnev, Nicolai Reshetikhin, Classical BV theories on manifolds with boundary (arXiv:1201.0290)
Last revised on June 27, 2025 at 06:04:23. See the history of this page for a list of all contributions to it.