nLab Dynkin diagram
under construction
Context
Graph theory
Properties
Extra properties
Extra structure
Representation theory
geometric representation theory
Ingredients
Definitions
representation, 2-representation, ∞-representation
Geometric representation theory
-
Grothendieck group, lambda-ring, symmetric function, formal group
-
principal bundle, torsor, vector bundle, Atiyah Lie algebroid
-
Eilenberg-Moore category, algebra over an operad, actegory, crossed module
Theorems
Contents
Idea
A Dynkin diagram is a labeled graph that possesses a one-to-one correspondence with a finite indecomposable reduced root system, thus with a simple complex finite dimensional Lie algebra or Cartan matrix?.
The construction of a Dynkin diagram from the Cartan Matrix?, is obtained from the following procedure:
-
Number of vertices = Number of simple roots = size of = n
-
If then are connected by a nonlabeled edge.
-
If and then are connected by arrows labeled by <.
Properties
Classification of simple Lie groups
classification of simple Lie groups:
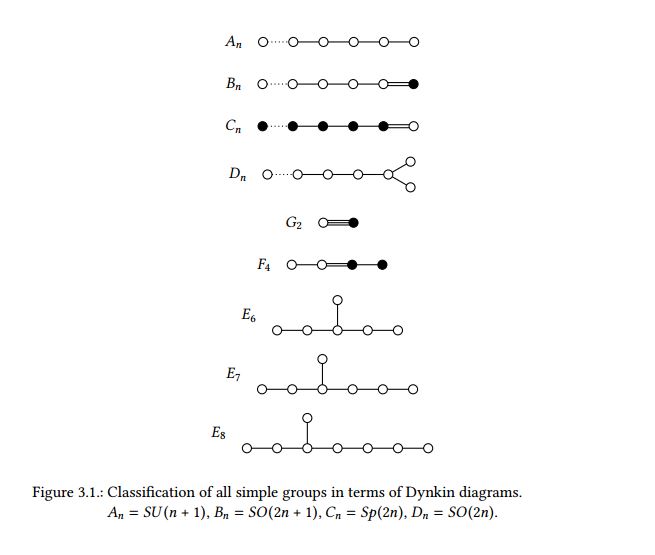
graphics grabbed from Schwichtenberg
ADE-Classification
Those Dynkin diagrams in the ADE classification are the following
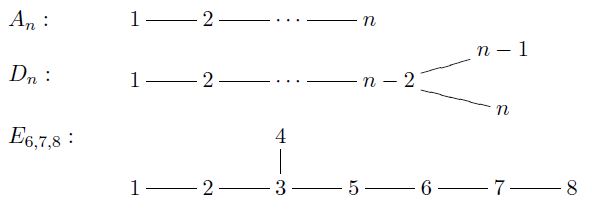
ADE classification and McKay correspondence
Dynkin Index
Let be a finite simple complex Lie algebra with a Killing form on given by the trace in the adjoint representation, for .
For any irreducible finite representation of , Where is the Dynkin Index of .
The Dynkin index can also be defined in terms of the eigenvalue of the quadratic Casimir operator: .
Remark
In mathematical physics,in the context of embeddings of gauge fields, the Dynkin index is used in the calculation of topological charges (instanton number). To demonstrate this, let be a gauge potential on the Euclidean space given by
where are the generators of a compact gauge group . If the gauge field is an embedding of in then the Dynkin index of the embedding is denoted as . The topological charge is
where is the charge of treated as a gauge field. The proof was carried out for by Bitar and Sorba see Myers, de Roo & Sorba 79, Sec. 2, which can be extended to arbitrary simple compact groups.
Related concepts
References
General
Named after Eugene B. Dynkin.
See also:
- Wikipedia, Dynkin diagram
Dynkin index
-
Bianchi M. et al. (2004) Dynkin Index. In: Duplij S., Siegel W., Bagger J. (eds) Concise Encyclopedia of Supersymmetry. Springer, Dordrecht. publisher
-
C. Meyers, Mees de Roo, P. Sorba, Group-theoretical aspects of instantons. Nuov Cim A 52, 519–530 (1979) (doi:10.1007/BF02770858)
Last revised on September 2, 2024 at 10:53:34. See the history of this page for a list of all contributions to it.