nLab type of booleans

 Idea

The boolean domain in dependent type theory.

Definition

The type of booleans, denoted $\mathrm{Bool}$, $\mathbb{2}$, or $\mathbf{2}$, can be defined in a dependent type theory in many different ways:

• as a positive inductive type representing the homotopy-initial type with two elements.

• as the type of decidable propositions, itself defined in multiple different ways

• as the 0-sphere type, the suspension type of the empty type

As an inductive type

Assuming that identification types and dependent product types exist in the type theory, the type of booleans is the inductive type generated by two elements, and is defined by the following inference rules:

type formation rules for the type of booleans

$$\frac{\Gamma \; \mathrm{ctx}}{\Gamma \vdash \mathrm{Bool} \; \mathrm{type}}$$

term introduction rules for the type of booleans:

$$\frac{\Gamma \; \mathrm{ctx}}{\vdash 0:\mathrm{Bool}} \qquad \frac{\Gamma \; \mathrm{ctx}}{\Gamma \vdash 1:\mathrm{Bool}}$$

term elimination rules for the type of booleans:

$$\frac{\Gamma, x:\mathrm{Bool} \vdash C(x) \; \mathrm{type}}{\Gamma, c_0:C(0), c_1:C(1), p:\mathrm{Bool} \vdash \mathrm{ind}_\mathrm{Bool}^C(c_0, c_1, p):C(p)}$$

computation rules for the type of booleans:

• judgmental computation rules

  $$\frac{\Gamma, x:\mathrm{Bool} \vdash C(x) \; \mathrm{type}}{\Gamma, c_0:C(0), c_1:C(1) \vdash \mathrm{ind}_\mathrm{Bool}^C(c_0, c_1, 0) \equiv c_0:C(0)}$$
  $$\frac{\Gamma, x:\mathrm{Bool} \vdash C(x) \; \mathrm{type}}{\Gamma, c_0:C(0), c_1:C(1) \vdash \mathrm{ind}_\mathrm{Bool}^C(c_0, c_1, 1) \equiv c_1:C(1)}$$

• typal computation rules

  $$\frac{\Gamma, x:\mathrm{Bool} \vdash C(x) \; \mathrm{type}}{\Gamma, c_0:C(0), c_1:C(1) \vdash \beta_\mathrm{Bool}^0(c_0, c_1):\mathrm{Id}_{C(0)}(\mathrm{ind}_\mathrm{Bool}^C(c_0, c_1, 0), c_0)}$$
  $$\frac{\Gamma, x:\mathrm{Bool} \vdash C(x) \; \mathrm{type}}{\Gamma, c_0:C(0), c_1:C(1) \vdash \beta_\mathrm{Bool}^1(c_0, c_1, 1):\mathrm{Id}_{C(1)}(\mathrm{ind}_\mathrm{Bool}^C(c_0, c_1, 1), c_1)}$$

uniqueness rules for the type of booleans:

• judgmental uniqueness rules
  $$\frac{\Gamma, x:\mathrm{Bool} \vdash C(x) \; \mathrm{type}}{\Gamma, c:\prod_{x:\mathrm{Bool}} C(x), p:\mathrm{Bool} \vdash \mathrm{ind}_\mathrm{Bool}^C(c(0), c(1), p) \equiv c(p):C(p)}$$
• typal uniqueness rules
  $$\frac{\Gamma, x:\mathrm{Bool} \vdash C(x) \; \mathrm{type}}{\Gamma, c:\prod_{x:\mathrm{Bool}} C(x), p:\mathrm{Bool} \vdash \eta_\mathrm{Bool}(c, p):\mathrm{Id}_{C(p)}(\mathrm{ind}_\mathrm{Bool}^C(c(0), c(1), p), c(p))}$$

The elimination, typal computation, and typal uniqueness rules for the type of booleans state that the type of booleans satisfies the dependent universal property of the type of booleans. If the dependent type theory also has dependent sum types and product types, allowing one to define the uniqueness quantifier, the dependent universal property of the type of booleans can be simplified to the following rule:

$$\frac{\Gamma, x:\mathrm{Bool} \vdash C(x) \; \mathrm{type}}{\Gamma, c_0:C(0), c_1:C(1)\vdash \mathrm{up}_\mathrm{Bool}^C(c_0, c_1):\exists!c:\prod_{x:\mathrm{Bool}} C(x).\mathrm{Id}_{C(0)}(c(0), c_0) \times \mathrm{Id}_{C(1)}(c(1), c_1)}$$

The judgmental computation and uniqueness rules imply the typal computation and uniqueness rules and thus imply the dependent universal property of the type of booleans.

In type theories with a separate type judgment where not all types are elements of universes, one has to additionally add the following elimination and computation rules:

Elimination rules:

$$\frac{\Gamma \vdash A \; \mathrm{type} \quad \Gamma \vdash B \; \mathrm{type}}{\Gamma, x:\mathrm{Bool} \vdash \mathrm{typerec}_{\mathrm{Bool}}^{A, B}(x) \; \mathrm{type}}$$

Computation rules:

• judgmental computation rules

$$\frac{\Gamma \vdash A \; \mathrm{type} \quad \Gamma \vdash B \; \mathrm{type}}{\Gamma \vdash \mathrm{typerec}_{\mathrm{Bool}}^{A, B}(0) \equiv A \; \mathrm{type}}$$

$$\frac{\Gamma \vdash A \; \mathrm{type} \quad \Gamma \vdash B \; \mathrm{type}}{\Gamma \vdash \mathrm{typerec}_{\mathrm{Bool}}^{A, B}(1) \equiv B \; \mathrm{type}}$$

• typal computation rules

$$\frac{\Gamma \vdash A \; \mathrm{type} \quad \Gamma \vdash B \; \mathrm{type}}{\Gamma \vdash \beta_{\mathrm{Bool}}^{0, A, B}:\mathrm{typerec}_{\mathrm{Bool}}^{A, B}(0) \simeq A}$$

$$\frac{\Gamma \vdash A \; \mathrm{type} \quad \Gamma \vdash B \; \mathrm{type}}{\Gamma \vdash \beta_{\mathrm{Bool}}^{1, A, B}:\mathrm{typerec}_{\mathrm{Bool}}^{A, B}(1) \simeq B}$$

As the type of decidable propositions

The type of booleans can also be defined as the type of all decidable propositions, provided one already has disjunctions and the negations defined in the type theory:

• using the type of all propositions, as the subuniverse of decidable propositions.

• as a homotopy-terminal univalent type family of decidable propositions, suitably defined.

• as a type universe, with inference rules that mimic that of the negative dependent sum type $\sum_{P:U} \mathrm{isProp}(P) \times \mathrm{isDecidable}(P)$ or $\sum_{P:U} \mathrm{isProp}(T(P)) \times \mathrm{isDecidable}(T(P))$ respectively, but for all types, not just the $U$-small types.

Using the type of all propositions

Suppose that we have a type of propositions $\mathrm{Prop}$. Then, the type of booleans is defined as

$$\mathrm{Bool} \equiv \sum_{P:\mathrm{Prop}} P \vee \neg P$$

where $A \vee B$ is the disjunction of two types $A$ and $B$ and $\neg A \equiv A \to \emptyset$ is the negation of the type $A$. Both disjunctions and the empty set can be directly defined from $\mathrm{Prop}$, dependent function types, and product types.

As a homotopy-terminal type

A univalent family of decidable propositions consists of a type $A$ and a type family $(B(x))_{x:A}$ such that

• $B(x)$ is a decidable proposition for all $x:A$,

• the transport function

  $$\mathrm{tr}^B(x, y):x =_A y \to (B(x) \simeq B(y))$$

  is an equivalence of types for all $x:A$ and $y:A$

A morphism of univalent families of decidable propositions between univalent families of decidable propositions $(A, B)$ and $(A', B')$ consists of a function $f_A:A \to A'$ and a family of functions $f_B(x):B(x) \to B'(f_A(x))$.

The type of booleans $(\mathrm{Bool}, \mathrm{El})$ is the homotopy-terminal univalent family of decidable propositions: given any other univalent family of decidable propositions $(A, B)$, there exists a unique function $u_A:A \to \mathrm{Bool}$ and a unique family of functions $u_B(x):B(x) \to \mathrm{El}(u_A(x))$.

As a type universe

The type of booleans $\mathrm{Bool}$ is a type universe of all decidable propositions. It behaves as a record type where one of the fields is a type, consisting of

• a type $A \; \mathrm{type}$

• a witness $p:\mathrm{isProp}(A) \times (A \vee \neg A)$ that $A$ is a decidable proposition.

Similar to other type universes and record types with type fields, the type of booleans can be presented a la Tarski or a la Russell

A la Tarski

The type of booleans a la Tarski is given by the following natural deduction inference rules:

Formation rules for the type of booleans:

$$\frac{\Gamma \; \mathrm{ctx}}{\Gamma \vdash \mathrm{Bool} \; \mathrm{type}}$$

Introduction rules for the type of booleans:

$$\frac{\Gamma \vdash A \; \mathrm{type}}{\Gamma \vdash \mathrm{toBool}_A:\mathrm{isProp}(A) \to (A \vee \neg A) \to \mathrm{Bool}}$$

Elimination rules for the type of booleans:

$$\frac{\Gamma \vdash A:\mathrm{Bool}}{\Gamma \vdash \mathrm{El}(A) \; \mathrm{type}} \qquad \frac{\Gamma \vdash A:\mathrm{Bool}}{\Gamma \vdash \mathrm{proptrunc}(A):\mathrm{isProp}(\mathrm{El}(A))} \qquad \frac{\Gamma \vdash A:\mathrm{Bool}}{\Gamma \vdash \mathrm{lem}(A):\mathrm{El}(A) \vee \neg \mathrm{El}(A)}$$

Computation rules for the type of booleans:

$$\frac{\Gamma \vdash A \; \mathrm{type} \quad \Gamma \vdash p:\mathrm{isProp}(A) \quad \Gamma \vdash q:A \vee \neg A}{\Gamma \vdash \mathrm{El}(\mathrm{toBool}_A(p)(q)) \equiv A \; \mathrm{type}}$$

$$\frac{\Gamma \vdash A \; \mathrm{type} \quad \Gamma \vdash p:\mathrm{isProp}(A) \quad \Gamma \vdash q:A \vee \neg A}{\Gamma \vdash \mathrm{proptrunc}(\mathrm{toBool}_A(p)(q)) \equiv p:\mathrm{isProp}(A)}$$

$$\frac{\Gamma \vdash A \; \mathrm{type} \quad \Gamma \vdash p:\mathrm{isProp}(A) \quad \Gamma \vdash q:A \vee \neg A}{\Gamma \vdash \mathrm{lem}(\mathrm{toBool}_A(p)(q)) \equiv q:A \vee \neg A}$$

Uniqueness rules for the type of booleans:

$$\frac{\Gamma \vdash A:\mathrm{Bool}}{\Gamma \vdash \mathrm{toBool}_{\mathrm{El}(A)}(\mathrm{proptrunc}(A))(\mathrm{lem}(A)) \equiv A:\mathrm{Bool}}$$

Extensionality principle for the type of booleans:

$$\frac{\Gamma \vdash A:\mathrm{Bool} \quad \Gamma \vdash B:\mathrm{Bool}} {\Gamma \vdash \mathrm{ext}_\mathrm{Bool}(A, B):\mathrm{isEquiv}(\mathrm{transport}^\mathrm{El}(A, B))}$$

A la Russell

The type of all propositions a la Russell is given by the following natural deduction inference rules:

Formation rules for the type of booleans:

$$\frac{\Gamma \; \mathrm{ctx}}{\Gamma \vdash \mathrm{Bool} \; \mathrm{type}}$$

Introduction rules for the type of booleans:

$$\frac{\Gamma \vdash A \; \mathrm{type}}{\Gamma \vdash \mathrm{toBool}_A:\mathrm{isProp}(A) \to (A \vee \neg A) \to \mathrm{Bool}}$$

Elimination rules for the type of booleans:

$$\frac{\Gamma \vdash A:\mathrm{Bool}}{\Gamma \vdash A \; \mathrm{type}} \qquad \frac{\Gamma \vdash A:\mathrm{Bool}}{\Gamma \vdash \mathrm{proptrunc}(A):\mathrm{isProp}(A)} \qquad \frac{\Gamma \vdash A:\mathrm{Bool}}{\Gamma \vdash \mathrm{lem}(A):A \vee \neg A}$$

Computation rules for the type of booleans:

$$\frac{\Gamma \vdash A \; \mathrm{type} \quad \Gamma \vdash p:\mathrm{isProp}(A) \quad \Gamma \vdash q:A \vee \neg A}{\Gamma \vdash \mathrm{toBool}_A(p)(q) \equiv A \; \mathrm{type}}$$

$$\frac{\Gamma \vdash A \; \mathrm{type} \quad \Gamma \vdash p:\mathrm{isProp}(A) \quad \Gamma \vdash q:A \vee \neg A}{\Gamma \vdash \mathrm{proptrunc}(\mathrm{toBool}_A(p)(q)) \equiv p:\mathrm{isProp}(A)}$$

$$\frac{\Gamma \vdash A \; \mathrm{type} \quad \Gamma \vdash p:\mathrm{isProp}(A) \quad \Gamma \vdash q:A \vee \neg A}{\Gamma \vdash \mathrm{lem}(\mathrm{toBool}_A(p)(q)) \equiv q:A \vee \neg A}$$

Uniqueness rules for the type of booleans:

$$\frac{\Gamma \vdash A:\mathrm{Bool}}{\Gamma \vdash \mathrm{toBool}_{A}(\mathrm{proptrunc}(A))(\mathrm{lem}(A)) \equiv A:\mathrm{Bool}}$$

Extensionality principle for the type of booleans:

$$\frac{\Gamma \vdash A:\mathrm{Bool} \quad \Gamma \vdash B:\mathrm{Bool}} {\Gamma \vdash \mathrm{ext}_\mathrm{Bool}(A, B):\mathrm{isEquiv}(\mathrm{idToEquiv}(A, B))}$$

As the 0-sphere type

In dependent type theory with pushout types, the type of booleans / bits can be defiend as the sphere type of the 0-sphere and as such as the beginning of the suspension type-tower of types of “higher homotopy bits” — the $n$-sphere types:

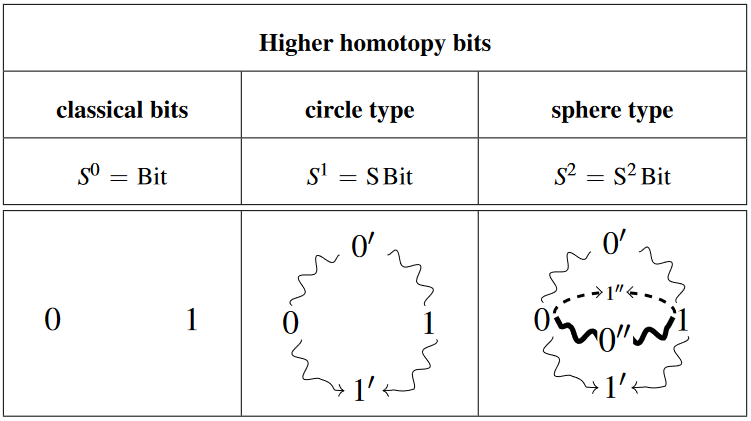
Properties

Descent and large recursion

The descent for the type of booleans states that given any types $A$ and $B$ one can construct a type family $x:\mathbb{2} \vdash \mathrm{descFam}_\mathbb{2}^{A, B}(x)$ with equivalences of types

$$\mathrm{descEquiv}_A:\mathrm{descFam}_\mathbb{2}^{A, B}(0) \simeq A \quad \mathrm{and} \quad \mathrm{descEquiv}_B:\mathrm{descFam}_\mathbb{2}^{A, B}(1) \simeq B$$

Large recursion for the type of booleans strengthens the equivalences of types in descent to judgmental equality of types

$$\mathrm{descFam}_\mathbb{2}^{A, B}(0) \equiv A \quad \mathrm{and} \quad \mathrm{descFam}_\mathbb{2}^{A, B}(1) \equiv B$$

If one is working in a dependent type theory with type variables which has identity types between types, then one can also use identifications of types instead of equivalences of types to express large recursion of the type of booleans:

$$\mathrm{descId}_A:\mathrm{descFam}_\mathbb{2}^{A, B}(0) = A \quad \mathrm{and} \quad \mathrm{descId}_B:\mathrm{descFam}_\mathbb{2}^{A, B}(1) = B$$

Extensionality principle of the type of booleans

The elements of the type of booleans represent certain truth values or propositions, namely, true and false. By the principle of propositions as some types, truth values or propositions are represented as certain types: specifically, true or $1$ is represented by the unit type $\mathbb{1}$, and false or $0$ is represented by the empty type $\mathbb{0}$. The type of booleans is a Tarski universe through the following type family:

$$x:\mathrm{Bool} \vdash \mathrm{El}(x) \coloneqq (x =_\mathrm{Bool} 1) \times \neg (x =_\mathrm{Bool} 0)$$

The extensionality principle of the type of booleans is then given by the univalence axiom:

$$\frac{\Gamma \; \mathrm{ctx}}{\Gamma, x:\mathrm{Bool}, y:\mathrm{Bool} \vdash \mathrm{ua}(x, y):\mathrm{Id}_\mathrm{Bool}(x, y) \simeq (\mathrm{El}(x) \simeq \mathrm{El}(y))}$$

Since the empty type is not equivalent to the unit type, this automatically implies that $0$ is not equal to $1$. The extensionality principle of the type of booleans can be proven from descent of the type of booleans, see Sattler 2023 for a proof.

Relation to sum types

The sum types can be defined in terms of the type of booleans and the dependent sum type. Given types $A$ and $B$, the sum type $A + B$ is defined as

$$A + B \coloneqq \sum_{x:\mathrm{Bool}} ((x =_\mathrm{Bool} 1) \to A) \times ((x =_\mathrm{Bool} 0) \to B)$$

Boolean logic

One could recursively define the logical functions on $\mathrm{Bool}$ as follows

• For negation $\neg$
  • $\neg 0 := 1$
  • $\neg 1 := 0$
• For conjunction $\wedge$
  • $0 \wedge a := 0$
  • $1 \wedge a := a$
• For disjunction $\vee$
  • $0 \vee a := a$
  • $1 \vee a := 1$
• For implication $\implies$
  • $0 \implies a := 1$
  • $1 \implies a := a$
• For the biconditional $\iff$
  • $0 \iff a := \neg a$
  • $1 \iff a := a$

One could prove that $(\mathrm{Bool}, 0, 1, \neg, \wedge, \vee, \implies)$ form a Boolean algebra. The poset structure is given by implication.

One could also inductively define observational equality on the booleans $\mathrm{Eq}_\mathrm{Bool}(x, y)$ as an indexed inductive type on the boolean type $\mathrm{Bool}$ with the following constructors

$$\mathrm{eq}_0: \mathrm{Eq}_\mathbb{2}(0, 0)$$

$$\mathrm{eq}_1: \mathrm{Eq}_\mathbb{2}(1, 1)$$

A boolean predicate valued in a type $T$ is a function $P: T \rightarrow \mathrm{Bool}$, and the type $T \to \mathrm{Bool}$ is a boolean function algebra for finite types $T$, and if path types exist, for all types $T$. Thus the functor $F: U \to BoolAlg$, $F(T) = T \to \mathrm{Bool}$ for a type universe $U$ is a Boolean hyperdoctrine, and one could do classical first-order logic inside $U$ if $\mathrm{Bool}$ and path types exist in $U$.

In fact, just with dependent sum types, dependent product types, empty type, unit type, and the two-valued type in a type universe $U$, any two-valued logic could be done inside $U$. Furthermore, since binary disjoint coproducts exist when $\mathrm{Bool}$ exists, all finite types exist in $U$, and any finitely-valued logic?, such as the internal logic of a finite cartesian power of Set, could be done inside $U$.

For finite types, one could also inductively define specific functions

$$\forall a \in A.(-)(a):(A \to \mathrm{Bool}) \to \mathrm{Bool}$$

$$\exists a \in A.(-)(a):(A \to \mathbf{2}) \to \mathrm{Bool}$$

from the type of boolean predicates on $A$ and $\mathrm{Bool}$ such that they behave like existential quantification and universal quantification.

Other properties

• The type of booleans is the suspension type of the empty type, and the suspension of the type of booleans is the circle type. Geometrically, the type of booleans is a zero-dimensional sphere.

• The type of booleans is homotopy equivalent to the type of decidable propositions in a universe $\mathcal{U}$.

$$\mathrm{Bool} \cong \sum_{P:\mathcal{U}} isProp(P) \times isDecidable(P)$$

As a result, sometimes the type of booleans is called a decidable subtype classifier.

 Related concepts

• decidable equality

• type of propositions

• boolean domain

References

Discussion in type theory as a simple example of an inductive type:

• Per Martin-Löf (notes by Giovanni Sambin), p. 37 of Intuitionistic type theory, Lecture notes Padua 1984, Bibliopolis, Napoli (1984) [pdf, pdf]

Discussion in homotopy type theory:

• Steve Awodey, Nicola Gambino, Kristina Sojakova, §3.1 in: Inductive types in homotopy type theory, LICS’12 (2012) 95–104 [arXiv:1201.3898, doi:10.1109/LICS.2012.21]

• Univalent Foundations Project, Homotopy Type Theory – Univalent Foundations of Mathematics (2013)

• Egbert Rijke, Exc. 4.2 (pp. 35) in: Introduction to Homotopy Type Theory (2023) [arXiv:2212.11082]

…

• Peter LeFanu Lumsdaine, Mike Shulman, Abstracting away from cell complexes, [talk slides pdf]

Large recursion and descent of the type of booleans can be found in

• Christian Sattler, David Wärn, Natural numbers from integers, LICS’24 (2024) 1–9 [arXiv:2405.18388, doi:10.1145/3661814.3662129]