nLab MO5
Context
String theory
Ingredients
Critical string models
Extended objects
Topological strings
Backgrounds
Phenomenology
Contents
Idea
The MO5 (Dasgupta-Mukhil 95, Sec. 2FFurther, Witten 95, Sec. 3.3) is one of the types of BPS orientifold fixed loci in M-theory/on D=11 N=1 super-spacetime. Locally on super Minkowski spacetime it is the super-orientifold given by the global orbifold quotient by the group of order 2 which is generated by the Clifford algebra-element in the positive pin group (for precise details see HSS 18, Lemma 4.12).
Properties
Charge, anomaly cancellation and duality to O4-planes
Under duality between M-theory and type IIA string theory, for KK-compactification along a circle-fiber parallel to the MO5, a plain MO5 becomes the O4-plane, specifically the -plane, while an MO5 with an M5-brane on top of it becomes the -plane (Gimon 9, Sec. III8,Hanany-Kol 00, Sec. 3.1).
Hence the spacetime dimensions of the MO5 is the same that of the black M5-brane, but its charge as an O-plane is that of a single M5-brane (Dasgupta-Mukhil 95, Sec. 2, Witten 95, 3.3, Hori 98, 2.1), so that am M-theoretic lift of RR-field tadpole cancellation requires the presence of 16 M5-branes in a toroidal MO5-type orientifold .
As a sector of heterotic M-theory on ADE-singularities
By the classification of MFF 12, Sec. 8.3, the MO5-plane is not in fact a BPS solution of D=11 N=1 supergravity. But the intersection of an MK6 with an MO9-plane is a BPS solution to D=11 N=1 supergravity.
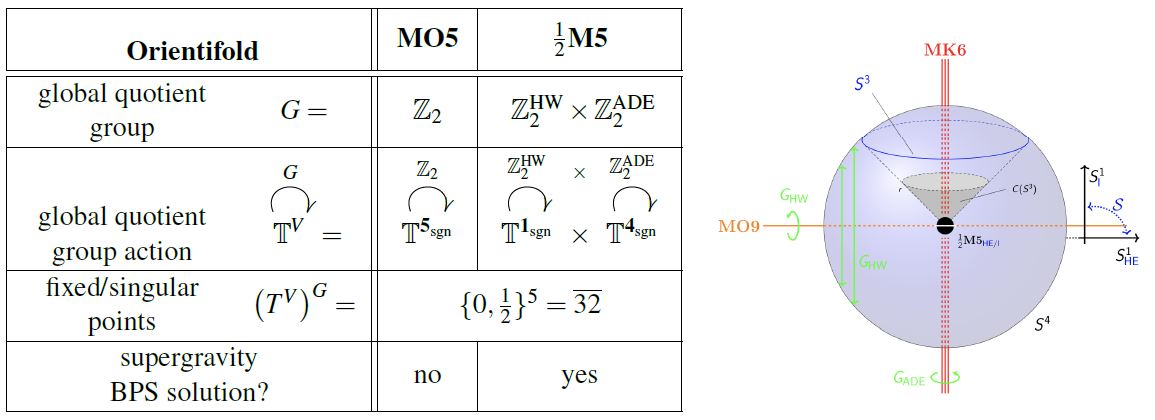
graphics grabbed from HSS18, Example 2.2.7
Thus, heterotic M-theory on ADE-orbifolds the MO5-plane becomes the fixed locus of the diagonal , hence the intersection of an MO9 with an MK6 (FLO 99, Sec. 4), also called the , since under duality between M-theory and type IIA string theory this becomes the half NS5-brane of type I' string theory.
As geometric engineering of SCFTs
Coincident M5-branes on an MO5-plane are supposed to geometrically engineer D=6 N=(2,0) SCFTs with D-series gauge groups (AKY 98, Sec. IIB).
But if these are really -branes of heterotic M-theory on ADE-orbifolds, then they will geometrically engineer D=6 N=(1,0) SCFTs, instead, see there.
References
General
The original articles are
-
Keshav Dasgupta, Sunil Mukhi, Orbifolds of M-theory, Nucl. Phys. B465 (1996) 399-412 (arXiv:hep-th/9512196)
-
Edward Witten: Five-branes And M-Theory On An Orbifold, Nucl. Phys. B 463 (1996) 383-397 [arXiv:hep-th/9512219, doi:10.1016/0550-3213(96)00032-6]
-
Kentaro Hori, Consistency Conditions for Fivebrane in M Theory on Orbifold, Nucl.Phys.B539:35-78, 1999 (arXiv:hep-th/9805141)
Classification view of rational equivariant Cohomotopy of super-spacetime:
- John Huerta, Hisham Sati, Urs Schreiber, Example 2.2.2 of: Real ADE-equivariant (co)homotopy and Super M-branes, CMP (2019) (arXiv:1805.05987, doi:10.1007/s00220-019-03442-3)
As a sector of the in heterotic M-theory at ADE-singularities
Discussion in the more general context of heterotic M-theory on ADE-orbifolds is in
- Michael Faux, Dieter Lüst, Burt Ovrut, Section 4 of Intersecting Orbifold Planes and Local Anomaly Cancellation in M-Theory, Nucl. Phys. B554: 437-483, 1999 (arXiv:hep-th/9903028)
and in view of super-embeddings of M5-branes in
-
Domenico Fiorenza, Hisham Sati, Urs Schreiber, Section 4 of: Super-exceptional geometry: origin of heterotic M-theory and super-exceptional embedding construction of M5 (arXiv:1908.00042)
-
Hisham Sati, Urs Schreiber: Equivariant Cohomotopy implies orientifold tadpole cancellation, Journal of Geometry and Physics 156 (2020) 103775 [doi:10.1016/j.geomphys.2020.103775, arXiv:1909.12277]
Relation to O4-planes
Relation of the MO5 to the O4-plane under duality between M-theory and type IIA string theory:
-
Kentaro Hori, Section 3 of: Consistency Conditions for Fivebrane in M Theory on Orbifold, Nucl. Phys. B539:35-78, 1999 (arXiv:hep-th/9805141)
-
Eric Gimon, On the M-theory Interpretation of Orientifold Planes (arXiv:hep-th/9806226, spire:472499)
-
Amihay Hanany, Barak Kol, Section 3.1 in: On Orientifolds, Discrete Torsion, Branes and M Theory, JHEP 0006 (2000) 013 (arXiv:hep-th/0003025)
-
Yoonseok Hwang, Joonho Kim, Seok Kim, M5-branes, orientifolds, and S-duality, J. High Energ. Phys. (2016) 2016: 148 (arXiv:1607.08557)
Geometric engineering of orthogonal , SCFTs
As geometric engineering of D=6 N=(2,0) SCFTs with D-series gauge groups:
- Changhyun Ahn, Hoil Kim, Hyun Seok Yang, SCFT and M Theory on , Phys.Rev. D59 (1999) 106002 (arXiv:hep-th/9808182)
Last revised on June 4, 2025 at 18:49:06. See the history of this page for a list of all contributions to it.