nLab super-embedding formalism

Idea

The “doubly supersymmetric geometric approach” (Bandos, Pasti, Sorokin, Tonin & Volkov 1995, Howe & Sezgin 1997), later named the super-embedding approach (Howe, Raetzel & Sezgin 1998, Sorokin 2000), is a formulation of super-$p$-brane sigma-models entirely within supergeometry, where not only the target spacetime is taken to be a supermanifold, as in Green-Schwarz sigma-models, and not only the worldvolume is taken to be a supermanifold, as in the NSR string, but where both are taken to be supermanifolds.

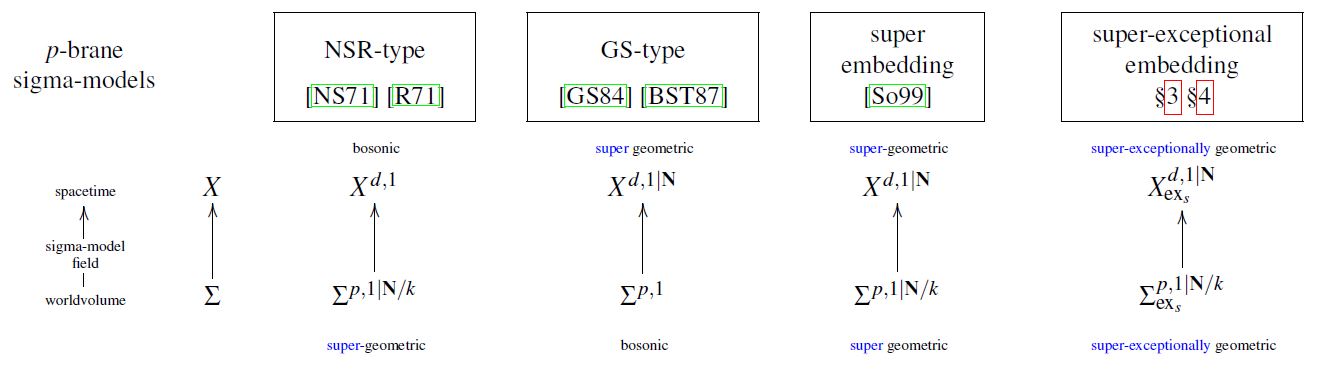
graphics grabbed from FSS 19c

The central observation of the super-embedding approach is that the equations of motion of super p-brane sigma-models are identified with nothing but a natural super-embedding condition on the super co-frame field on target superspacetime relative to the embedding $\phi \colon \Sigma \to X$ (really just: immersion) of the brane‘s worldvolume supermanifold:

1. on the bosonic components $E^a$ of the super co-frame field on target super-spacetime, the super-embedding condition is [Sorokin 2000 (4.36-37); Bandos 2011 (2.6-2.9); Bandos & Sorokin 2023 (5.13-14), strenghtening the original “geometrodynamical condition” of Bandos et al. 1995 (2.23)]:

   (1)$$\phi^\ast \, E^a \;\; = \;\; \left\{ \, \begin{array}{l} e^a & \text{for}\; a \leq p \\ 0 & \text{for}\, a \gt p \mathrlap{\,,} \end{array} \right.$$

   where $e^a$ are the bosonic components of the co-frame field on $\Sigma$, and where $1+p \coloneqq dim(\Sigma)$ is the dimension of its underlying bosonic manifold;

2. on the fermionic components $\Psi$ of the super co-frame field on target super spacetime the condition is [Sorokin 2000 (4.46); Bandos & Sorokin 2023 (5.26)]

   (2)$$\phi^\ast \, P \Psi \;\; = \;\; \psi \,,$$

   where $P \coloneqq \tfrac{1}{2}(1 + \Gamma_{p+1} \cdots \Gamma_d)$ is the corresponding transversal fermionic projector and $\psi$ are the fermionic components of the co-frame field on $\Sigma$.

Here we may observe [GSS24, §2] that a co-frame satisfying the bosonic “super-embedding condition” (1) is algebraically what is known in the mathematical literature as a (higher dimensional) Darboux coframe for the given immersion, see there.

Crucially, the would-be fermionic Darboux-condition $\phi^\ast \overline{P} \Psi = 0$ is not imposed (analogous to how the superspace-formulation of the target supergravity imposes the torsion constraint just on the bosonic coframe components): Remarkably, it turns out that the freedom in violating this would-be constraint accounts exactly for the presence of flux densities of higher gauge fields on the brane‘s worldvolume for the D-branes (with their Chan-Paton gauge field) and for the M5-brane (with its self-dual B-field in the D=6 N=(2,0) SCFT).

Properties

$\kappa$-Symmetry as super-general covariance

The notorious phenomenon of kappa-symmetry in Green-Schwarz sigma-models is revealed by the superembedding approach to be nothing but the odd-graded components of the super-diffeomorphism invariance on the worldvolume, hence: of super-general covariance (Sorokin-Tkach-Volkov 89, review includes Sorokin 00, section 4.3, Howe-Sezgin 04, section 4.3):

If

1. $X$ denotes a superspacetime locally modeled on super-Minkowski spacetime $\mathbb{R}^{d-1,1\vert \mathbf{N}}$

2. $\Sigma$ denotes a super-worldvolume of a super p-brane locally modeled on super-Minkowski spacetime $\mathbb{R}^{p,1\vert \mathbf{N}/2}$

3. so that a sigma-model field configuration for a super p-brane of shape $\Sigma$ to propagate in $X$ is a morphism of supermanifolds of the form

   $$\array{ \Sigma && \text{super-worldvolume} \\ \downarrow^{\mathrlap{\phi}} &&\text{sigma-model super-field}& \\ X && \text{super-spacetime} }$$

then:

1. the postcomposition action of spacetime super-isometries $X \stackrel{\simeq}{\longrightarrow} X$ is in even degree the action of spacetime isometries and in odd degree the action of spacetime supersymmetry on the sigma-model fields;

2. the precomposition action of worldvolume super-diffeomorphism $\Sigma \stackrel{\simeq}{\to} \Sigma$ is in even degree the action of bosonic worldvolume diffeomorphism and in odd degree the action of $\kappa$-symmetry:

$$\array{ \Sigma &\underoverset{\simeq}{\kappa\text{-symmetry}}{\longrightarrow}& \Sigma \\ \downarrow^{\mathrlap{\phi}} && \downarrow^{\mathrlap{\phi'}} \\ X &\underoverset{\simeq}{\text{spacetime supersymmetry}}{\longrightarrow}& X } \,.$$

Notice here the assumption that the number of odd directions on the worldvolume is half that of the target spacetime. This is the default assumption for fundamental super p-branes, and it directly reflects the statement that the corresponding black brane solutions are $1/2$ supergravity BPS states.

For example, consider the embedding

$$\mathbb{R}^{2,1} \hookrightarrow \mathbb{R}^{10,1}$$

of 2+1d Minkowski spacetime, thought of as the worldvolume of a membrane, into 11d Minkowski spacetime, linearly along the coordinate axis. Any such embedding breaks the isometry group of $\mathbb{R}^{10,1}$ from the 11d Poincaré group $Iso(10,1)$ to the product group

$$Iso(2,1) \times SO(8) \hookrightarrow Iso(10,1)$$

(meaning that this subgroup is the stabilizer subgroup of the embedding).

Now consider instead super Minkowski spacetime $\mathbb{R}^{10,1\vert \mathbf{32}}$ (with $\mathbf{32}$ the irreducible Majorana spinor representation in 11), hence the local model superspace for super spacetimes in 11-dimensional supergravity. We are to ask what subspace of the spin representation $\mathbf{32}$ preserves the embedding in that the spinor bilinear pairing $\overline{\psi}_1 \Gamma \psi_2$ on that subspace lands in $\mathbb{R}^{2,1} \hookrightarrow Iso(2,1) \hookrightarrow Iso(10,1)$ (Sorokin 2000, section 5.1). This is found to be the case for a half-dimensional subspace, and hence we may lift the above to a super-embedding of the form

(3)$$\mathbb{R}^{2,1\vert 8 \otimes \mathbf{2}} \hookrightarrow \mathbb{R}^{10,1\vert \mathbf{32}}$$

(where now $\mathbf{2}$ is the irreducible Majorana spinor representation in 3d, and $8 \otimes \mathbf{2}$ denotes the direct sum of 8 copies of it) such that the induced stabilizer supergroup inside the super Poincaré group now is

$$Iso(\mathbb{R}^{2,1\vert 8 \otimes \mathbf{2}}) \times Spin(8) \hookrightarrow Iso(\mathbb{R}^{10,1\vert \mathbf{32}}) \,.$$

It is in this sense that the membrane “breaks exactly half the supersymmetry”, namely from $\mathbf{32}$ to $8 \otimes \mathbf{2}$.

If one now thinks of this not as inclusions of global spacetimes, but of their super tangent spaces at the points where the membrane sits in spacetime, then this reflects the local structure of $\kappa$-symmetry: the $\kappa$-symmetries are locally generated by the 16 odd dimensions in $Iso(\mathbb{R}^{2,1\vert 8 \otimes \mathbf{2}} )$, being super-translations along the membrane worldvolume.

This explains why $\kappa$-symmetry in Green-Schwarz sigma models is taken to quotient out precisely half the spinor components, hence why, in the fully super-covariant formulation, one takes the worldvolume of a super $p$-brane in a superspacetime locally modeled on $\mathbb{R}^{d-1,1\vert \mathbf{N}}$ to be $\mathbb{R}^{p,1\vert \mathbf{N}/2}$. But notice that this is not a mathematical necessity. One may consider the worldvolume instead to have fewer odd directions. This then describes sigma models for “non-BPS super $p$-branes” (or rather “non-half-BPS” ).

Brane Lagrangians by relative trivialization

The super-embedding formalism has mostly been used for deriving equations of motion of super p-brane sigma-models.

But at least for some brane species, also their Lagrangian densities emerge naturally from the super-embedding, namely as relative trivializations of the brane cocycles as given by the brane scah/brane bouquet, relative to the superembedding:

BraneSuperEmbeddings.jpg

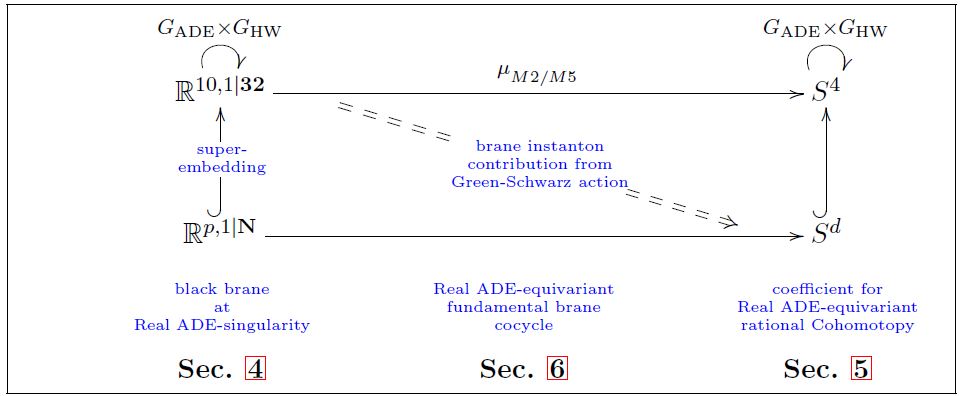
graphics grabbed from HSS 18

For strings and membranes

For the superstring and the super-membrane the construction of their Green-Schwarz sigma-model Lagrangian densities as relative trivialization of their super-cocycles along their super-embeddings is estalished in Howe-Sezgin 05 (4.72), HSS 18, Prop. 6.10:

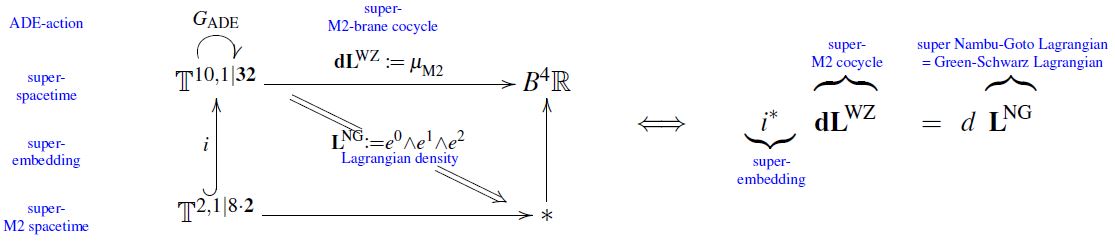
graphics grabbed from FSS 19c

For the M5-brane

In FSS 19c is offered a proof that combining super-embedding formalism with exceptional generalized geometry, the Perry-Schwarz-type Lagrangian for the M5-brane emerges as the relative trivialization of the super-cocycle of the M5-brane relative to its super-exceptional embedding.

Related concepts

manifest supersymmetry for brane sigma-models:

manifest worldvolume supersymmetry	manifest target+worldvolume supersymmetry	manifest target space supersymmetry
NSR action functional	superembedding approach	Green-Schwarz action functional

graphics grabbed from FSS19c

References

General

Early consideration of the idea of superstring sigma-models where both the worldsheet as well as the target spacetime are treated as supermanifolds is due (under the name “supersymmetry squared”) to:

• S. James Gates Jr., Hitoshi Nishino: $D = 2$ superfield supergravity, local $(supersymmetry)^2$ and non-linear 2 models, Classical and Quantum Gravity 3 3 (1986) 391-399 [doi:10.1088/0264-9381/3/3/013, spire:217518]

• R. Brooks, F. Muhammad, S. James Gates Jr.: Matter Coupled to $D=2$ Simple Unidexterous Supergravity, Local $(Supersymmetry)^2$ and Strings, Class. Quant. Grav. 3 5 (1986) 745-751 [doi:10.1088/0264-9381/3/5/005, spire:237390]

Under the name “doubly supersymmetric geometrical approach” discussion of the super-embedding condition originates in:

• Igor Bandos, Paolo Pasti, Dmitri Sorokin, Mario Tonin, Dmitry Volkov, Superstrings and supermembranes in the doubly supersymmetric geometrical approach, Nucl. Phys. B 446 (1995) 79-118 [arXiv:hep-th/9501113, doi:10.1016/0550-3213(95)00267-V]

• Paul S. Howe, Ergin Sezgin, Superbranes, Phys. Lett. B 390 (1997) 133-142 [arXiv:hep-th/9607227, doi:10.1016/S0370-2693(96)01416-5]

• Paul S. Howe, Ergin Sezgin, $D=11$, $p=5$, Phys. Lett. B 394 (1997) 62-66 [arXiv:hep-th/9611008, doi:10.1016/S0370-2693(96)01672-3]

The terminology “superembedding” arises with:

• Paul S. Howe, Ergin Sezgin, Peter C. West: Aspects of Superembeddings, in: Supersymmetry and Quantum Field Theory, Lecture Notes in Physics 509, Springer (1998) [doi:10.1007/BFb0105230, arXiv:hep-th/9705093]

• Paul S. Howe, O. Raetzel, Ergin Sezgin, On Brane Actions and Superembeddings, JHEP 9808 (1998) 011 [arXiv:hep-th/9804051, doi:10.1088/1126-6708/1998/08/011]

and a more elaborate discussion originates with:

• Dmitri Sorokin, Superbranes and Superembeddings, Phys. Rept. 329 (2000) 1-101 [arXiv:hep-th/9906142, doi:10.1016/S0370-1573(99)00104-0]

Generalization to intersecting branes is indicated in:

• C. S. Chu, Paul S. Howe, Ergin Sezgin, Peter C. West: Open superbranes, Physics Letters B 429 3–4 (1998) 273-280 [doi:10.1016/S0370-2693(98)00441-9]

Review:

• Igor Bandos, Paolo Pasti, Dmitri Sorokin, Mario Tonin, Superbrane actions and geometrical approach, in: Supersymmetry and Quantum Field Theory, Lecture Notes in Physics 509, Springer (1998) 79-91 [doi:10.1007/BFb0105231]

• Igor Bandos, Superembedding approach and generalized action in String/M-theory, in: Supersymemtries and Quantum Symmetries, Lecture Notes in Physics 524, Springer (1999) [arXiv:hep-th/9807202, doi:10.1007/BFb0104595]

• Dmitri Sorokin, Introduction to the Superembedding Description of Superbranes, AIP Conference Proceedings 589 98 (2001) [arXiv:hep-th/0105102, doi:10.1063/1.1419318]

• Igor A. Bandos, Superembedding approach to Dp-branes, M-branes and multiple D(0)-brane systems, Phys. Part. Nucl. Lett. 8 (2011) 149-172 [arXiv:0912.2530, doi:10.1134/S1547477111030046]

• Igor A. Bandos, Dmitri P. Sorokin, Superembedding approach to superstrings and super-$p$-branes, in: Handbook of Quantum Gravity, Springer (2023) [arXiv:2301.10668, doi:10.1007/978-981-19-3079-9_111-1]

Discussion in view of supersymmetry breaking:

• Paolo Pasti, Dmitri Sorokin, Mario Tonin, Superembeddings, Partial Supersymmetry Breaking and Superbranes, Nucl. Phys. B 591 (2000) 109-138 [arXiv:hep-th/0007048, doi:10.1016/S0550-3213(00)00569-1]

Related discussion in the bosonic situation:

• Igor Bandos, Wolfgang Kummer, P-Branes, Poisson-Sigma-Models and Embedding Approach to $(p+1)$-Dimensional Gravity, Int. J. Mod. Phys. A 14 (1999) 4881-4914 [arXiv:hep-th/9703099, doi:10.1142/S0217751X99002311]

Reformulation of “super-embeddings” via a supergeometric Darboux coframe-condition:

• Grigorios Giotopoulos, Hisham Sati, Urs Schreiber, §2 in: Flux Quantization on M5-Branes, Journal of High Energy Physics 2024 140 (2024) [arXiv:2406.11304, doi:10.1007/JHEP10(2024)140]

Actual examples of non-trivial super-embeddings (namely holographic super-embeddings of M5-branes and M2-branes):

• Grigorios Giotopoulos, Hisham Sati, Urs Schreiber: Holographic M-Brane Super-Embeddings, [arXiv:2408.09921]

$\kappa$-Symmetry

The super-geometric interpretation of kappa-symmetry as the odd-graded part of the action of super-diffeomorphism on the super p-brane worldvolume, regarded itself as a supermanifold was first suggested in

• Dmitri Sorokin, Vladimir Tkach, Dmitrij Volkov, Superparticles, twistors and Siegel symmetry, Mod. Phys. Lett. A 4 10 (1989) 901-908 [spire:271923, doi:10.1142/S0217732389001064]

Review of this perspective includes:

• Dmitri Sorokin, Superbranes and Superembeddings, Phys. Rept. 329 (2000) 1-101 [arXiv:hep-th/9906142, doi:10.1016/S0370-1573(99)00104-0]

• Paul Howe, Ergin Sezgin, section 4.3 of: The supermembrane revisited, Class. Quant. Grav. 22 (2005) 2167-2200 [arXiv:hep-th/0412245]

For the superstring

The equations of motion for the superstring have been derived via the superembedding approach in

• BPSTV 95, Chapter 4

See also

• Igor Bandos, Dmitrij Sorokin, Dmitrij Volkov, On the generalized action principle for superstrings and supermembranes, Phys. Lett. B 352 (1995) 269-275 [arXiv:hep-th/9502141]

For super AdS target spacetime:

• Igor A. Bandos: Superembedding approach to superstring in $AdS_5 \times S^5$ superspace, in: Fundamental Interactions (2009) 303-334 [arXiv:0812.0257, doi:10.1142/9789814277839_0018]

For the M2-brane

The equations of motion for the M2-brane have been derived via the superembedding approach in

• BPSTV 95, Chapter 3

and the Lagrangian density in

• Paul Howe, Ergin Sezgin, The supermembrane revisited, Class. Quant. Grav. 22 (2005) 2167-2200 (arXiv:hep-th/0412245)

For the M5-brane

The equations of motion for the M5-brane have been derived via the superembedding approach in

• Howe-Sezgin 97

following the superspace-computations in

• Paul Howe, Ergin Sezgin, Peter West, Covariant Field Equations of the M Theory Five-Brane, Phys. Lett. B 399 (1997) 49-59 [arXiv:hep-th/9702008, doi:10.1016/S0370-2693(97)00257-8]

reviewed in

• Sorokin 2000, Section 5.2

Discussion for 3+3-dimensional split:

• Sheng-Lan Ko, Dmitri Sorokin, Pichet Vanichchapongjaroen, The M5-brane action revisited, JHEP11(2013)072 (arXiv:1308.2231)

Claim that combining the super-embedding formalism with super-exceptional generalized geometry, the Perry-Schwarz-type Lagrangian for the M5-brane emerges as the relative trivialization of the super-cocycle of the M5-brane relative to its super-exceptional embedding:

• Domenico Fiorenza, Hisham Sati, Urs Schreiber: Super-exceptional geometry: Super-exceptional embedding construction of M5, J. High Energy Physics 2020 107 (2020) [doi:10.1007/JHEP02(2020)107, arXiv:1908.00042]

• Domenico Fiorenza, Hisham Sati, Urs Schreiber: Super-exceptional M5-brane model – Emergence of SU(2)-flavor sector, J. Geometry and Physics 170 (2021) 104349 [doi:10.1016/j.geomphys.2021.104349, arXiv:2006.00012]