nLab S5 modal logic
Context
-Category theory
Type theory
natural deduction metalanguage, practical foundations
type theory (dependent, intensional, observational type theory, homotopy type theory)
computational trinitarianism =
propositions as types +programs as proofs +relation type theory/category theory
Modalities
Contents
Idea
In modal logic the moniker “S5” refers to the logic obtained from S4 modal logic by adjoining the axiom scheme that there is the implication
In the possible worlds semantics for modal logic, S5 corresponds precisely to those Kripke frames where the relation is an equivalence relation [Kripke (1959) (1964), cf. Fagin, Halpern, Moses & Vardi (1995) Thm. 3.1.5 (c)].
Via dependent type theory
In mild generalization of the discussion at necessity & possibility – Via dependent types, we may observe that the modal operators in S5 Kripke semantics

(Here we are writing — following notation for subtypes — for a -dependent proposition, equivalently a proposition about the elements of , equivalently the subset of where the proposition holds.)
are precisely those arising as adjoint pairs of (co)monads induced on the left from a base change adjoint triple (the categorical semantics in Set of dependent pair type context extension dependent function type-formation) along display maps identified with the quotient coprojection of the Kripke frame:
(Obvious as this may be, the only existing reflection of this fact in the literature may be a side remark in Awodey 2006, p. 279, albeit not relating to dependent type formation.)
Remark
This suggests that one may equivalently regard dependent type theory as a universal form of epistemic modal type theory, in generalization of how modal logics may be viewed as just another perspective on (fragments of) first-order logic (as in Blackburn, van Benthem & Wolter (2007) pp. xiii): In both cases one switches perspective from type formation by base change adjoint triples (of quantification or dependent (co)product formation, respectively) to the induced adjoint pair of (co)monads. (Another example of a change in perspective of this form occurs when describing descent as monadic descent).
Remark
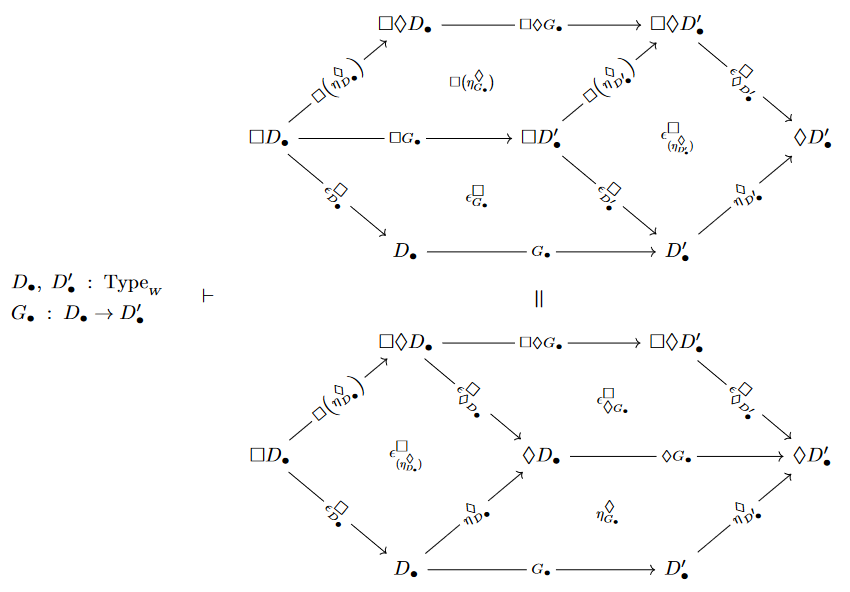
The above (co)monadic formulation of modal logic makes manifest another basic point not usually discussed in the subject, namely that the canonical epistemic entailments
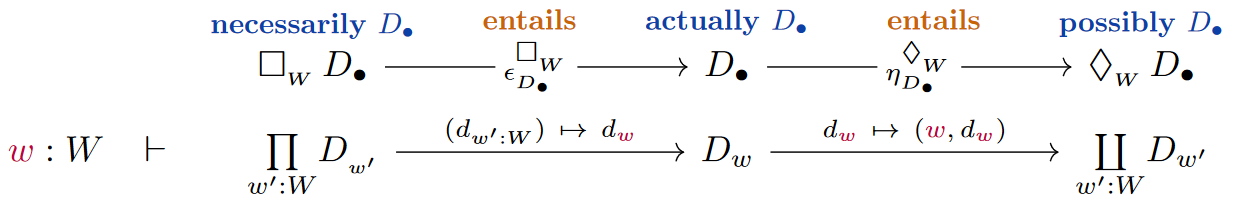
This means that the following squares commute. Their pasting to the hexagonal commuting diagram as shown may not have received attention (?):
Related concepts
| type of modal logic | relation in its Kripke frames |
|---|---|
| K modal logic | any relation |
| K4 modal logic? | transitive relation |
| T modal logic | reflexive relation |
| B modal logic? | symmetric relation |
| S4 modal logic | reflexive & transitive relation |
| S5 modal logic | equivalence relation |
(following BdRV (2001) Table 4.1; cf. Fagin, Halpern, Moses & Vardi (1995) Thm. 3.1.5)
References
General
The terminology “S5” in modal logic originates with:
- Clarence I. Lewis, Cooper H. Langford, App. II, p 501 of: Symbolic Logic (1932), Dover (2000) [App. II pdf]
The geometric model for S5 modal logic via Kripke frames originates with:
-
Saul A. Kripke, A Completeness Theorem in Modal Logic, The Journal of Symbolic Logic 24 1 (1959) 1-14 [doi:10.2307/2964568, jstor:2964568, pdf]
-
Saul A. Kripke, Semantical Analysis of Modal Logic I. Normal Modal Propositional Calculi, Mathematical Logic Quaterly 9 5-6 (1963) 67-96 [doi:10.1002/malq.19630090502]
See also:
- Wikipedia, S5 (modal logic)
A natural deduction-formulation and making explicit the modal operator as a comonad:
-
Gavin M. Bierman, Valeria de Paiva, Intuitionistic necessity revisited, School of Computer Science research reports-University of Birmingham CSR (1996) [researchgate, pdf]
-
Gavin M. Bierman, Valeria de Paiva, On an Intuitionistic Modal Logic Studia Logica 65 (2000) 383–416 [doi:10.1023/A:1005291931660, pdf]
-
Satoshi Kobayashi, Monad as modality, Theoretical Computer Science 175 1 (1997) 29-74 [doi:10.1016/S0304-3975(96)00169-7]
-
Natasha Alechina, Michael Mendler, Valeria de Paiva, Eike Ritter: Categorical and Kripke Semantics for Constructive S4 Modal Logic, in Computer Science Logic. CSL 2001 Lecture Notes in Computer Science 2142, Springer (2001) 292 [doi:10.1007/3-540-44802-0_21]
Understanding of S5 Kripke semantics as base change along the lines discussed at necessity and possibility – via dependent types:
- Steve Awodey, p. 279 in: Category theory, Oxford University Press (2006, 2010) [doi:10.1093/acprof:oso/9780198568612.001.0001, ISBN:9780199237180, pdf]
S5 modal logic as epistemic logic
Discussion of S5 modal logic as epistemic logic:
- Robert J. Aumann, Interactive epistemology I: Knowledge, International Journal of Game Theory 28 (1999) 263–300 doi:10.1007/s001820050111
Ditmarsch, Hoek & Kooi (2008): “in Aumann’s survey paper on interactive epistemology the reader will immediately recognise the system S5.”
-
Joseph Y. Halpern, Yoram Moses, §2.3 in: A guide to completeness and complexity for modal logics of knowledge and belief, Artificial Intelligence 54 3 (1992) 319-379 doi:10.1016/0004-3702(92)90049-4
-
Ronald Fagin, Joseph Y. Halpern, Yoram Moses, Moshe Y. Vardi, Reasoning About Knowledge, The MIT Press (1995) ISBN:9780262562003
p. 35: “in a precise sense the S5 properties completely characterize our definition of knowledge”
-
Joseph Y. Halpern, Should knowledge entail belief?, Journal of Philosophical Logic 25 5 (1996) 483-494 jstor:30226583, philpapers:HALSKE
-
Melvin Fitting, Logics of Knowlege, Sec. 9 in: Modal proof theory, Ch. 2 in: The Handbook of Modal Logic, Studies in Logic and Practical Reasoning 3 (2007) 85-183 doi:10.1016/S1570-2464(07)80005-X, book webpage
pp. 121: “What standard logics of knowledge capture is not actual knowledge, but potential knowledge — what one is entitled to know. The switch to potential knowledge means we drop all considerations of complexity It is easy to see that, under such an assumption, a knowledge modality should be a normal modal operator. But, what else should be required? All these together make a knowledge operator obey the S5 conditions.”
- Wiebe van der Hoek, Marc Pauly, Epistemic Logic, Sec 4 in: Modal logic for games and information, Ch. 20 in: The Handbook of Modal Logic, Studies in Logic and Practical Reasoning 3 (2007) 85-183 doi:10.1016/S1570-2464(07)80023-1, book webpage
p. 198: “Modal epistemic logic, the logic of knowledge, provides a very natural interpretation to the accessibility relation in Kripke models. For an agent , two worlds and are connected (written ), if the agent cannot (epistemically) distinguish them. In other words, we have if, according to ’s information at , the world might as well be in state , or that is compatible with i’s information at w. Using this interpretation of access, is obviously an equivalence relation. Thus, we are in the realm of the multi-modal logic .”
- Hans Ditmarsch, Wiebe Hoek, Barteld Kooi, Epistemic Logic, chapter 2 in: Dynamic Epistemic Logic, Studies In Epistemology, Logic, Methodology, And Philosophy Of Science (SYLI) 337, Springer (2008) doi:10.1007/978-1-4020-5839-4_2, pdf
p. 11: “The logical system S5 is by far the most popular and accepted epistemic logic”
-
Dov Samet, S5 knowledge without partitions, Synthese 172 (2010) 145–155 doi:10.1007/s11229-009-9469-0
-
Meghyn Bienvenu, Hélène Fargier, Pierre Marquis, Knowledge Compilation in the Modal Logic S5, Proceedings of the AAAI Conference on Artificial Intelligence 24 1 (2010) doi:10.1609/aaai.v24i1.7587, pdf
p. 1: “Propositional epistemic logic S5 is a well-known modal logic which is suitable for representing and reasoning about the knowledge of a single agent”
-
Rasmus Rendsvig, John Symons, Epistemic Logic, The Stanford Encyclopedia of Philosophy (2011) web
“Fagin, Halpern, Moses, and Vardi (1995) and many others use S5 for knowledge”
- Rachel Boddy, Epistemic Issues and Group Knowledge, Amsterdam (2014) pdf
p. 13: “Formal approaches to epistemology – such as game theory and computer science – typically assume the S5 conditions for knowledge, which is (partly) explained by the convenient formal properties of the logic. Philosophers typically opt for a weaker notion. Hintikka (1962), for instance, argues that the proper logic for knowledge is the modal system S4”
-
Yakoub Salhi and Michael Sioutis, A Resolution Method for Modal Logic S5, EPiC Series in Computer Science 36 (2015) 252–262 pdf
-
Ronald de Haan, Iris van de Pol, On the Computational Complexity of Model Checking for Dynamic Epistemic Logic with S5 Models arXiv:1805.09880
Last revised on August 3, 2023 at 19:08:23. See the history of this page for a list of all contributions to it.