nLab Topologie

this page is the German language version of (parts of) the page topology

---

Diese Seite behandelt Topologie als Untergebiet der Mathematik. Zu “Topologie” im Sinne von Struktur auf einer Menge, siehe topologischer Raum.

---

$\,$

$\,$

$\,$

Einführung

Im Folgenden geben wir eine kurze Einführung zu den zentralen Konzepten und Werkzeugen der Topologie.

• Stetigkeit

• Topologische Räume

• Homeomorphismen

• Homotopie

• Zusammenhangskomponenten

• Fundamentalgruppe

• Überlagerungsräume

Stetigkeit

Die zentrale Idee der Topologie ist es, Räume mit “stetigen Abbildungen” zwischen ihnen zu betrachten.

Historisch wurde das Konzept der Stetigkeit zuerst in der Analysis präzise gemacht, durch “epsilontische Analysis” von offenen Bällen, an diese wird unten in def. erinnert. Dann realisierte man dass dies eine elegantere Formulierung durch den Begriffe der offenen Mengen hat, dies ist unten Prop. . Der Begriff des topologischen Raumes ergibt sich wenn man von diesem allgemeinen Begriff der offenen Mengen ausgeht, dies ist Def. unten.

Sei daher zunächst an folgende elementare Begriffe der Analysis erinnert:

Definition

Ein metrischer Raum ist

1. eine Menge $X$ (die “zugrunde liegende Menge”);

2. eine Funktion $d \;\colon\; X \times X \to [0,\infty)$ (die “Distanzfunktion”) aus dem kartesischen Produkt der Menge mit sich selbst in die nicht-negativen reellen Zahlen

so dass für alle $x,y,z \in X$ gilt:

1. $d(x,y) = 0 \;\;\Leftrightarrow\;\; x = y$

2. (Symmetrie) $d(x,y) = d(y,x)$

3. (Dreiecksungleichung) $d(x,y)+ d(y,z) \geq d(x,z)$.

Beispiel

Jeder normierte Vektorraum $(V, {\Vert -\Vert})$ wird ein metrischer Raum im Sinne von Definition indem man setzt:

$$d(x,y) \coloneqq {\Vert x-y\Vert} \,.$$

Definition

Sei $(X,d)$, ein metrischer Raum. Dann heisst für jedes Element $x \in X$ und jede positive reelle Zahl $\epsilon \in \mathbb{R}_+$ die Menge

$$B^\circ_x(\epsilon) \;\coloneqq\; \left\{ y \in X \;\vert\; d(x,y) \lt \epsilon \right\}$$

der offene Ball von Radius $\epsilon$ um $x$.

Definition

(epsilontische Definition von Stetigkeit)

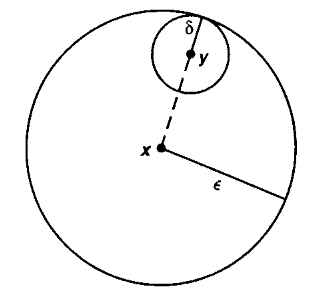
Seien $(X,d_X)$ und $(Y,d_Y)$ zwei metrische Räume (def. ), dann heisst eine Funktion

$$f \;\colon\; X \longrightarrow Y$$

stetig am Punkt $x \in X$ wenn für jedes $\epsilon \gt 0$ ein $\delta\gt 0$ existiert, so dass

$$d_X(x,y) \lt \delta \;\;\Rightarrow\;\; d_Y(f(x), f(y)) \lt \epsilon$$

oder äquivalent dazu, so dass

$$f(\;B_x^\circ(\delta)\;) \;\subset\; B^\circ_{f(x)}(\epsilon)$$

wobei $B^\circ$ den offenen Ball bezeichnet (Definition ).

Die Funktion $f$ heisst stetig wenn sie an jedem Punkt $x \in X$ stetig ist.

Wir formulieren diese analytische Begriffsbildung nun um, durch den einfachen aber wichtigen Begriff der offenen Menge:

Definition

(Umgebung und offene Menge)

Sei $(X,d)$ ein metrischer Raum (def. ). Dann sagt man

1. Eine Umgebung eines Punktes $x \in X$ ist eine Untermenge $x \in U \subset X$, welche mindestens einen offen Ball $B_x^\circ(\epsilon)$ um $x$ enthält (def. ).

2. Eine offene Menge von $X$ ist eine Untermenge $U \subset X$ die für jedes $x \in U$ auch noch eine Umgebung von $x$ enthält.

Das folgende Bild zeigt einen Punkt $x$, einige offene Bälle $B_i$ die $x$ enthalten, und zwei seiner Umgebungen $U_i$:

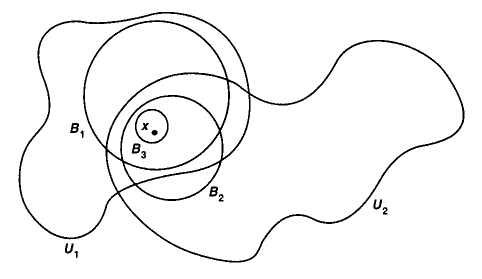
Illustration aus Munkres 75

Proposition

(Stetigkeit durch offene Mengen ausgedrückt)

Eine Funktion $f \colon X \to Y$ zwischen metrischen Räumen (def. ) ist stetig in dem epsilontischen Sinne von def. genau dann wenn sie die Eigenschaft hat dass:

• ihre Urbilder von offenen Mengen in $Y$ (im Sinne von def. ) sind auch offene Mengen von $X$.

Prinzip der Stetigkeit

$\,$ $\,$ Urbilder offener Mengen sind offen.

$\,$

Topologische Räume

Daher sollten wir uns also gut das Konzept von offenen Mengen ansehen. Es stellt sich heraus dass die folgende Abschlusseigenschaft das Konzept von offenen Mengen bereits sinnvoll charakterisiert.

Proposition

(Abschlusseigenschaft offener Mengen eines metrischen Raumes)

Die Menge aller offenen Mengen eines metrischen Raumes $(X,d)$ wie in def. hat die folgenden Eigenschaften:

1. Der Durchschnitt einer endlichen Zahl von offenen Mengen ist wieder eine offene Menge.

2. Die Vereinigung einer beliebigen Menge von offenen Mengen ist wieder eine offene Menge.

Insbesondere

• die leere Menge ist offen (als die Vereinigung keiner Untermenge)

und

• die ganze Menge $X$ selbst ist offen (als Durchschnitt keiner Untermenge).

Dies motiviert die folgende allgemeinere Definition:

Definition

(topologische Räume)

Gegeben eine Menge $X$, dann ist eine Topologie $\tau$ auf $X$ eine Menge von Untermengen von $X$ – die dann offene Mengen genannt werden – also eine Untermenge der Potenzmenge

$$\tau \subset P(X)$$

so dass diese unter folgenden Operatione abgeschlossen ist:

1. endliche Durchschnitte;

2. beliebige Vereinigungen.

Ein topologischer Raum ist eine Menge $X$ ausgestattet mit einer solchen Toplogie.

Die folgende Illustration zeigt alle Topologien auf der 3-Element Menge (bis auf Permutation der Elemente):

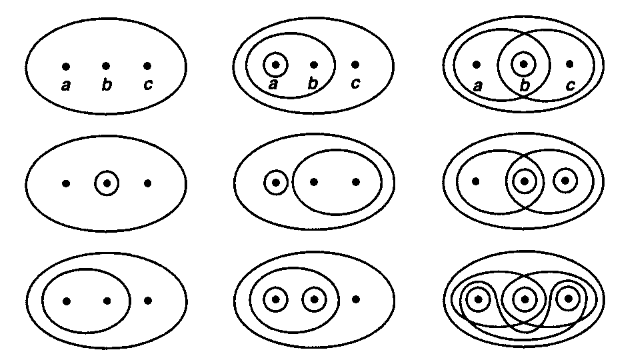
Illustration aus Munkres 75

Jetzt ist klar wie das Stetigkeitprinzip formalisiert wird.

Prinzip der Stetigkeit

$\,$ $\,$ Urbilder offener Mengen sind offen.

Definition

(stetige Abbildungen)

Eine stetige Abbildung zwischen topologsichen Räumen

$$f \colon (X, \tau_X) \to (Y, \tau_Y)$$

ist eine Funktion zwischen den unterliegenden Mengen,

$$f \colon X \longrightarrow Y$$

so dass Urbilder unter $f$ von offenen Mengen in $Y$ wieder offene Mengen in $X$ sind.

Diese einfach Definition von offenen Untermengen und das einfache Stetigkeitprinzip geben der Topologie ihr fundamentales und universelles Gepräge. Die kombinatoischen Natur dieser Definition macht dass Topologie enge Bezüge zur formalen Logik hat (mehr dazu siehe locale).

Bemerkung

(die Kategorie der topologischen Räume)

Die Komposition von stetigen Abbildungen ist offensichtlich assoziativ und unital.

Man sagt dass

1. topologische Räume sind die Objekte

2. stetige Abbildungen sind die Morphismen (Homomorphismen)

einer Kategorie. Die Kategorie der topologischen Räume (kurz: Top ).

Es ist nützliche eine Ansammlung von Objekten mit Morphismen dazwischen durch Diagramme darzustellen, wie dieses:

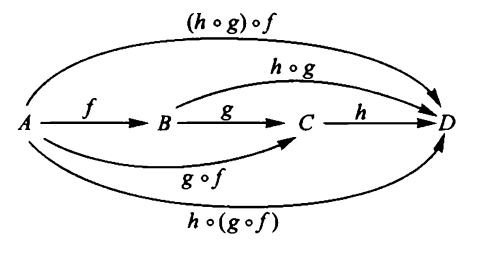
Illustration aus Lawvere-Schanuel 09.

Unser motivierendes Beispiel ist also folgendes

Beispiel

(metrische Topologie)

Sei $(X,d)$ ein metrischer Raum. Dann ist seine Menge von offenen Mengen im Sinne von def. eine Topologie auf $X$, macht also $X$ zu einem topologischen Raum im Sinne von def. . Dies wird die metrische topologie genannt.

Kurz gesagt, die offenen Bälle in einem metrischen Raum sind die “Basis” für die metrische Topologie.

Ein wichtiger Punkt der allgemeinen Definition von “topologischem Raum” ist dass sie Konstruktionen zulässt die intuitiv auf “stetigen Räumen” existieren sollten, aber dies sonst, zum Beispiel in metrischen Räumen, nicht tun:

Beispiel

(diskrete topologische Räume)

Sei $S$ eine Menge, dann betrachtet die diskrete Topologie auf $S$ jede Untermenge von $S$ als offene Untermenge.

Beispiel

(Unterraum Topologie)

Sei $(X, \tau_X)$ ein topologischer Raum, und sei $X_0 \hookrightarrow X$ eine Untermenge der zugrunde liegenden Menge. Die zugehörige Unterraumtopologie hat dann

• $X_0$ als ihre zugunde liegende Menge,

• die offenen Untermengen sind die Untermengen von $X_0$, welche Einschränkungen von offenen Untermengen in $X$ sind.

(Dies wird auch die initiale Topologie der Injektionsabbildung genannt.)

Die Illustration rechts zeigt zwei offene Untermengen in dem Quadrat, betrachtet als topologischer Unterraum der Ebene $\mathbb{R}^2$:

Illustration aus Munkres 75

Beispiel

(topologischer Quotientenraum)

Sei $(X,\tau_X)$ ein topologischer Raum (def. ) und sei

$$R_\sim \subset X \times X$$

eine Äquivalenzrelation auf der zugrunde liegenden Menge. Dann hat der topologische Quotientenraum

• als zugrunde liegende Menge die quotientenmenge $X_{\sim}$, also die Menge von Äquivalenzklassen,

und

• eine Untermenge $O \subset X_{\sim}$ wird als offene Untermenge betrachtet genau dann wenn ihr Urbild $\pi^{-1}(O)$ under der kanonischen Projektionsabbildung

  $$\pi \colon X \to X_\sim$$

  eine offene Untermenge von $X$ ist.

(Dies wird auch die finale Topologie der Projektion $\pi$ genannt.)

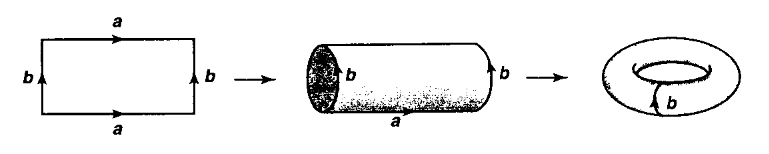
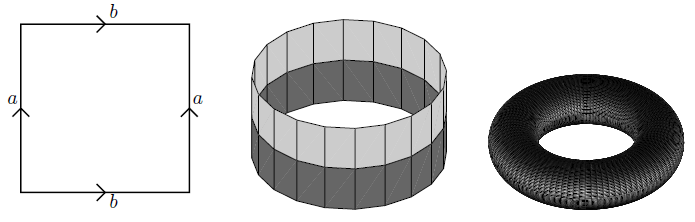
Die obige Illustration zeigt links das Quadrat (ein topologischer Unterraum der Ebene), dann in der Mitte den resultierenden topologischen Quotientenraum erhalten durch Identifizierung zweier gegenüberliegender eiten (der Zylinder), und rechts den weiteren Quotientenraum erhalten durch identifizierung auch der verbleibenden beiden Seiten (der Torus).

Illustration aus Munkres 75

Beispiel

(topologischer Produktraum)

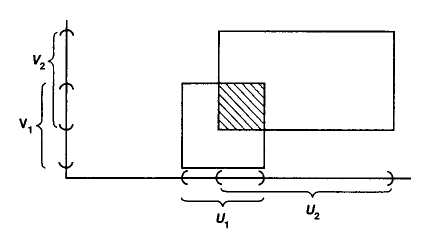
Seien $X$ und $Y$ zwei topologische Räume, dann hat der topologische Produktraum $X \times Y$

• als zugrunde liegende Menge das kartesische Produkt der unterliegenden Mengen $X$ and $Y$,

und

• seine offenen Mengen sind die Untermengen $O \subset X \times Y$ des kartesischen Produktes für die gilt dass für alle Punkte $(x,y) \in O$ offene Mengen $x \in O_x \subset X$ und $y \in O_Y \subset Y$ existieren, so dass $O_x \times O_y \subset O$.

Illustration aus Munkres 75

Diese Konstruktionen vondisketen topologischen Räumen, topologischen Quotientenräumen, topologischen Unterräumen und von topologischen Produkträumen snd einfache Beispiele für Limiten und Kolimiten von topologischen Räumen. Die Kategorie Top von topologischen Räumen hat die nützliche Eigenschaft dass alle Limiten und Kolimiten (über kleine Diagramme) in ihr existieren (mehr dazu siehe Top – Universelle Konstruktionen.)

Homeomorphismen

Mit den Objekten (topologischen Räumen) und den Morphismen (stetige Abbildungen) der Kategorie Top der Topologie also definiert, erhalten wir den Begriff der “Gleichheit” in der Topologie.

Um dies präzise zu machen sagt man dass ein Morphismus

$$X \overset{f}{\to} Y$$

in einer Kategorie ein Isomorphismus ist wenn ein weiterer Morphismus in die andere Richtung existiert

$$X \overset{f^{-1}}{\longleftarrow} Y \,,$$

welcher invers zu $f$ ist in dem Sinne dass

$$f \circ f^{-1} = id_Y \;\;\;\;\; and \;\;\;\;\; f^{-1} \circ f = id_X \,.$$

Definition

(Homeomorphismen)

Ein Isomorphismus in der Kategorie Top von topologischen Räumen mit stetigen Abbildungen zwischen ihnen heisst Homeomorphismus.

Das ist also eine stetige Abbildung

$$f \;\colon\; X \longrightarrow Y$$

so dass ein dazu inverser Morphismus existiert, nämich eine stetige Funktion in der anderen Richtung

$$X \longleftarrow Y \;\colon\; f^{-1}$$

so dass

$$f \circ f^{-1} = id_{Y} \;\;\;and\;\;\; f^{-1} \circ f = id_{X} \,.$$

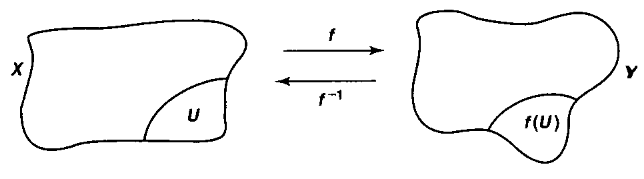
Illustration aus Munkres 75

Beispiel

(offenes Intervall homöomorph zur reellen Geraden)

Das offene Intervall $(-1,1)$ ist homöomorph zu der gesamten reellen Geraden

$$(0,1) \underset{homeo}{\simeq} \mathbb{R}^1 \,.$$

Ein inverses Paar von stetigen Funktionen ist zum Beispiel gegeben durch

$$\array{ f &\colon& \mathbb{R}^1 &\longrightarrow& (-1,+1) \\ && x &\mapsto& \frac{x}{\sqrt{1+ x^2}} }$$

and

$$\array{ f^{-1} &\colon& (-1,+1) &\longrightarrow& \mathbb{R}^1 \\ && x &\mapsto& \frac{x}{\sqrt{1 - x^2}} } \,.$$

Allgemein ist jeder offene Ball in $\mathbb{R}^n$ (def. ) homöomorph zum ganzen $\mathbb{R}^n$.

Beispiel

(Intervall an den Endpunkten verklebt ist homöomorph zum Kreis)

Als topologische Räume ist das Intervall mit identifizierten Endpunkten homöomorph (def. ) zum Einheitskreis:

$$[0,1]_{/(0 \sim 1)} \;\; \underset{homeo}{\simeq} \;\; S^1 \,.$$

Mehr im Detail: Sei

$$S^1 \hookrightarrow \mathbb{R}^2$$

der Einheitskreis in der Ebene

$$S^1 = \{(x,y) \in \mathbb{R}^2, x^2 + y^2 = 1\}$$

ausgestattet mit der Unterraumtopologie (Beispiel ) der Ebene $\mathbb{R}^2$, welche selbst mit ihrer standard metrischen Topologie (Beispiel ) ausgestattet ist.

Darüberhinaus, sei

$$[0,1]_{/(0 \sim 1)}$$

der topologische Quotientenraum (Beispiel ) der aus dem Intervall $[0,1] \subset \mathbb{R}^1$ mit seine Unterraumtopologie erhalten wird durch Anwendung der Äquivalenzrelation, welche die beiden Endpunkte identifiziert (und sonst nichts).

Betrachte dann die Funktion

$$f \;\colon\; [0,1] \longrightarrow S^1$$

gegeben durch

$$t \mapsto (cos(t), sin(t)) \,.$$

Diese hat die Eigenschaft dass $f(0) = f(1)$, so dass die also absteigt zu einer Funktion auf dem topologischen Quotientenraum

$$\array{ [0,1] &\overset{}{\longrightarrow}& [0,1]_{/(0 \sim 1)} \\ & {}_{\mathllap{f}}\searrow & \downarrow^{\mathrlap{\tilde f}} \\ && S^1 } \,.$$

Wir behaupten dann $\tilde f$ ein Homöomorphismus ist (Definition ).

Zunächst ist es klar dass $\tilde f$ eine stetige Funktion ist. Das folgt direkt aus der tatsache dass $f$ eine stetige Funktion ist und per Definition der Quotiententopologie (Beispiel ).

Wir müssen also prüfen dass $\tilde f$ eine stetige inverse Funtion hat. Offensichtlich hat die Einschränkung von $f$ selbst auf das offene Intervall $(0,1)$ ein stetiges Inverses. Es hat kein stetiges Inverses auf $[0,1)$ und auf $(0,1]$ und hat überhaupt kein Inverses auf [0,1], weil $f(0) = f(1)$. Aber die Relation $[0,1]_{/(0 \sim 1)}$ hat genau die Eigenschaft dass sie diese Probleme herausteilt.

Analog gilt:

Das Quadrat $[0,1]^2$ mit zwei seiner Seiten identifiziert ist der Zylinder, und mit zwei weiteren Seiten identifiziert der Torus:

Wenn die Seiten hingegen mit umgekehrter Orientierung identifiziert werden, dann ist das Resultat das Möbiusband:

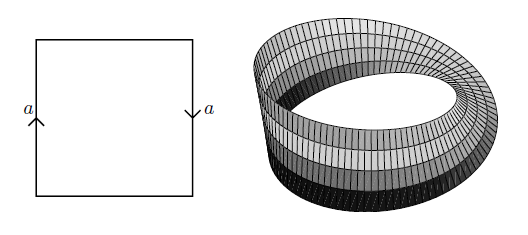
Illustration aus Lawson 03

$\,$

Wichtige Beispiele von topologischen Räumen die nicht homöomorph sind, enthalten die folgenden:

Theorem

(topologische Invarianz der Dimension)

Seien $n_1, n_2 \in \mathbb{N}$ aber $n_1 \neq n_2$, dann sind die kartesischen Räume $\mathbb{R}^{n_1}$ und $\mathbb{R}^{n_2}$ nicht homöomorph.

Allgemeiner, eine offene Menge in $\mathbb{R}^{n_1}$ ist nie homöomorph zu einer offenen Menge in $\mathbb{R}^{n_2}$ wenn $n_1 \neq n_2$.

Der beweis des Theorems ist überraschend anspruchsvoll, angesichts wie offensichtlich die Aussage intuitiv erscheint. Man benötigt Werkzeuge der algebraischen Topologie (insbesondere den Fixpunktsatz von Brouwer).

Wir illustrieren nun die Werkzeuge der algebraischen Topologie und demonstrieren die Natur ihrer Anwednung durch den Beweis zweier sehr einfacher Spezialfälle der topologischen Invarianz der Dimension (prop. und prop. unten).

Beispiel

(Homeomorphismusklassen von Flächen)

Die 2-sphere $S^2 = \{(x,y,z) \in \mathbb{R}^3 \vert x^2 + y^2 + z^2 = 1\}$ ist nicht homöomorph zu dem Torus $T^2 = S^1 \times S^1$.

Allgemein ist die Homeomorphismusklasse einer geschlossenen orientierbaren Fläche durch die Anzahl der “Löcher” determiniert die die Fläche hat: ihr Geschlecht.

$\,$

Homotopie

Wir haben oben gesehen dass für $n \geq 1$ der offene Ball $B_0^\circ(1)$ in $\mathbb{R}^n$ nicht homöomorph zu, insbesondere, dem Punkt $\ast = \mathbb{R}^0$ ist (Beispiel , Theorem ). Dennoch ist intuitiv der $n$-Ball eine “stetige Deformierung” des Punktes, den man erhält wenn der Radius des $n$-Balles nach null geht.

Diese Intuition wird durch die Beobachtung präzisiert dass ein stetige Funktion existiert auf dem topologischen Produktraum (Beispiel ) des offenen Balles mit dem geschlossenen Intervall

$$\eta \colon [0,1] \times B_0^\circ(1) \longrightarrow \mathbb{R}^n$$

gegeben durch Reskalierung:

$$(t,x) \mapsto t \cdot x \,.$$

Dies interpoliert stetig zwischen dem offenen Ball und dem Punkt, in dem Sinne dass für $t = 1$ die Abbildung sich auf die definierende Einbettung einschränkt $B_0^\circ(1)$, währende sie für $t = 0$ konstant ist.

Wir können diese Siutation zusammenfassen durch ein Diagramm von stetigen Abbildungen der folgenden Form:

$$\array{ B_0^\circ(1) \times \{0\} \\ \downarrow & \searrow^{\mathrlap{x \mapsto 0}} \\ [0,1] \times B_0^\circ(1) &\overset{(t,x) \mapsto t \cdot x}{\longrightarrow}& \mathbb{R}^n \\ \uparrow & \nearrow_{\mathrlap{inclusion}} \\ B_0^\circ(1) \times \{1\} }$$

Solche “stetigen Deformationen” heissen Homotopien:

Definition

(Homotopie)

Seien $f,g\colon X \longrightarrow Y$ zwei stetige Funktionen zwischen topologischen Räumen $X,Y$, dann ist eine (linke) Homotopie

$$\eta \colon f \,\Rightarrow_L\, g$$

eine stetige Funktion

$$\eta \;\colon\; X \times I \longrightarrow Y$$

aus dem topologischen Produktraum (Beispiel ) des offenen Balles mit dem standard Intervall, so dass dies in ein kommutierendes Diagramm der folgenden Form passt:

$$\array{ {0} \times X \\ {}^{\mathllap{(id,\delta_0)}}\downarrow & \searrow^{\mathrlap{f}} \\ [0,1] \times X &\stackrel{\eta}{\longrightarrow}& Y \\ {}^{\mathllap{(id,\delta_1)}}\uparrow & \nearrow_{\mathrlap{g}} \\ \{1\} \times X } \,.$$

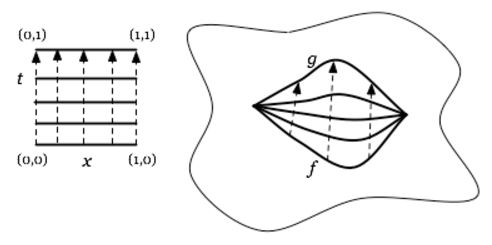
Illustration von J. Tauber here

Definition

(Homotopieäquivalenz)

Eine stetige Funktion $f \;\colon\; X \longrightarrow Y$ heisst Homotopieäquivalenz wenn

1. es eine stetige Abbildung in der anderen Richtung gibt, $g \;\colon\; Y \longrightarrow X$,

2. sowie left homotopies, def. , from the two composites to the identity:

$$\eta_1 \;\colon\; f\circ g \Rightarrow_L id_Y$$

and

$$\eta_2 \;\colon\; g\circ f \Rightarrow_L id_X \,.$$

Beispiel

(der offene Ball ist kontrahierbar)

Jeder offene Ball (oder geschlossene Ball) also (nach Beispiel ) auch jeder kartesische Raum ist homotopieäquivalent zum Punkt

$$\mathbb{R}^n \underset{homotopy}{\simeq} \ast \,.$$

Beispiel

Die folgenden drei Graphen

(also die offensichtlichen topologischen Unterräume der Ebene $\mathbb{R}^2$ die diese Bilder anzeigen) sind nicht homöomorph. Aber sie sind homotopieäquivalent, tatsächlich sind sie alle homotopieäquivalent zur Scheibe aus der zwei Punkte entnommen sind, kraft der Homotopien die in folgenden Bildern angedeutet sind:

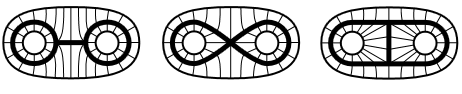
Illustration aus Hatcher

$\,$

Zusammenhangskomponenten

Unter Verwendung des Begriffs der Homotopie erhält man die grundlegnden Werkzeuge der algebraischen Topologie, nämlich die Konstruktion algebraischer Homotopieinvarianten von topologischen Räumen. Wir führen hier die einfachsten dieser Werkzuge ein und illustrieren deren Anwendung.

Bespiel

Eine Homotopie zwischen zwei Punkten

$x,y \;\colon\; \ast \to X$

ist einfach ein stetiger Pfad zwischen diesen Punkten.

Definition

(Zusammenhangskomponenten)

Die Megen der Homotopieklassen von Punkten in einem topologischen Raum $X$ heisst die Menge der Pfadzusammenhangskomponenten, bezeichnet durch

$$\pi_0(X) \in Set \,.$$

Wen $\pi_0(X) \simeq \ast$ ein einzelnes Element enthält, dann heisst $X$ ein pfad-zusammenhängender topologischer Raum.

Wenn $f \colon X \to Y$ eine stetige Abbildung zwischen topologischen Räumen ist, dann indizuiert sie auf Homotopieklassen von Punkten eine Funktion zwischen den Zusammenhangskomponenten. Diese bezeichnen wir durch:

$$\pi_0(f) \;\colon\; \pi_0(X) \longrightarrow \pi_0(Y) \,.$$

Diese Konstruktion ist offenbar mit Komposition verträglich, in dem Sinne dass

$$\pi_0(g \circ f) = \pi_0(g) \circ \pi_0(f)$$

und ist offensichtlich unital, in dem Sinne dass

$$\pi_0(id_X) = id_{\pi_{0}(X)} \,.$$

Man fasst diesen sachverhalt zusammen indem man sagt dass $\pi_0$ Funktor ist von der Kategorie Top von topologischen Räumen zu der Kategorie Set der Mengen:

$$\pi_0 \;\colon\; Top \longrightarrow Set \,.$$

Eine offensichtliche aber wichtige Konsequen ist dies:

Proposition

Wenn die Mengen von Zusammenhangskomponenten zweier topologischer Räume nicht bijektiv sind, dann können die beiden Räume nicht homöomorph zueinander sein:

$$\pi_0(X) \neq \pi_0(Y) \;\;\; \Rightarrow \;\;\, X \underset{homeo}{\neq} Y$$

Beweis

Da $\pi_0$ funktoriell ist, folgt sofort das es Isomorphismen auf Isomorphismen schickt, also Homöomorphismen auf Bijektionen:

$$\begin{aligned} & f \circ g = id \;\;and\;\; g \circ f = id \\ \Rightarrow \;\;\;\;\;\;& \pi_0(f \circ g) = \pi_0(id) \;\;und \;\; \pi_0(g \circ f) = \pi_0(id) \\ \Leftrightarrow \;\;\;\;\;\; & \pi_0(f) \circ \pi_0(g) = id \;\;und \;\; \pi_0(g) \circ \pi_0(f) = id \end{aligned} \,.$$

Dies bedeutet dass wir dir Zuammenhangskomponenten als eine erste “topologische Invariante” betrachten können, welche uns erlaubt manche topologischen Räume zu unterscheiden.

Prinzip der algebraischen Topologie

$\,\,$ Verwende topologische Invarianten um topologische Räume zu unterscheiden.

Als Anwendungsbeispiel haben wir den folgenden Beweis eines Spezialfalls der topologischen Invarianz der Dimension (Theorem ):

Proposition

(topologische Invarianz der Dimension – erster einfacher Fall)

Die kartesische Räume $\mathbb{R}^1$ und $\mathbb{R}^2$ sind nicht homöomorph (def. ).

Beweis

Wir nehmenn an e gäbe einen Homöomorphismus

$$f \colon \mathbb{R}^1 \longrightarrow \mathbb{R}^2$$

und werden einen Widerspruch erhalte. Sei also $f$ ein Homeomorphismus, dann ist offensichtlich auch seine Einschränkung auf den topologischen Unterraum (Beispiel ) den man durch Entfernen des Ursprunges $0 \in \mathbb{R}^1$ and $f(0) \in \mathbb{R}^2$ erhält ein Homeomorphismus:

$$f \;\colon\; (\mathbb{R}^1-\{0\}) \longrightarrow (\mathbb{R}^2 - \{f(0)\}) \,.$$

Es folgt also dass wir ein Bijektion zwischen den Zusammenhangskomponenten $\pi_0(\mathbb{R}^1 - \{0\})$ und $\pi_0(\mathbb{R}^2 - \{f(0)\})$ erhalten würden. Aber eine solche existiert offensichtlich nicht, da letztere Menge nur ein Element enthält, aber erstere Menge zwei Elemente enhält (die negativen und die positiven Zahlen )

$$\pi_0(\mathbb{R}^1-\{0\}) \;\neq\; \pi_0(\mathbb{R}^2 - \{f(0)\}) \,.$$

Die Lehre aus dem beweis von prop. ist seine Strategie:

Prinzip der algebraischen Topologie

$\,\,$ Verwende topologische Invarianten um topologische Räume zu unterscheiden.

Natürlich verwendet man in der Praxis stärkere Invarianten als nur $\pi_0$.

Die enächset topologische Invariante nach den Zusammenhangskomponenten ist die Fundamentalgruppe:

Fundamentalgruppe

Definition

(Fundamentalgruppe)

Sei $X$ ein topologischer Raum und sein $x \in X$ ein gegebener Punkt. Dann schreiben wir

$$\pi_1(X,x) \;\in\; Grp$$

für, zunächst, die Menge von Homotopieklassen von Pfaden in $X$ die bei $x$ starten und enden. Solche Pfade heissen stetige Schleifen in $X$ basiert bei $x$.

1. Unter Aneinanderhängen von Schleifen wird $\pi_1(X,x)$ zu einer Semigruppe;

2. die konstante Schleife ist neutrales Element und macht $\pi_1(X,x)$ zu einem “Monoiden”.

3. Umkehrung von Schleifen schickt sie auf ihr Inverses, und macht $\pi_1(X,x)$ zu einer Gruppe.

Diese heisst die Fundamentalgrupp $\pi_1(X,x)$ von $X$ bei $x$.

Das folgende Bild deutet die vier nicht-trivialen Generatoren der Fundamentalgruppe der orientierten Fläche vom Geschlecht 2:

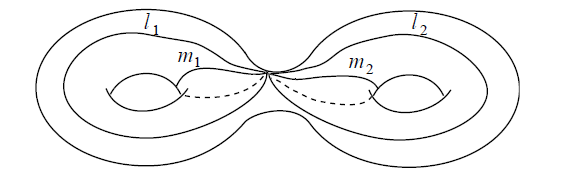
Illustration aus Lawson 03

Auch diese Konstruktion ist funktoriell, nun auf der category $Top^{\ast/}$ von punktierten topologischen Räumen:

$$\pi_1 \;\colon\; Top^{\ast/} \longrightarrow Grp \,.$$

As $\pi_0$, so also $\pi_1$ is a topological invariant. As before, we may use this to prove a simple case of the theorem of the topological invariance of dimension:

Definition

Ein topologischer Raum $X$ für den

1. $\pi_0(X) \simeq \ast$ (pfad-zusammenhängend, def. )

2. $\pi_1(X,x) \simeq 1$ (die Fundamentalgruppe ist trivial, def. ),

heisst einfach zusammenhängend.

Proposition

(topologische Invarianz der Dimension – zweites einfaches Beispiel)

Es gibt keinen Homöomorphismus zwischen $\mathbb{R}^2$ und $\mathbb{R}^3$.

Beweis

Wir nehmen an es gäbe einen Homeomorphismus $f$ und werden einen Widerspruch herleiten.

Sei also $f$ ein Homeomorphismus, dann ist auch seine Einschränkung auf das Komplement eines Punktes einer

$$(\mathbb{R}^2 - \{0\}) \longrightarrow (\mathbb{R}^3 - \{f(0)\}) \,.$$

Diese Räume sind beide zusammenhängend, lassen sich also durch $\pi_0$ nicht unterscheiden.

Aber ihre Fundamentalgruppen $\pi_1$ sind unterschiedlich:

1. Die Fundamentalgruppe von $\mathbb{R}^{2} - \{0\}$ ist $\mathbb{Z}$ (die Windungszahl von Schleifen um den entfernten Punkt). Wir diskutieren dies näher unten in Beispiel .

2. Die Fundamentalgruppe von $\mathbb{R}^3 - \{f(0)\}$ its trivial: der einzelne fehlende Punkt hindert nicht daran Schleifen beliebig zusammenzuziehen.

Aber weil die Konstrution der Fundamentalgruppefunktiell sit, so folgt, mit de gleichen Argument wie in dem Beweis von Prop. , dass also $f$ kein Isomorphismus sein kein, also kein Homöomorphismus.

$\,$

Überlagerungsraum

Wir diskutieren nun eine “duale Erscheinungsform” der Fundamentalgruppe $\pi_1$, welche oft hilft sie zu berechnen.

Definition

(Überlagerungsraum)

Ein Überlagerungsraum über einem topologischer Raum $X$ ist eine stetige Abbildung

$$p \;\colon\; E \longrightarrow X$$

so dass eine offene Überdeckung existiert

$$\underset{i}{\sqcup}U_i \longrightarrow X$$

so dass die Einschränkung von $E \overset{p}{\to} X$ auf jedes der homöomorph ist zu dem topologischen Produktraum (Beispiel ) von $U_i$ mit dem diskreten topologischen Raum (Beispiel ) auf einer Menge $F_i$:

$$\array{ \underset{i}{\sqcup} U_i \times F_i &\longrightarrow& E \\ \downarrow &(pb)& \downarrow^{\mathrlap{p}} \\ \underset{i}{\sqcup} U_i &\underset{}{\longrightarrow}& X } \,.$$

Für $x \in U_i \subset X$ ein Punkt heissen die Element von $F_x = F_i$ die Blätter der Überlagerung an diesem Punkt.

Beispiel

(Überdeckung des Kreises durch den Kreis)

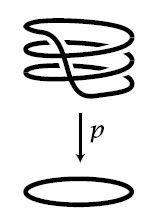
Betrachte den Kreis $S^1 = \{ z \in \mathbb{C} \;\vert\; {\vert z\vert} = 1 \}$ als den topologischen Unterraum von Elementen mit Betrag 1 in der komplexen Ebene. Für $k \in \mathbb{N}$, betrachte die stetige Funktion

$$p \coloneqq (-)^k \;\colon\; S^1 \longrightarrow S^1$$

die eine komplexe Zahl auf ihr $k$-te Potenz schickt.

Man denk sich dies als “der Kreis windet sich $k$ mal um sich selbst”. Präzise: für $k \geq 1$ ist dies ein Überlagerungsraum (Def. ) mit $k$ Blättern an jedem Punkt.

Illustration aus Hatcher

Beispiel

(Überlagerung des Kreises durch die reelle Gerade)

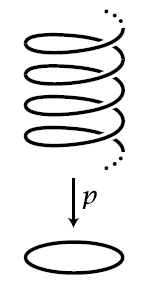
Betrachte die stetige Funktion

$$\exp(2 \pi i(-)) \;\colon\; \mathbb{R}^1 \longrightarrow S^1$$

von der reellen Geraden zum Kreis, welche

1. mit the Kreis betrachtet als der Einheitskreis in der komplexen Ebene $\mathbb{C}$ durch

   $$t \mapsto \exp(2\pi i t)$$

   gegeben ist

2. mit dem Kreis betrachtet als Einheitskreis in $\mathbb{R}^2$ durch

   $$t \mapsto ( cos(2\pi t), sin(2\pi t) )$$

   gegeben ist.

Man darf sich dies vorstellen als “das unendliche Umwickeln des Kreises durch die reelle Achse”.

Präzise: dies ist ein Überlagerungsraum (def. ) mit Blattmenge an jedem Punkt isomorph zur Menge $\mathbb{Z}$ der ganzen Zahlen.

Definition

(Wirkung der Fundamentalgruppe auf Blätter einer Überlagerung)

Sei $E \overset{\pi}{\longrightarrow} X$ ein Überlagerungsraum (def. ).

Dann gilt für jeden Punkt $x \in X$ und jede Wahl von Element $e \in F_x$ aus der Blattmenge über $x$, es existiert, bis auf Homotopie, eine eindeutige Hebung

• eines Pfades in $X$ der ein Element $\gamma$ der Fundamentalgruppe $\pi_1(X,x)$ (def. ) repräsentiert

• zu einem stetigen Pfad in $E$ der bei $e$ beginnt.

Dieser Pfad endet notwendigerwise and einem (anderen) Punkt

$$\rho_\gama(e) \in F_x$$

in derselben Faser.

Diese Kontruktion gibt eine Funktion

$$\array{ \rho &\colon& F_x \times \pi_1(X,x) &\longrightarrow& F_x \\ && (e,\gamma) &\mapsto& \rho_\gamma(e) }$$

aus dem kartesischen Produk des Blattraumes mit der Fundamentalgruppe. Diese Funtion ist kompatibel mit der Gruppen-Struktur auf $\pi_1(X,x)$, in dem Sinne dass die folgenden Diagramme kommutieren:

$$\array{ F_x \times \{const_x\} && \longrightarrow && F_x \times \pi_1(X,x) \\ & {}_{\mathllap{id}}\searrow && \swarrow_{\mathrlap{\rho}} \\ && F_x } \;\;\;\;\;\; \left( \array{ \text{das neutrale Element,} \\ \text{also die konstante Schleife} \\ \text{wirkt trivial} } \right)$$

and

$$\array{ F_x \times \pi_1(X,x) \times \pi_1(X,x) &\overset{\rho \times id}{\longrightarrow}& F_x \times \pi_1(X,x) \\ {}^{\mathllap{id \times ((-)\cdot(-))}}\downarrow && \downarrow^{\mathrlap{\rho}} \\ F_x \times \pi_1(X,x) &\underset{\rho}{\longrightarrow}& F_x } \;\;\;\;\;\; \left( \array{ \text{die Wirkung von zwei Gruppenelementen } \\ \text{ist die gleiche wie} \\ \text{erst beide Elemente zu verknüpfen} \\ \text{und dann mit dem Produkt zu wirken} } \right) \,.$$

Man sagt auch dass $\rho$ eine Wirkung oder Permutationsdarstellung von $\pi_1(X,x)$ auf $F_x$ ist.

For $G$ irgend eine Gruppe, dann gibt es eine kategorie $G Set$ deren Objekte die Mengen mit $G$-Wirkung sind, und deren Morphismen solche Funktionen sind die diese $G$-Wirkung respektieren.

Die obige Konstruktion ist dann ein Funktor der Form

$$Cov(X) \longrightarrow \pi_1(X,x) Set \,.$$

Beispiel

(drei-blättrige Überdeckung des Kreises)

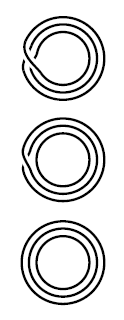
Es gibt, bis auf Isomorphismus, drei uterschiedliche 3-blättrige Überlagerungen des Kreises $S^1$.

Die von Beeispiel für $k = 3$. Und eine andere. Und die triviale. Die zugehörigen Permutationswirkungen sind in dem bild rechts angedeutet.

graphics grabbed from Hatcher

Wir sind jetzt bereit den Hauptsatz über die Fundamentalgruppe zu nennen.

Wir bnötigen nur noch die folgende technische Bdingung. Diese ist für alle “sinnvollen” topologischen Räume erfüllt:

Definition

(semi-lokal einfach zusammenhängend)

Ein topologischer Raum $X$ heisst

1. lokal pfad-zusammenhängend wenn für jeden Punkt $x \in X$ und für jede neighbourhoodUmgebung? $x \in U \subset X$ gilt dass eine Umgebung $x \in V \subset U$ existiert so dass $V$ pfad-zusammenhängend ist (def. );

2. semi-lokal einfach zusammenhängend wenn jeder Punkt $x \in X$ eine Umgebung $x \in U \subset X$ hat so dass der induzierte Morphismus von Fundamentalgruppen $\pi_1(U,x) \to \pi_1(X,x)$ trivial ist (also jedes Element auf das neutrale Element schickt).

Theorem

(Fundamentalsatz der Überlagerungstheorie)

Sei $X$ ein topologischer Raum der pfad-zusammenhängend (def. ), lokal pfad-zusammenhängend (def. ) und semi-lokal einfach zusammenhängend ist (def. ).

Dann ist für jedes $x \in X$ der Funktor

$$Fib_x \;\colon\; Cov(X) \overset{}{\longrightarrow} \pi_1(X,x) Set \,.$$

von def. der die Wirkung der Fundamentalgruppe von $X$ auf die Menge der Blätter über $x$ konstruiert hat die folgenden Eigenschaften:

1. jede Isomorphieklasse von $\pi_1(X,x)$-Wirkungen ist im Bild des Funktors (man sagt: der Funktor ist essentiell surjectiv);

2. für je zwei Überlagerungsräume $E_1, E_2$ of $X$ ist die Abbildung au Morphismen-Mengen

   $$Fib_x \;\colon\; Hom_{Cov(X)}(E_1, E_2) \longrightarrow Hom( Fib_x(E_1), Fib_x(E_2) )$$

   eine Bijektion (man sagt der Funktor ist voll true ).

Ein Funktor mit diesen Eigenschaften heisst Äquivalenz von Kategorien:

$$Cov(X) \overset{\simeq}{\longrightarrow} \pi_1(X,x) Set \,.$$

Dies hat einige interessante Konsequenzen…

$\,$

$\,$

Every sufficiently nice topological space $X$ as above has a covering which is simply connected (def. ). This is the covering corresponding, under the fundamental theorem of covering spaces (theorem ) to the action of $\pi_1(X)$ on itself. This is called the universal covering space $\hat X \to X$. The above theorem implies that the fundamental group itself may be recovered as the automorphisms of the universal covering space:

$$\pi_1(X) \simeq Aut_{Cov_{/X}}(\hat X, \hat X) \,.$$

Example

(computing the fundamental group of the circle)

The covering $\exp(2\pi i(-)) \;\colon\; \mathbb{R}^1 \to S^1$ from example is simply connected (def. ), hence must be the universal covering space, up to homeomorphism.

It is fairly straightforward to see that the only homeomorphisms from $\mathbb{R}^1$ to itself over $S^1$ are given by integer translations by $n \in \mathbb{N} \hookrightarrow \mathbb{R}$:

$$\array{ \mathbb{R}^1 && \underoverset{\simeq}{t \mapsto t + n}{\longrightarrow} && \mathbb{R}^1 \\ & {}_{\mathllap{\exp(2 \pi i(-))}}\searrow && \swarrow_{\mathrlap{\exp(2 \pi i(-))}} \\ && S^1 } \,.$$

Hence

$$Aut_{Cov_{/S^1}}(\hat S^1, \hat S^1) \simeq \mathbb{Z}$$

and hence the fundamental group of the circle is the additive group of integers:

$$\pi_1(S^1) \simeq \mathbb{Z} \,.$$

$\,$

---

$\,$

Literatur

Einführende Lehrbücher:

• James Munkres, Topology, Prentice Hall 1975 (2000)

• Terry Lawson, Topology: A Geometric Approach, Oxford University Press (2003) (pdf)

Siehe auch die Literatur unter algebraische Topologie.

Kurzeinführungen:

• Friedhelm Waldhausen, Topologie (pdf)

• Alex Kuronya, Introduction to topology, 2010 (pdf)

• Anatole Katok, Alexey Sossinsky, Introduction to modern topology and geometry (pdf)

Siehe auch

• Topospaces, ein Wiki mit Grundlagen zur Topologie.