nLab homotopy groups of spheres
Context
Spheres
Homotopy theory
homotopy theory, (∞,1)-category theory, homotopy type theory
flavors: stable, equivariant, rational, p-adic, proper, geometric, cohesive, directed…
models: topological, simplicial, localic, …
see also algebraic topology
Introductions
Definitions
Paths and cylinders
Homotopy groups
Basic facts
Theorems
Stable Homotopy theory
Ingredients
Contents
Homotopy groups of spheres
My initial inclination was to call this book The Music of the Spheres, but I was dissuaded from doing so by my diligent publisher, who is ever mindful of the sensibilities of librarians. (D. Ravenel 86, preface)
With all due respect to anyone interested in them, the stable homotopy groups of spheres are a mess. (J. F. Adams 74, p 204)
Idea
The homotopy groups of spheres are the homotopy classes of maps
For fixed , the colimit over with respect to the suspension homomorphism
over all (called the -stem) is called the stable homotopy groups of spheres (also: the “stable -stem”)
In fact, by the Freudenthal suspension theorem, the value of the stabilizes for (depend only on in this range), whence the name.
The stable homotopy groups of sphere are equivalently the homotopy groups of a spectrum for the sphere spectrum
The stable homotopy groups of spheres are notorious for their immense computational richness. Many of the tools of algebraic topology and stable homotopy theory were devised to compute more and more of the stable stems. This notably include the Adams spectral sequence, the Adams-Novikov spectral sequence.
Tables
The first few stable homotopy groups of the sphere spectrum are
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
The following tables show the p-primary decomposition of these and the following stable homotopy groups.
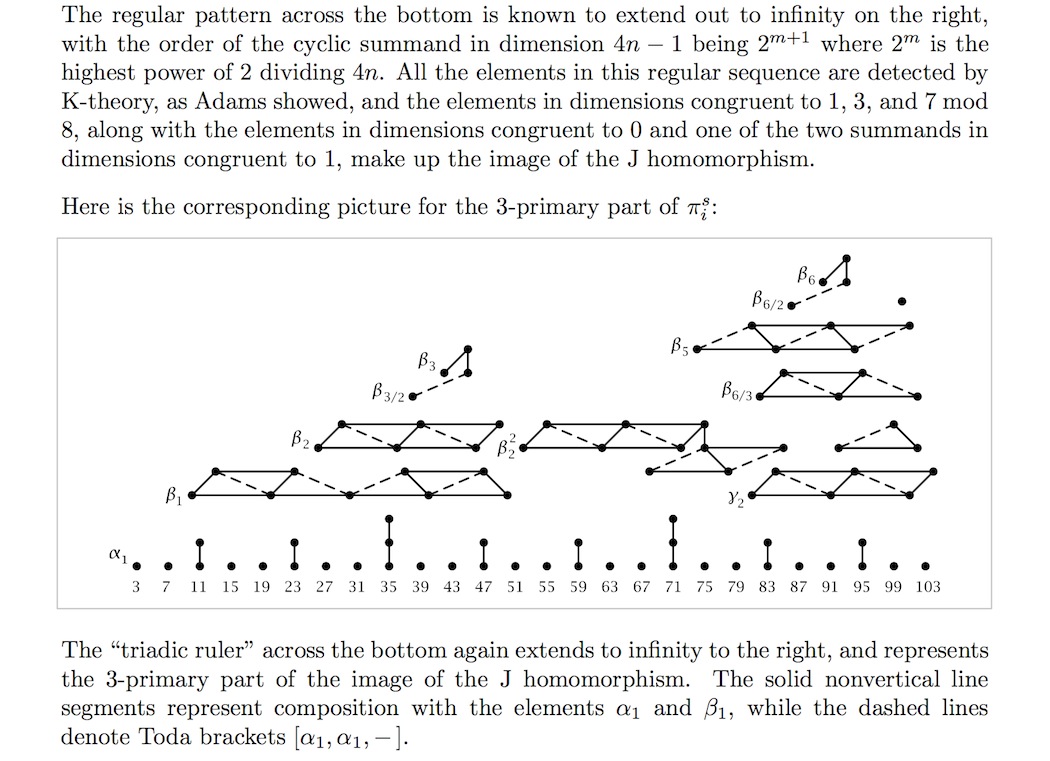
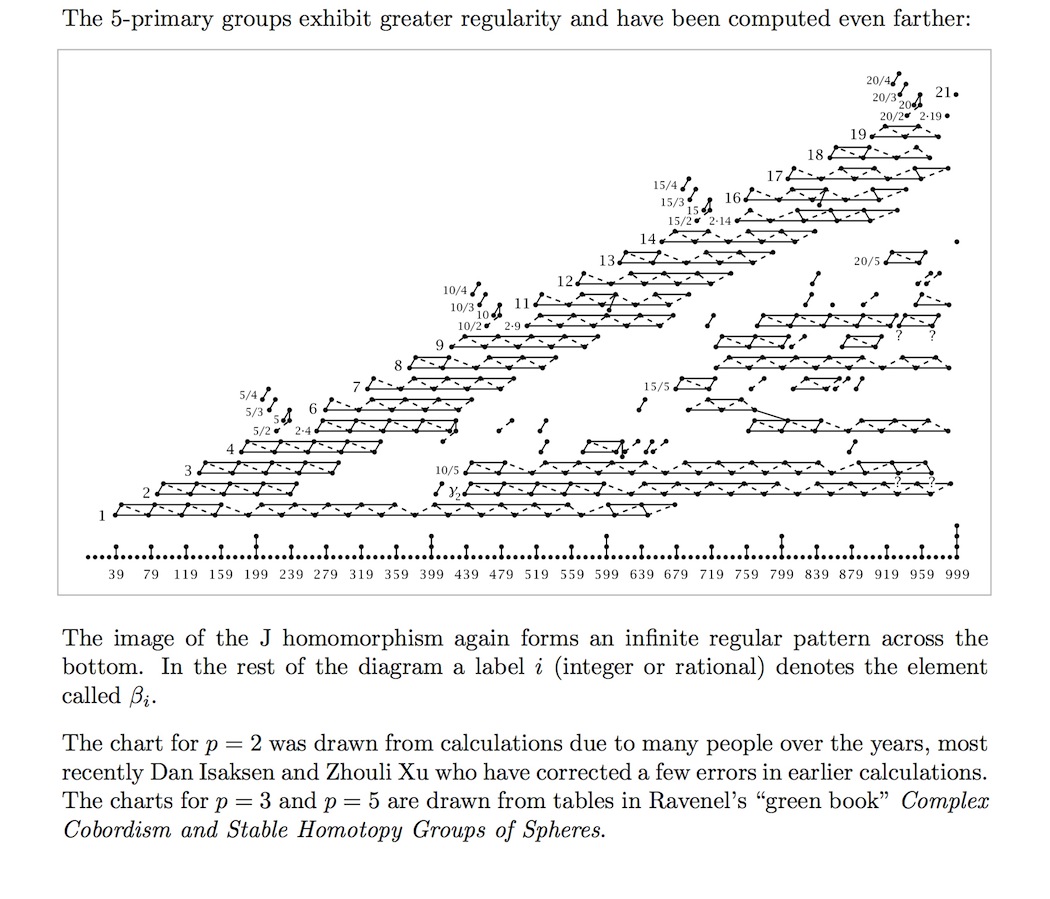
The horizontal index is the degree of the stable homotopy group . The appearance of a string of connected dots vertically above index means that there is a direct summand primary group of order . The bottom rows in each case are given by the image of the J-homomorphism.
See at fundamental theorem of finitely generated abelian grouops – Graphical representation for details on the notation used in these table, and see example below for illustration.
(the following graphics are taken from Hatcher, based on (Ravenel 86)
-primary component

-primary component
-primary component
Example
The finite abelian group decomposes into primary groups as . Here corresponds to the three dots above in the first table, and to the single dot over in the second.
The finite abelian group decomposes into primary groups as . Here corresponds to the four dots above in the first table, and to the single dot over in the second and to the single dot over in the third table.
Examples
0th stem
See at Hopf degree theorem.
1st stem
The first stable homotopy group of spheres (the first stable stem) is the cyclic group of order 2:
where the generator is represented by the complex Hopf fibration .
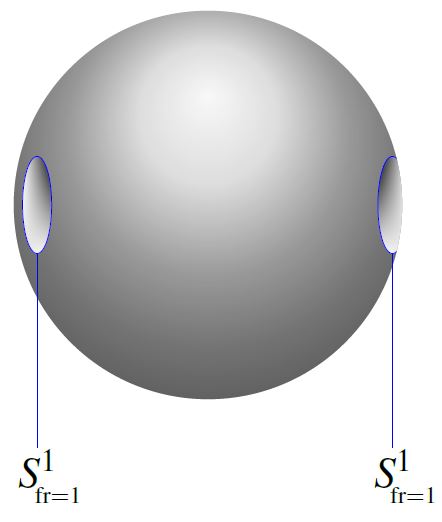
Under the Pontrjagin-Thom isomorphism, identifying the stable homotopy groups of spheres with the bordism ring of stably framed manifolds (see at MFr), the generator (1) is represented by the 1-sphere (with its left-invariant framing induced from the identification with the Lie group U(1))
Moreover, the relation is represented by the bordism which is the complement of 2 open balls inside the 2-sphere.
2nd stem
The second stable homotopy group of spheres…
3rd stem
The third stable homotopy group of spheres (the third stable stem) is the cyclic group of order 24:
where the generator is represented by the quaternionic Hopf fibration .
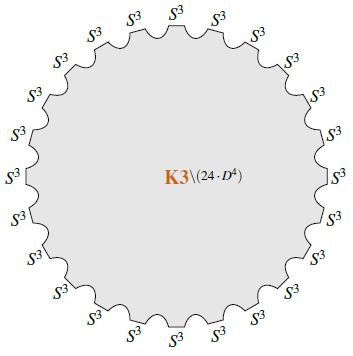
Under the Pontrjagin-Thom isomorphism, identifying the stable homotopy groups of spheres with the bordism ring of stably framed manifolds (see at MFr), the generator (2) is represented by the 3-sphere (with its left-invariant framing induced from the identification with the Lie group SU(2) Sp(1) )
Moreover, the relation is represented by the bordism which is the complement of 24 open balls inside the K3-manifold (e.g. Wang-Xu 10, Sec. 2.6, Bauer 10, SP 17).
Equivalently, the elements of are detected by half the Todd classes of cobounding manifolds with special unitary group-tangential structure on their stable tangent bundle (elements of the MSUFr-bordism ring):
We have the following short exact sequence of the MSU-, MSUFr- and MFr-bordism rings (Conner-Floyd 66, p. 104)
which produces from half the Todd class of cobounding -manifolds the KO-theoretic Adams e-invariant (Adams 66, p. 39) of the boundary manifold in . For this detects the third stable homotopy group of spheres, by the following:
Proposition
(Adams 66, Example 7.17 and p. 46)
In degree 3, the KO-theoretic e-invariant takes the value on the quaternionic Hopf fibration and hence reflects the full third stable homotopy group of spheres:
while sees only “half” of it (by Adams 66, Prop. 7.14).
Properties
Serre finiteness theorem
Theorem
The homotopy group is a finite group except
-
for in which case ;
-
and in which case
for a finite group.
(Serre 53, see Ravenel 86, Chapter I, Lemma 1.1.8)
Nishida nilpotence theorem
The Nishida nilpotence theorem…
Relation to the framed bordism ring
By Thom's theorem, for any (B,f)-structure , there is an isomorphism (of commutative rings)
from the cobordism ring of manifolds with stable normal -structure to the homotopy groups of the universal -Thom spectrum.
Now for framing structure, then
is equivalently the sphere spectrum. Hence in this case Thom's theorem states that there is an isomorphism
between the framed cobordism ring and the stable homotopy groups of spheres.
For discussion of computation of this way, see for instance (Wang-Xu 10, section 2) and (Putnam).
For instance
-
because there are two -framings on a single point, corresponding to , the negative of a point with one framing is the point with the other framing, and so under disjoint union, the framed points form the group of integers;
-
because the only compact connected 1-manifold is the circle, there are two framings on the circle, corresponding to and they are their own negatives.
J-homomorphism and Adams e-invariant
The following characterizes the image of the J-homomorphism
from the homotopy groups of the stable orthogonal group to the stable homotopy groups of spheres. This was first conjectured in (Adams 66) (since called the Adams conjecture) and then proven in (Quillen 71).
Remark
By the discussion at orthogonal group – homotopy groups we have that the homotopy groups of the stable orthogonal group are
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 |
Because all groups appearing here and in the following are cyclic groups, we instead write down the order
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|---|
| 2 | 2 | 1 | 1 | 1 | 1 |
Theorem
The stable homotopy groups of spheres are the direct sum of the (cyclic) image of the J-homomorphism, and the kernel of the Adams e-invariant.
Moreover,
-
for and and positive the J-homomorphism is injective, hence its image is ,
-
for and hence for , the order of the image is equal to the denominator of , where is the Bernoulli number
-
for all other cases the image is necessarily zero.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Whitehead tower of orthogonal group | orientation | spin group | string group | fivebrane group | ninebrane group | |||||||||||||
| higher versions | special orthogonal group | spin group | string 2-group | fivebrane 6-group | ninebrane 10-group | |||||||||||||
| homotopy groups of stable orthogonal group | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||||||
| stable homotopy groups of spheres | 0 | 0 | 0 | |||||||||||||||
| image of J-homomorphism | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Related concepts
References
General
Introductions and surveys:
-
Alex Wright, Homotopy groups of spheres: A very basic introduction (pdf)
-
Guozhen Wang, Zhouli Xu, A survey of computations of homotopy groups of Spheres and Cobordisms, 2010 (pdf, pdf)
-
Andrew Putman, Homotopy groups of spheres and low-dimensional topology ([pdf]https://www3.nd.edu/~andyp/notes/HomotopySpheresLowDimTop.pdf), pdf)
-
Allen Hatcher, Pictures of stable homotopy groups of spheres (html)
-
Mark Mahowald, Doug Ravenel, Towards a Global Understanding of the Homotopy Groups of Spheres, in: Samuel Gitler (ed.): The Lefschetz Centennial Conference: Proceedings on Algebraic Topology II, Contemporary Mathematics volume 58, AMS 1987 (pdf, pdf, ISBN:978-0-8218-5063-3)
-
Haynes Miller, Doug Ravenel, Mark Mahowald’s work on the homotopy groups of spheres (pdf)
-
Doug Ravenel, Complex cobordism and stable homotopy groups of spheres, since 1986 (web)
-
Stanley Kochmann, Stable Homotopy Groups of Spheres – A Computer-Assisted Approach, Lecture Notes in Mathematics, 1990
-
Doug Ravenel, Nilpotence and Periodicity in Stable Homotopy Theory, Annals of Mathematics Studies 128, Princeton University Press (1992) [ISBN:9780691025728, pdf, webpage]
-
Stanley Kochmann, section 5 of of Bordism, Stable Homotopy and Adams Spectral Sequences, AMS 1996
-
Daniel Isaksen, Guozhen Wang, Zhouli Xu, Stable homotopy groups of spheres, PNAS October 6, 2020 117 (40) 24757-2476 (arXiv:2001.04247, doi:10.1073/pnas.2012335117)
-
Daniel Isaksen, Guozhen Wang, Zhouli Xu, More stable stems (arXiv:2001.04511)
A tabulation of stable homotopy groups of spheres is in
- Doug Ravenel, Appendix 3 of Complex cobordism and stable homotopy groups of spheres (pdf)
Original articles on basic properties:
- Jean-Pierre Serre, Groupes d’homotopie et classes de groupes abelien, Ann. of Math. 58 (1953), 258–294 (jstor:1969789)
Early computation of unstable homotopy groups of spheres up to :
- Hirosi Toda, Composition Methods in Homotopy Groups of Spheres, Annals of Mathematics Studies Vol. 49, Princeton University Press (1962) (jstor:j.ctt1bgzb5t)
See also:
-
Wikipedia, Homotopy groups of spheres
-
MathOverflow: Computational complexity of computing homotopy groups of spheres [MO:q/31004]
-
Prasit Bhattacharya, Irina Bobkova, J. D. Quigley: New infinite families in the stable homotopy groups of spheres (2024) [arXiv:2404.10062]
Expressing the homotopy groups of the 2-sphere in terms of Brunnian braid groups:
- A. J. Berrick, Frederick R. Cohen, Y. L. Wong and J. Wu: Configurations, braids, and homotopy groups, J. Amer. Math. Soc. 19 (2006) 265-326 [doi:10.1090/S0894-0347-05-00507-2, pdf]
On presentation of homotopy groups of the 2-sphere as centers of certain groups with finite presentations:
- Roman Mikhailov, Jie Wu. A combinatorial description of homotopy groups of spheres (2011). (arXiv:1108.3055).
On nontriviality of homotopy groups of the 2-sphere:
- Roman Mikhailov, Sergey Ivanov. On nontriviality of homotopy groups of spheres (2015). (arXiv:1506.00952).
Image of the J-homomorphism
Discussion of the image of the J-homomorphism is due to
-
John Adams, On the groups IV, Topology 5: 21,(1966) Correction, Topology 7 (3): 331 (1968)
-
Daniel Quillen, The Adams conjecture, Topology. an International Journal of Mathematics 10: 67–80 (1971)
Formalization in homotopy type theory
For formalization in homotopy type theory see
-
formalization of the homotopy groups of spheres in homotopy type theory
-
Guillaume Brunerie, On the homotopy groups of spheres in homotopy type theory (arXiv:1606.05916)
Last revised on December 21, 2024 at 15:47:07. See the history of this page for a list of all contributions to it.