nLab light-cone quantization

Skip the Navigation Links | Home Page | All Pages | Latest Revisions | Discuss this page |
Contents

Context

Physics

physics, mathematical physics, philosophy of physics

Surveys, textbooks and lecture notes

theory (physics), model (physics)

experiment, measurement, computable physics

Contents

Idea

General

In Hamiltonian formulation of relativistic quantum field theory on Minkowski spacetime there are three essential choices of forms of hypersurfaces to foliate spacetime by [Dirac (1949)]:

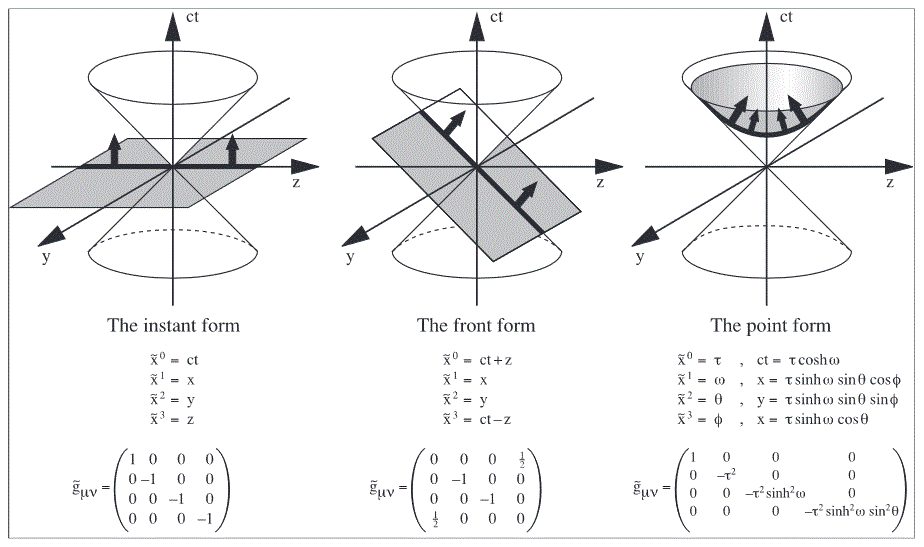
(Fig. 1 from Brodsky, Pauli & Pinsky (1998))

The “instant form” on the left foliates spacetime by spacelike hypersurfaces (cf. Cauchy surface). This is the form considered for Hamiltonian mechanics in most of the literature (certainly in the case of quantum mechanics, cf. [Dirac (1949) §3]).

In contrast, light-cone quantization corresponds to the choice of foliation by lightlike wavefronts [Dirac (1949) §5].

Dirac (1949) §8:

The instant form has the advantage of being the one people are most familiar with, but I do not believe it is intrinsically any better for this reason. […]

The front form has the advantage that it requires only three Hamiltonians, instead of the four of the other forms. This makes it mathematically the most interesting form, and makes any problem of finding Hamiltonians substantially easier.

The front form has the further advantage that there is no square root in the Hamiltonians, which means that one can avoid negative energies for particles by suitably choosing the values of the dynamical variables in the front, without having to make a special convention about the sign of a square root.

(…)

Discretized light-cone quantization

For non-perturbative computations it turns out at least convenient (if not necessary) to in addition assume/impose periodic boundary conditions along the lightlike front, hence, in flat lightcone coordinates x ±x^{\pm}, so that all fields ϕ\phi satisfy

ϕ(x −+L,x +)=ϕ(x −,x +) \phi\big( x^- + L,\, x^+ \big) \;=\; \phi\big( x^-,\, x^+ \big)

for some L∈ℝ >0L \in \mathbb{R}_{\gt 0} giving the circumference of a lightlike circle (which some authors take to be literally lightlike, of the kind shown eg. in Bär 2004, Exp. 2.21 (2), while others, like Seiberg 1997, consider to be the limit of boosts of a spacelike circle fiber).

Since, dually, this means that the corresponding lightcone momentum p +p^+ becomes quantized in units of the inverse radius RR of this circle

(1)p +∝N/RAAAN∈ℤ, p^+ \;\propto\; N/R \phantom{AAA} N \in \mathbb{Z} \,,

hence one speaks of discretized light-cone quantization or DLCQ, for short. This goes back to Maskawa & Yamakawi 1976; Casher 1976; Thorn 1977, 1978; Pauli & Brodsky (1985b), (1985a); Tang, Brodsky & Pauli 1991 (2.6); see also McCartor & Robertson 1994, §3; for review see Burkardt 1996, §5.1; Heinzl 2001, §3.4.

Often it turns out that negative values of NN in (1) can be neglected or integrated out, so that

N∈ℕ N \in \mathbb{N}

becomes a natural number-parameter akin to that considered in the 't Hooft double line construction of gauge theories, and then the large N limit of the discrete light cone quantization becomes of interest.

For sigma-models

In quantization of sigma models whose target space has a lightlike Killing vector, the strategy of light-cone gauge quantization is to gauge fix the metric and diffeomorphisms of the worldvolume such that also the worldvolume has a lightlike Killing vector field and such that this is mapped to the given one on target space.

This typically fixes most of the available gauge freedom, and the strategy is then to apply quantization to what remains. For more on this general idea see at quantization commutes with reduction.

Often this is considered for target space being Minkowski spacetime ℝ d−1,1\mathbb{R}^{d-1,1} and with X +≔X 0−X 1X^+ \coloneqq X^0 - X^1 denoting one of its canonical lightlike coordinates. If τ\tau denotes similarly a lightlike coordinate function on the worldvolume, then the condition of light-cone gauge reads

X +=p +τ X^+ = p^+ \tau

for some proportionality constant p +p^+, the light cone momentum. This is how light cone gauge appears in much of the string theory literature.

Applications

Quantization of Green-Schwarz super pp-brane sigma models

Light cone gauge quantization is the only method by which Green-Schwarz super p-brane sigma models have been quantized, to date.

BFSS matrix model

Specifically, applying light-cone gauge quantization to the Green-Schwarz sigma model for the M2-brane on 11d Minkowski spacetime, combined with a certain regularization of the remaining light-cone Hamiltonian yields the BFSS matrix model.

BMN matrix model

Alternatively, applying the light cone gauge quantization of the Green-Schwarz sigma-model of the M2-brane not on Minkowski spacetime but, more generally, on 11d pp-wave spacetimes (which are Penrose limits of the near horizon geometry of the black M2-branes/M5-branes) yields the BMN matrix model.

References

General

The concept originates with

reviewed in

  • K. K. Wan, J. J. Powis, Quantum mechanics in Dirac’s front form, Int J Theor Phys 33 (1994) 553–574 [doi:10.1007/BF00670516]

and was rediscovered several times, such as in the guise of “infinite momentum frame” field theory:

see also Chang & Ma 1969 and Kogut & Soper 1970

Early review:

Further review:

See also:

The notion of lightlike circle compactification (“discretized light-cone quantization”):

and on the issue of excluding p +=0p^+ = 0:

See also:

Lecture notes:

More on the case of gauge fields:

In relation to spontaneous symmetry breaking:

In relation to instant-time quantization:

Discussion of (reduced) phase spaces in light-cone coordinates:

Application to quantum electrodynamics

Application to quantum electrodynamics:

and to pure electromagnetism:

Application to quantum chromodynamics

Application of (discretized) light cone quantization to to QCD:

Review in the broader context of non-perturbative quantum field theory:

A light-cone QCD-Lagrangian density adapted to MHV amplitudes:

  • Hiren Kakkad, Piotr Kotko, Anna Stasto, Quantum correction to a new Wilson line-based action for Gluodynamics [arXiv:2311.04101]

Application in string theory

Light cone quantization of the string sigma-model originates with

see also

All the standard introductory texts on string theory have sections devoted to light-cone quantization. For instance:

In the context of the BFSS matrix model as a discrete light-cone formulation of M-theory:

Review:

Quantization of the M2-brane sigma-model to a matrix model

The Poisson bracket-formulation of the classical light-cone gauge Hamiltonian for the bosonic relativistic membrane and the corresponding matrix commutator regularization is due to:

Some exact solutions:

On the regularized light-cone gauge quantization of the Green-Schwarz sigma model for the M2-brane on (super) Minkowski spacetime, yielding the BFSS matrix model:

Original articles:

Observation that the spectrum is continuous:

Review:

The generalization to pp-wave spacetimes (leading to the BMN matrix model):

See also

A new kind of perturbation series for the quantized super-membrane:

Relation to the string dilaton under double dimensional reduction:

Last revised on January 29, 2024 at 06:16:14. See the history of this page for a list of all contributions to it.

EditDiscussPrevious revisionChanges from previous revisionHistory (29 revisions) Cite Print Source