nLab Tully-Fisher relation
Note: Tully-Fisher relation and Tully-Fisher relation both redirect for "mass-discrepancy acceleration relation".
Context
Physics
physics, mathematical physics, philosophy of physics
Surveys, textbooks and lecture notes
theory (physics), model (physics)
experiment, measurement, computable physics
-
-
-
Axiomatizations
-
Tools
-
Structural phenomena
-
Types of quantum field thories
-
Gravity
Formalism
Definition
Spacetime configurations
Properties
Spacetimes
| black hole spacetimes | vanishing angular momentum | positive angular momentum |
|---|---|---|
| vanishing charge | Schwarzschild spacetime | Kerr spacetime |
| positive charge | Reissner-Nordstrom spacetime | Kerr-Newman spacetime |
Quantum theory
Contents
Idea
In astronomy, the Tully-Fisher relation is a relation between the asymptotic behaviour of galaxy rotation curves, witnessed by the width of their 21cm hydrogen line, and the total visible baryonic mass of the galaxies.
For most observed galaxies their rotation curves do not follow the predictions of standard gravity applied to the visible baryonic mass distribution in the galaxy. This has led to the speculation that either there is further invisible but gravitating dark matter making up most of the mass of galaxies, or the laws of gravity are modified on galactic scales (“MOND”).
Recent computer simulation (FIRE) of galactic structure formation using the standard cold dark matter model qualitatively reproduces the peculiar galactic rotation curves that motivated dark matter (or MOND, for that matter) in the first place (Hopkins et al. 17, Figure 4, Figure 5):
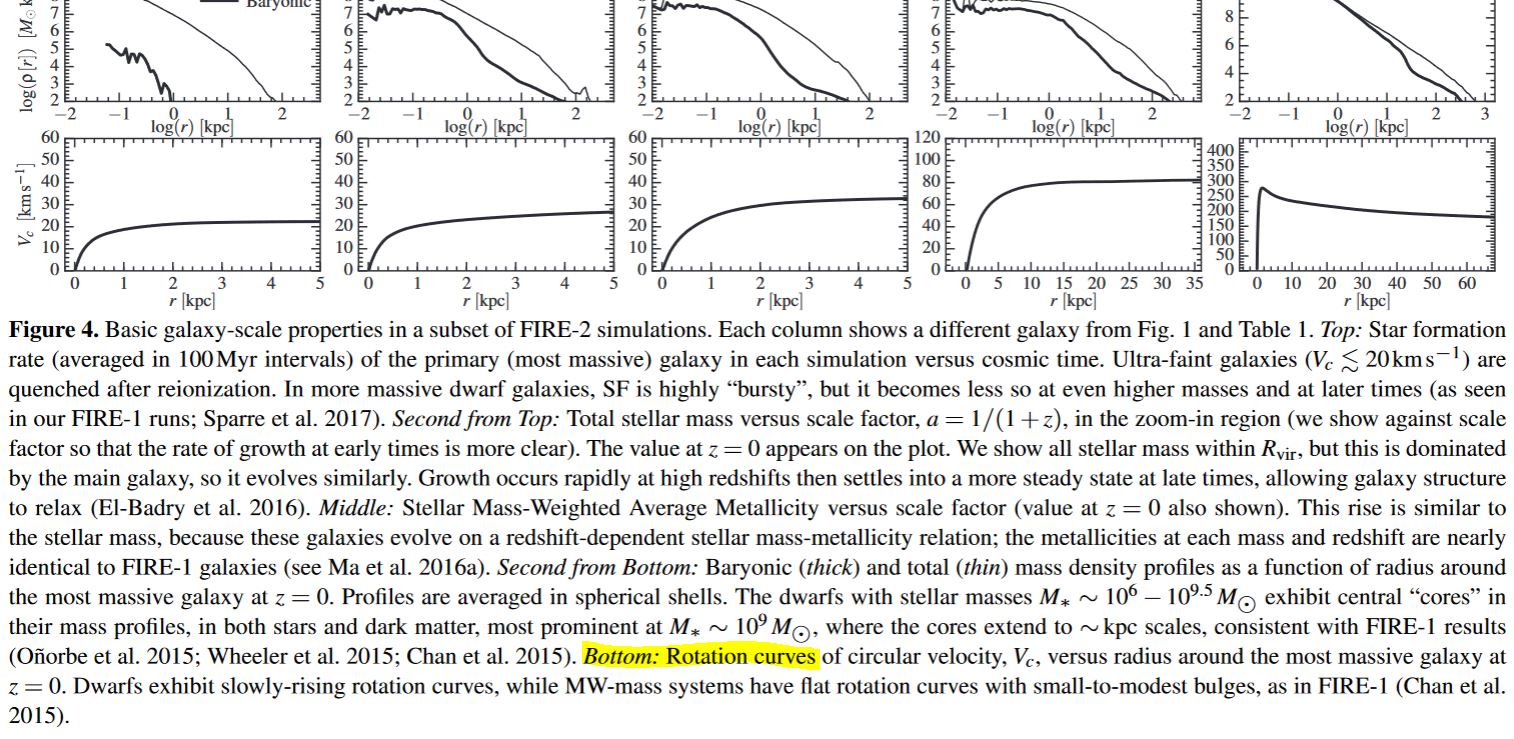
graphics grabbed from (Hopkins et al. 17)
and also reproduces well the baryonic Tully-Fisher relation (El-Badry et al. 18, Figure 4) which used to be an issue in the standard cold dark matter model:
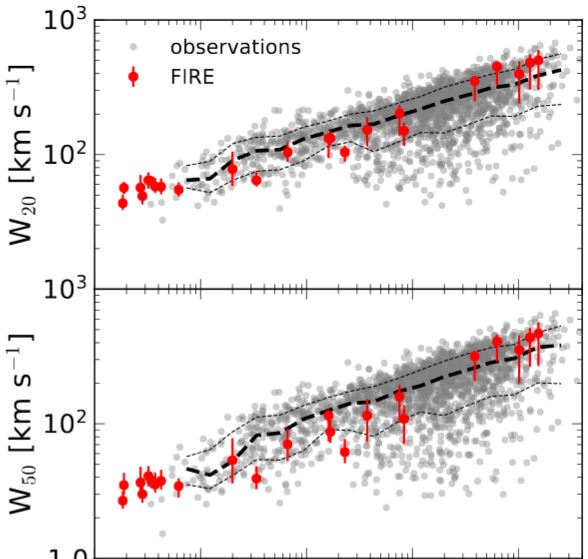
graphics grabbed from (El-Badry et al. 18)
More in detail, galaxy rotation curves exhibit a close correlation between angular velocity and total visible enclosed math at any given radius, called the radial acceleration relation (RAR) or mass-discrepancy acceleration relation. This, too, is reproduced in cold dark matter-model (in theoretical physics) computer simulation (Santos-Santos et al. 15, Cintio-Lelli 15, Keller-Wadsley 16, Ludlow et al 16). These early simulations were not found conclusive in Lelli et al 16, section 8.2. But more detailed analysis (PSF 18) and more refined simulation Dutton-Maccio-Obreja-Buck 19 has then been claimed to confirm the statement.
A conceptual explanation via stellar feedback is discussed in GBFH19.
References
See also
- Wikipedia, Tully-Fisher relation
Computer simulation of dark matter structure formation on galaxy-scales
-
Hopkins et al. FIRE-2 Simulations: Physics versus Numerics in Galaxy Formation. Monthly Notices of the Royal Astronomical Society, Volume 480, Issue 1, 11 October 2018, Pages 800–863 (arXiv:1702.06148, doi:10.1093/mnras/sty1690)
-
El-Badry et al. Gas Kinematics in FIRE Simulated Galaxies Compared to Spatially Unresolved HI Observations, Monthly Notices of the Royal Astronomical Society, Volume 477, Issue 2, 21 June 2018, Pages 1536–1548 (arXiv:1801.03933, doi:10.1093/mnras/sty730)
On the mass-discrepancy acceleration relation:
-
Arianna Di Cintio, Federico Lelli, The mass discrepancy acceleration relation in a context, Monthly Notices of the Royal Astronomical Society: Letters, Volume 456, Issue 1, 11 February 2016, Pages L127–L131 (arXiv:1511.06616, doi:10.1093/mnrasl/slv185)
-
Isabel M. Santos-Santos et al. The distribution of mass components in simulated disc galaxies (arXiv:1510.02474)
-
B.W. Keller, J.W. Wadsley, is Consistent with SPARC Radial Acceleration Relation (arXiv:1610.06183)
-
Aaron D. Ludlow et. al. The Mass-Discrepancy Acceleration Relation: a Natural Outcome of Galaxy Formation in Cold Dark Matter halos, Phys. Rev. Lett. 118, 161103 (2017) (arXiv:1610.07663)
-
Chiara Di Paolo, Paolo Salucci, Jean Philippe Fontaine, The Radial Acceleration Relation (RAR): the crucial cases of Dwarf Discs and of Low Surface Brightness galaxies, ApJ 2019 (arXiv:1810.08472)
-
Aaron A. Dutton, Andrea V. Macciò, Aura Obreja, Tobias Buck, NIHAO XVIII: Origin of the MOND phenomenology of galactic rotation curves in a LCDM universe (arXiv:1902.06751)
Critical comments on the early simulations in
- Federico Lelli, Stacy S. McGaugh, James M. Schombert, Marcel S. Pawlowski, section 8.2 of One Law To Rule Them All: The Radial Acceleration Relation of Galaxies (arXiv:1610.08981)
Conceptual explanation via stellar feedback:
- Michael Y. Grudić, Michael Boylan-Kolchin, Claude-André Faucher-Giguère, Philip Hopkins?, Stellar feedback sets the universal acceleration scale in galaxies (arxiv:1910.06345)
Last revised on October 16, 2019 at 18:28:22. See the history of this page for a list of all contributions to it.