nLab super 1-brane in 3d
Context
String theory
Ingredients
Critical string models
Extended objects
Topological strings
Backgrounds
Phenomenology
Super-Geometry
superalgebra and (synthetic ) supergeometry
Background
Introductions
Superalgebra
Supergeometry
Supersymmetry
Supersymmetric field theory
Applications
Contents
Idea
By the brane scan there exists a classical (pre-quantum) Green-Schwarz super p-brane sigma model for (superstrings) with target space being dimensional super Minkowski spacetime or more generally a superspacetime which is a super Cartan geometry solving the equations of motion of or 3d supergravity. (The literature traditionally knows this as the “3d superstring”.)
For this is the double dimensional reduction of the super 2-brane in 4d (e.g. Mezincescu-Townsend 11, p. 44).
These superstrings in 3d target spacetime play a role in the AdS3-CFT2 and CS-WZW correspondence (e.g. (YuZ-Zhang 98)) and at least after a topological twist as exhibiting 3d Chern-Simons theory as a second quantization (see at TCFT – Effective background theories).
Quantization
While the light-cone gauge quantization of the Green-Schwarz superstrings breaks Lorentz group-symmetry for and , it preserves Lorentz symmetry not only for (the “critical string” of heterotic string theory or type II string theory) but also for (Mezincescu-Townsend 10, Mezincescu-Townsend 11). This quantization turns out to be equivalent to that of the RR-sector of the worldsheet supersymmetric spinning string in (Mezincescu-Routh-Townsend 13).
Related concepts
The brane scan.
The Green-Schwarz type super -brane sigma-models (see at table of branes for further links and see at The brane bouquet for the full classification):
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 11 | M2 | M5 | ||||||||
| 10 | D0 | F1, D1 | D2 | D3 | D4 | NS5, D5 | D6 | D7 | D8 | D9 |
| 9 | * | |||||||||
| 8 | * | |||||||||
| 7 | M2 | |||||||||
| 6 | F1, S1 | S3 | ||||||||
| 5 | * | |||||||||
| 4 | * | * | ||||||||
| 3 | * |
(The first columns follow the exceptional spinors table.)
The corresponding exceptional super L-∞ algebra cocycles (schematically, without prefactors):
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 11 | on sIso(10,1) | on m2brane | ||||||||
| 10 | on sIso(9,1) | on StringIIA | on StringIIB | on StringIIA | on sIso(9,1) | on StringIIA | on StringIIB | in StringIIA | on StringIIB | |
| 9 | on sIso(8,1) | |||||||||
| 8 | on sIso(7,1) | |||||||||
| 7 | on sIso(6,1) | |||||||||
| 6 | on sIso(5,1) | on sIso(5,1) | ||||||||
| 5 | on sIso(4,1) | |||||||||
| 4 | on sIso(3,1) | on sIso(3,1) | ||||||||
| 3 | on sIso(2,1) |
The Brane molecule
Furthermore, there exists a more general classification of possible supermembranes in spacetime with spatial dimensions and time dimensions, appearing in (Blencowe-Duff 88). In this sense, the brane scan is but the branch of the brane molecule. The objects appearing here are expected to be related to other generalizations of string theory. See D=12 supergravity and bosonic M-theory.
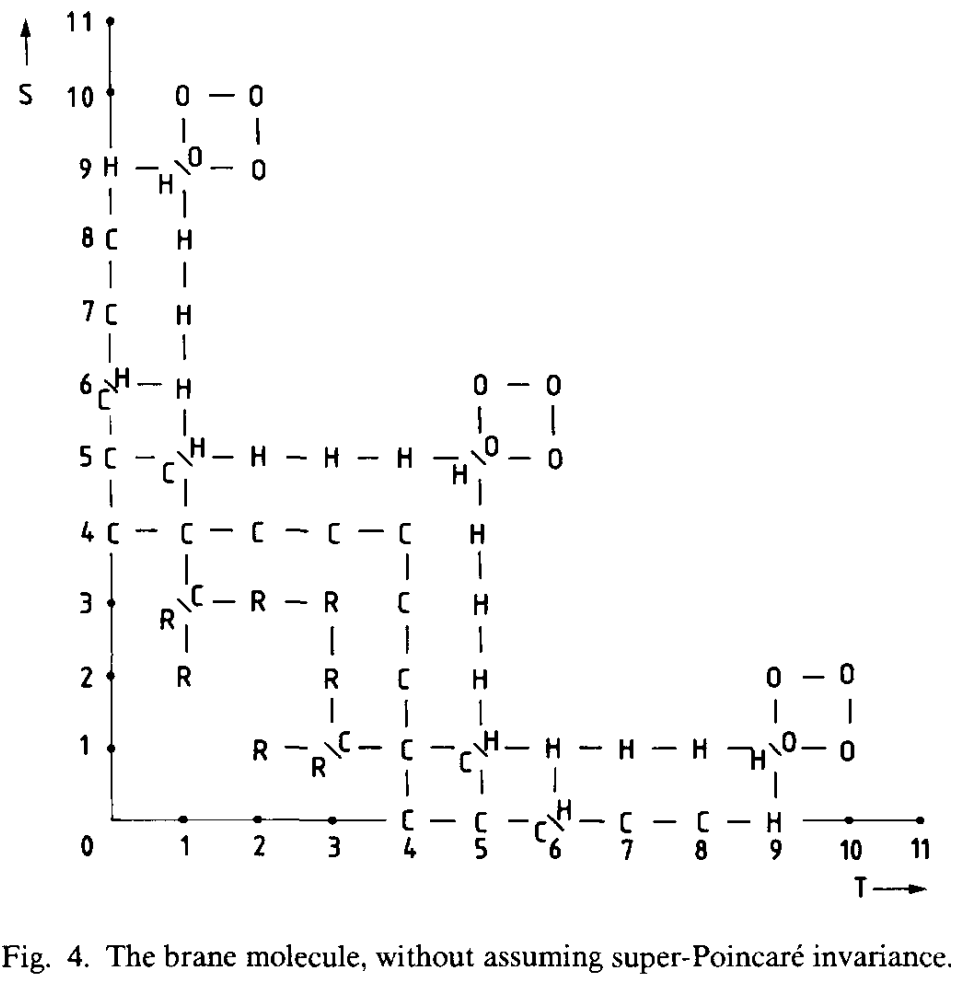
Compare:
-
Miles Blencowe, Mike Duff, Supermembranes and the Signature of Space-time, Nucl. Phys. B310 (1988) 387-404 (spire:262142, 10.1016/0550-3213(88)90155-1, pdf)
References
-
Ming Yu, Bo Zhang, Light-Cone Gauge Quantization of String Theories on AdS3 Space, Nucl.Phys. B551 (1999) 425-449 (arXiv:hep-th/9812216)
-
Luca Mezincescu, Paul Townsend, Anyons from Strings, Phys.Rev.Lett.105:191601,2010 (arXiv:1008.2334)
-
Luca Mezincescu, Paul Townsend, Quantum 3D Superstrings, PhysRevD.84.106006 (arXiv:1106.1374)
-
Luca Mezincescu, Alasdair J. Routh, Paul Townsend, Equivalence of 3D Spinning String and Superstring, J. High Energ. Phys. (2013) 2013: 24 (arXiv:1305.5049)
The F-theory-lift of the 3d superstring is discussed in
- William D. Linch III, Warren Siegel, F-theory Superspace (arXiv:1501.02761)
Last revised on January 15, 2019 at 14:03:32. See the history of this page for a list of all contributions to it.