nLab electron propagator

Idea

In quantum field theory, specifically in the discussion of quantum electrodynamics, the Feynman propagator for the free Dirac field modeling the electron is often called the electron propagator.

Example

(Feynman amplitudes in causal perturbation theory – example of QED)

In perturbative quantum field theory, Feynman diagrams are labeled multigraphs that encode products of Feynman propagators, called Feynman amplitudes (this prop.) which in turn contribute to probability amplitudes for physical scattering processes – scattering amplitudes:

The Feynman amplitudes are the summands in the Feynman perturbation series-expansion of the scattering matrix

$$\mathcal{S} \left( S_{int} \right) = \underset{k \in \mathbb{N}}{\sum} \frac{1}{k!} \frac{1}{(i \hbar)^k} T( \underset{k \, \text{factors}}{\underbrace{S_{int}, \cdots , S_{int}}} )$$

of a given interaction Lagrangian density $L_{int}$.

The Feynman amplitudes are the summands in an expansion of the time-ordered products $T(\cdots)$ of the interaction with itself, which, away from coincident vertices, is given by the star product of the Feynman propagator $\Delta_F$ (this prop.), via the exponential contraction

$$T(S_{int}, S_{int}) \;=\; prod \circ \exp \left( \hbar \int \Delta_{F}^{a b}(x,y) \frac{\delta}{\delta \mathbf{\Phi}^a(x)} \otimes \frac{\delta}{\delta \mathbf{\Phi}(y)} \right) ( S_{int} \otimes S_{int} ) \,.$$

Each edge in a Feynman diagram corresponds to a factor of a Feynman propagator in $T( \underset{k \, \text{factors}}{\underbrace{S_{int} \cdots S_{int}}} )$, being a distribution of two variables; and each vertex corresponds to a factor of the interaction Lagrangian density at $x_i$.

For example quantum electrodynamics in Gaussian-averaged Lorenz gauge involves (via this example):

1. the Dirac field modelling the electron, with Feynman propagator called the electron propagator (this def.), here to be denoted

   $$\Delta \phantom{AAAA} \text{electron propagator}$$

2. the electromagnetic field modelling the photon, with Feynman propagator called the photon propagator (this prop.), here to be denoted

   $$G \phantom{AAAA} \text{photon propagator}$$

3. the electron-photon interaction

   $$L_{int} \;=\; \underset{ \text{interaction} }{ \underbrace{ i g (\gamma^\mu)^\alpha{}_\beta } } \, \underset{ { \text{incoming} \atop \text{electron} } \atop \text{field} }{\underbrace{\overline{\psi_\alpha}}} \; \underset{ { \, \atop \text{photon} } \atop \text{field} }{\underbrace{a_\mu}} \; \underset{ {\text{outgoing} \atop \text{electron} } \atop \text{field} }{\underbrace{\psi^\beta}}$$

The Feynman diagram for the electron-photon interaction alone is

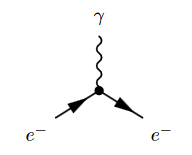
where the solid lines correspond to the electron, and the wiggly line to the photon. The corresponding product of distributions is (written in generalized function-notation)

$$\underset{ \text{loop order} }{ \underbrace{ \hbar^{3/2-1} } } \underset{ \text{electron-photon} \atop \text{interaction} }{ \underbrace{ i g (\gamma^\mu)^\alpha{}_\beta } } \,. \, \underset{ {\text{incoming} \atop \text{electron}} \atop \text{propagator} }{ \underbrace{ \overline{\Delta(-,x)}_{-, \alpha} } } \underset{ { \, \atop \text{photon} } \atop \text{propagator} }{ \underbrace{ G(x,-)_{\mu,-} } } \underset{ { \text{outgoing} \atop \text{electron} } \atop \text{propagator} }{ \underbrace{ \Delta(x,-)^{\beta, -} } }$$

Hence a typical Feynman diagram in the QED Feynman perturbation series induced by this electron-photon interaction looks as follows:

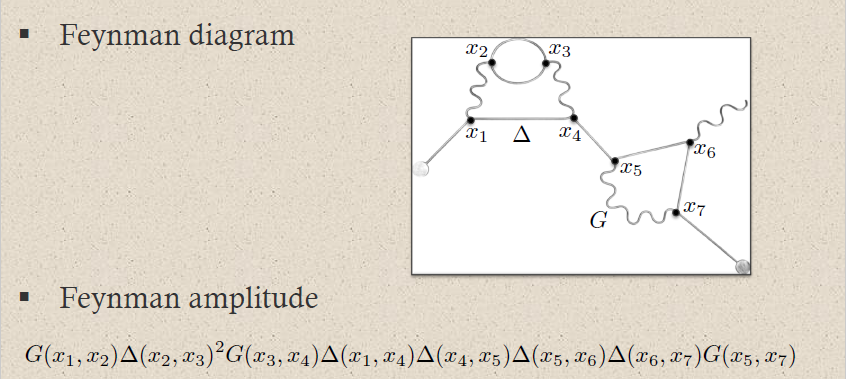
where on the bottom the corresponding Feynman amplitude product of distributions is shown; now notationally suppressing the contraction of the internal indices and all prefactors.

For instance the two solid edges between the vertices $x_2$ and $x_3$ correspond to the two factors of $\Delta(x_2,x_2)$:

This way each sub-graph encodes its corresponding subset of factors in the Feynman amplitude:

graphics grabbed from Brouder 10

A priori this product of distributions is defined away from coincident vertices: $x_i \neq x_j$. The definition at coincident vertices $x_i = x_j$ requires a choice of extension of distributions to the diagonal locus. This choice is the ("re-")normalization of the Feynman amplitude.

Definition

For details see

• at Feynman propagator this def.

• at S-matrix this def.

Related concepts

• photon propagator

References

• Radovan Dermisek, Quantum Electrodynamics (QED) (pdf, pdf)