nLab string scattering amplitude
Context
String theory
Ingredients
Critical string models
Extended objects
Topological strings
Backgrounds
Phenomenology
Quantum field theory
Super-Geometry
superalgebra and (synthetic ) supergeometry
Background
Introductions
Superalgebra
Supergeometry
Supersymmetry
Supersymmetric field theory
Applications
Contents
Idea
In perturbative string theory scattering amplitudes are defined as in quantum field theory, but with n-point functions of 1-dimensional worldline theories (Feynman diagrams) replaced by those of worldsheet 2d CFTs.
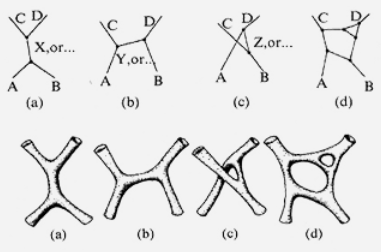
graphics grabbed from Penrose 04, per Jurke 10
Properties
Finiteness
The amplitudes are thought (see the commented references below) to come out term-wise (for each “loop order” hence for each genus and number of punctures of (super-)Riemann surfaces) finite (at least UV-finite), hence renormalized: the higher string oscillations may be seen as providing canonical counterterms for the massless excitations in the effective field theory. In this sense string theory provides a UV-completion of these effective field theories (supergravity coupled to Yang-Mills theory).
Remark
The full perturbation series is the sum of all these (finite) contributions over the genera of Riemann surfaces (the “loop orders”). This sum diverges, even if all loop orders are finite. Notice though, that a non-trivial perturbative QFT is not supposed to have a finite radius of convergence of its scattering amplitudes, since that would imply convergence also for negative coupling constant, which is physically unreasonable. (For the bosonic string the perturbation series has apparently been explicitly shown not to be Borel resummable.) For more on this see at non-perturbative effect and string theory FAQ – Is the divergence of the pertubation series fatal?.
Remark
A string scattering amplitude is called UV-finite at a given loop order (genus of a Riemann surface with marked points/string insertions) if the correlation function is finite for every single such Riemann surface. The actual string amplitude at order though is the averaging of this over all possible conformal structures on , hence the integration of the correlation function, as a function on the conformal structure, over the compactified moduli space of conformal structures (a Deligne-Mumford stack).
If also this integral is finite, hence if the total measure on the moduli space of conformal structures is finite, then one says the amplitude is IR-finite.
This distinction between UV-finiteness and IR-finiteness is not always highlighted in all of the articles below. All authors argue that the string is UV-finite to all order. The IR-finiteness is only discussed much more recently at low loop order.
IR non-finiteness is not physically fatal. For instance if a perturbative theory of quantum gravity develops a cosmological constant perturbatively, then the perturbation series will be IR-divergent, signifying the fact that background spacetime without cosmological constant is no longer a solution to the quantum-corrected equations of motion. Nevertheless, these potential IR-divergences seem to be absent for the superstring perturbation series. For the cosmological constant case this can already be seen from the fact that the effective QFT of type II supergravity etc. does not admit a cosmological constant, for that would violate supersymmetry.
Open-closed scattering duality and KLT relations
The open/closed string duality implies certain relations in string scattering amplitudes that in the point-particle limit induces relations between scattering amplitudes in Yang-Mills theory and in gravity. These are the KLT relations in QFT. See in particular Mafra-Schlotterer 18a, Mafra-Schlotterer 18b, Mafra-Schlotterer 18c.
Twistor string amplitudes and MHV amplitudes in Yang-Mills theory
The scattering amplitudes in twistor string theory induce the MHV amplitudes in (super-)Yang-Mills theory. See at string theory results applied elsewhere in the section Application to QCD – Scattering amplitudes.
-Adic formulation
The Veneziano amplitude (open bosonic string tree-level scattering) has an equivalent formulation as the inverse product over all prime numbers of an amplitude computed not by an integral in the real but in the p-adic numbers. For other open string amplitudes this holds up to some regularization. This is the topic of p-adic string theory, see there for more details.
Examples
Related entries
References
General
A comprehensive account of the superstring S-matrix may be obtained from combining the general idea presented in
- Joseph Polchinski, section 12.5 of vol 2 of String theory, Cambridge Monographs on Mathematical Physics (2001)
with the technical details laid out in
-
Edward Witten, Superstring Perturbation Theory Revisited (arXiv:1209.5461)
-
Edward Witten, More On Superstring Perturbation Theory: An Overview Of Superstring Perturbation Theory Via Super Riemann Surfaces (arXiv:1304.2832)
Survey of the tree level string scattering amplitudes includes
-
Ralph Blumenhagen, Dieter Lüst, Stefan Theisen, String Scattering Amplitudes and Low Energy Effective Field Theory, chapter 16 in Basic Concepts of String Theory Part of the series Theoretical and Mathematical Physics pp 585-639 Springer 2013 (TOC pdf, publisher page)
-
Katrin Becker, Melanie Becker, Ilarion V. Melnikov, Daniel Robbins, Andrew B. Royston, Some tree-level string amplitudes in the NSR formalism, JHEP 12 (2015) 010 (arXiv:1507.02172)
See also
-
Gregory Moore, Symmetries of the Bosonic String S-Matrix (arXiv:hep-th/9310026)
-
Gaston Giribet, Nicholas Labranche, Joan La Madrid, Comments on the two-point string amplitudes [arXiv:2303.15658]
-
Nima Arkani-Hamed, Carolina Figueiredo, Grant N. Remmen: Open String Amplitudes: Singularities, Asymptotics, and New Representations [arXiv:2412.20639]
-
Carolina Figueiredo, Marcos Skowronek: Cuts and Contours [arXiv:2506.05456]
On string scattering amplitudes in view of the S-matrix bootstrap:
- Andrea Guerrieri, Joao Penedones, Pedro Vieira, Where is String Theory? (arXiv:2102.02847)
See also:
- Clifford Cheung, Grant N. Remmen, Francesco Sciotti, Michele Tarquini: Strings from Almost Nothing [arXiv:2508.09246]
For more references see also at string theory results applied elsewhere.
Superstring scattering
A review of superstring scattering amplitudes is in the last section of (Staessens-Vernocke 10). A general discussion of the problem of superstring amplitudes is in
-
Eric D'Hoker, Duong Phong: Loop amplitudes for the fermionic string, Nucl. Phys. B 278 (1986) 225;
-
Greg Moore, P. Nelson, Joseph Polchinski, Strings and supermoduli, Phys. Lett. B 169 (1986) 47-53.
On analycity of the superstring S-matrix:
- Corinne de Lacroix, Harold Erbin, Ashoke Sen, Analyticity and Crossing Symmetry of Superstring Loop Amplitudes (arXiv:1810.07197)
Survey of the presence and role of divergences:
- Ashoke Sen, Ultraviolet and Infrared Divergences in Superstring Theory (arXiv:1512.00026)
Review of the scattering of massive modes in type IIB string theory:
- Nicholas Agia, Massive Type IIB Superstrings Part I: 3- and 4-Point Amplitudes [arXiv:2309.11538]
See also:
- Sergio Luigi Cacciatori, Samuel Grushevsky, Alexander A. Voronov, Tree-Level Superstring Amplitudes: The Neveu-Schwarz Sector [arXiv:2403.09600]
Discussion of superstring scattering amplitudes in terms of pure spinors (Berkovits superstring) with emphasis on KLT relations:
-
Carlos Mafra, Oliver Schlotterer, Towards the -point one-loop superstring amplitude I: Pure spinors and superfield kinematics (arXiv:1812.10969)
-
Carlos Mafra, Oliver Schlotterer, Towards the -point one-loop superstring amplitude II: Worldsheet functions and their duality to kinematics (arXiv:1812.10970)
-
Carlos Mafra, Oliver Schlotterer, Towards the -point one-loop superstring amplitude III: One-loop correlators and their double-copy structure (arXiv:1812.10971)
-
Carlos R. Mafra, Oliver Schlotterer, Tree-level amplitudes from the pure spinor superstring [arXiv:2210.14241]
For more see also at superstring field theory, such as
- Corinne de Lacroix, Harold Erbin, Sitender Pratap Kashyap, Ashoke Sen, Mritunjay Verma, Closed Superstring Field Theory and its Applications, International Journal of Modern Physics AVol. 32, No. 28n29, 1730021 (2017) (arXiv:1703.06410)
The 1-loop amplitudes in type II string theory have been discussed in
- Michael Green, John Schwarz, Supersymmetrical string theories, Phys. Lett. 109 B (1982) 444-448.
and for heterotic string theory in
- David Gross, J.A. Harvey, E.J. Martinec and R. Rohm, Heterotic String Theory (II). The interacting heterotic string, Nucl. Phys. B267 (1986) 75.
The description of 2-loop amplitudes, including the Berezin integral over the super-moduli space of super Riemann surfaces in superstring theory:
-
Eric D'Hoker, Duong Phong, Two-Loop Superstrings I, Main Formulas, Phys. Lett. B529:241-255, 2002 (arXiv:hep-th/0110247)
-
Eric D'Hoker, Duong Phong, Two-Loop Superstrings II, The Chiral Measure on Moduli Space, Nucl. Phys. B636:3-60, 2002 (arXiv:hep-th/0110283)
-
Eric D'Hoker, Duong Phong, Two-Loop Superstrings III, Slice Independence and Absence of Ambiguities, Nucl. Phys. B636:61-79, 2002 (arXiv:hep-th/0111016)
-
Eric D'Hoker, Duong Phong, Two-Loop Superstrings IV, The Cosmological Constant and Modular Forms, Nucl. Phys. B639:129-181, 2002 (arXiv:hep-th/0111040)
-
Eric D'Hoker, Duong Phong, Two-Loop Superstrings V: Gauge Slice Independence of the N-Point Function, Nucl. Phys. B715:91-119, 2005 (arXiv:hep-th/0501196)
-
Eric D'Hoker, Duong Phong, Two-Loop Superstrings VI: Non-Renormalization Theorems and the 4-Point Function, Nucl. Phys. B715:3-90, 2005 (arXiv:hep-th/0501197)
-
Eric D'Hoker, Duong Phong, Two-Loop Superstrings VII, Cohomology of Chiral Amplitudes, Nucl. Phys. B804:421-506, 2008 (arXiv:0711.4314)
Review of this work:
- A.Morozov, NSR Superstring Measures Revisited, JHEP0805:086,2008 (arXiv:0804.3167)
Further developments:
-
Eric D'Hoker, Carlos Mafra, Boris Pioline, Oliver Schlotterer, Two-loop superstring five-point amplitudes I: Construction via chiral splitting and pure spinors (arXiv:2006.05270)
-
Eric D'Hoker, Carlos Mafra, Boris Pioline, Oliver Schlotterer, Two-loop superstring five-point amplitudes II: Low energy expansion and S-duality (doi:2008.08687)
The technical issue of the moduli space of super Riemann surfaces of higher genus (for higher loop string scattering amplitudes) is discussed in
-
Edward Witten, Notes On Super Riemann Surfaces And Their Moduli (arXiv:1209.2459)
-
Ron Donagi, Edward Witten, Supermoduli Space Is Not Projected (arXiv:1304.7798)
On the case of 3-loop:
- Petr Dunin-Barkowski, Igor Fedorov, Alexey Sleptsov: RNS superstring measure for genus 3 [arXiv:2505.02950]
Higher order corrections
- Christopher Pope, Higher-order corrrections in String and M-theory and Generalized Holonomies, December 2006 (pdf)
On finiteness
Here is a commented list of references on the degreewise finiteness of string scattering amplitudes.
Finiteness of bosonic string scattering
Introductory lecture notes:
- Wieland Staessens, Bert Vercnocke, Lectures on Scattering Amplitudes in String Theory, Lecture notes based on lectures given at the fifth Modave School on Mathematical Physics (August 2009) (arXiv:1011.0456)
Discussion of the term-wise finiteness of the bosonic string scattering amplitudes is in
- L. Clavelli, S. T. Jones, Finiteness of the bosonic string in fewer than 26 dimensions, Phys. Rev. D 39, 3795–3797 (1989) (SPIRE)
There are also arguments in
- Simon Davis, On the domain of string perturbation theory, Classical and Quantum Gravity, Volume 6, Issue 12, pp. 1791-1803 (1989) (web)
Finiteness of superstring scattering
Finiteness of heterotic and type II superstring -point functions in flat spacetime is argued for in
- Joseph Atick, Gregory Moore, Ashoke Sen, Catoptrick tadpoles, Nucl.Phys. B307 (1988) 221 (spire)
General finiteness of superstring amplitudes is discussed in
- Stanley Mandelstam, The Loop String Amplitude: Explicit Formulas, Finiteness and Absence of Ambiguities, Phys. Lett. B277 (1992) 82. (inspire)
which shows that a certain divergence which could appear does not.
Also
- A. Restuccia, J. Taylor, Finiteness of type II superstring amplitudes, Physics Letters B, Volume 187, Issues 3–4, 26 March 1987, Pages 267–272
argues finiteness of the superstring amplitudes at each order.
Also:
-
Eric D'Hoker, Duong Phong, Momentum Analyticity and Finiteness of the 1-Loop Superstring Amplitude, Phys. Rev. Lett. 70 (1993) 3692-3695 (arXiv:hep-th/9302003)
-
Eric D'Hoker, Duong Phong, The Box Graph In Superstring Theory, Nucl.Phys.B440:24-94,1995 (arXiv:hep-th/9410152)
-
Eric D'Hoker, Duong Phong, Dispersion Relations in String Theory; Nucl.Phys.B440:24-94,1995 (arXiv:hep-th/9404128)
Arguments for the finiteness of superstring scattering amplitudes to all loop order based on the Berkovits superstring-formulation have been promoted in
- Nathan Berkovits, Multiloop Amplitudes and Vanishing Theorems using the Pure Spinor Formalism for the Superstring, JHEP 0409:047,2004 (arXiv:hep-th/0406055)
(In footnote 2 this article claims that the claimed proofs of the same statement by G.S Danilov in hep-th/9801013, hep-th/0312177 are not in fact proofs.)
Discussion of 2-loop amplitudes from holomorphy arguments:
- Edward Witten, Notes On Holomorphic String And Superstring Theory Measures Of Low Genus (arXiv:1306.3621)
See also:
- Ashoke Sen, Supersymmetry Restoration in Superstring Perturbation Theory (arXiv:1508.02481)
Graviton scattering
Computation of graviton scattering amplitudes (perturbative quantum gravity):
-
Taejin Lee, Gravitational Scattering Amplitudes and Closed String Field Theory in the Proper-Time Gauge, EPJ Web of Conferences 168, 07004 (2018) (doi:10.1051/epjconf/201816807004)
-
Taejin Lee, Four-Graviton Scattering and String Path Integral in the Proper-time gauge (arXiv:1806.02702)
Via AdS/CFT
Discussion via AdS/CFT beyond the SCFT planar limit, using the conformal bootstrap:
- Luis Alday, Agnese Bissi, Eric Perlmutter, Genus-One String Amplitudes from Conformal Field Theory, JHEP06(2019) 010 (arXiv:1809.10670)
More
On point-particle limit via tropical geometry
- Piotr Tourkine, Tropical Amplitudes (arXiv:1309.3551)
Scattering amplitudes of highly excited strings:
- Dimitri P. Skliros, Edmund J. Copeland, Paul M. Saffin, Highly Excited Strings I: Generating Function (arxiv:1611.06498)
Last revised on August 17, 2025 at 11:31:11. See the history of this page for a list of all contributions to it.