nLab Gromoll-Meyer sphere
Context
Differential geometry
synthetic differential geometry
Introductions
from point-set topology to differentiable manifolds
geometry of physics: coordinate systems, smooth spaces, manifolds, smooth homotopy types, supergeometry
Differentials
Tangency
The magic algebraic facts
Theorems
Axiomatics
Models
differential equations, variational calculus
Chern-Weil theory, ∞-Chern-Weil theory
Cartan geometry (super, higher)
Contents
Idea
What is called the Gromoll-Meyer sphere (Gromoll-Meyer 74) is an example of an exotic 7-sphere. It arises as a double coset space/biquotient of the quaternionic unitary group Sp(2) Spin(5) by two copies of Sp(1) SU(2).
Definition
Consider the quaternion unitary group Sp(2) Spin(5) and its two subgroup inclusion of Sp(1) SU(2) as
Then the double coset space/biquotient with respect to the left and right multiplication action, respectively, of these two subgroups is, with respect to its canonically induced geometric structures:
-
homeomorphic to the topological 7-sphere;
-
diffeomorphic to an exotic 7-sphere.
As such, it is called the Gromoll-Meyer sphere, due to Gromoll-Meyer 74
Properties
-
The Gromoll-Meyer sphere is the only exotic 7-sphere that can be modeled by a biquotient of a compact Lie group (KZ02, Corollary C).
-
The Gromoll-Meyer sphere is a 3-sphere-bundle over the 4-sphere.
-
It is a generator of the group of diffeomorphism classes of oriented homotopy spheres in dimension 7, which is of order 28.
Related concepts
coset space-structures on n-spheres:
| standard: | |
|---|---|
| this Prop. | |
| this Prop. | |
| this Prop. | |
| exceptional: | |
| Spin(7)/G₂ is the 7-sphere | |
| since Spin(6) SU(4) | |
| since Sp(2) is Spin(5) and Sp(1) is SU(2), see Spin(5)/SU(2) is the 7-sphere | |
| G₂/SU(3) is the 6-sphere | |
| Spin(9)/Spin(7) is the 15-sphere |
see also Spin(8)-subgroups and reductions
homotopy fibers of homotopy pullbacks of classifying spaces:
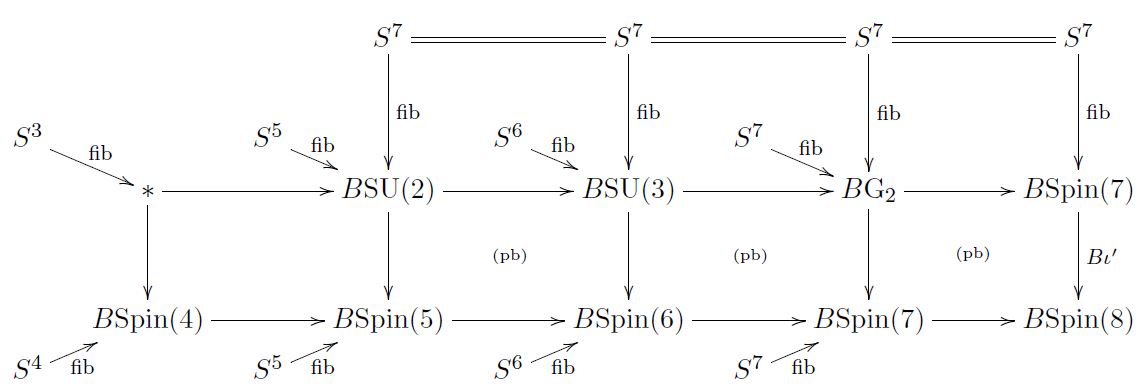
(from FSS 19, 3.4)
References
The construction is due to
- Detlef Gromoll, Wolfgang Meyer, An Exotic Sphere With Nonnegative Sectional Curvature, Annals of Mathematics Second Series, Vol. 100, No. 2 (Sep., 1974), pp. 401-406 (jstor:1971078)
Review includes
- Michael Joachim, D. J. Wraith, pages 7-8 of Exotic spheres and curvature (pdf)
Generalization of the construction to a large class of exotic 7-spheres:
- C. Duran, T. Puettmann, A. Rigas, An infinite family of Gromoll-Meyer spheres. Arch. Math. (2010) 95: 269 (arXiv:math/0610349, doi:10.1007/s00013-010-0161-x)
See also:
-
Jost-Hinrich Eschenburg, Martin Kerin, Almost positive curvature on the Gromoll-Meyer sphere, Proc. Amer. Math. Soc (arXiv:0711.2987)
-
Carlos Durán, Thomas Püttmann, A minimal Brieskorn 5-sphere in the Gromoll-Meyer sphere and its applications, Michigan Math. J. Volume 56, Issue 2 (2008), 419-451 (euclid)
-
Llohann D. Sperança, Pulling back the Gromoll-Meyer construction and models of exotic spheres, Proceedings of the American Mathematical Society 144.7 (2016): 3181-3196 (arXiv:1010.6039)
-
Llohann D. Sperança, Explicit Constructions over the Exotic 8-sphere (pdf, pdf)
-
David S. Berman, Martin Cederwall, Tancredi Schettini Gherardini: Curvature of an exotic 7-sphere [arXiv:2410.01909]
For a proof that the Gromoll-Meyer sphere is the only exotic sphere that is a biquotient of a compact Lie group see
- Vitali Kapovitch, Wolfgang Ziller, Biquotients with singly generated rational cohomology, (arXiv:math/0210231)
Last revised on October 4, 2024 at 05:28:33. See the history of this page for a list of all contributions to it.