nLab Spin(7)
Context
Group Theory
- group, ∞-group
- group object, group object in an (∞,1)-category
- abelian group, spectrum
- super abelian group
- group action, ∞-action
- representation, ∞-representation
- progroup
- homogeneous space
Classical groups
Finite groups
Group schemes
Topological groups
Lie groups
Super-Lie groups
Higher groups
Cohomology and Extensions
Related concepts
Contents
Idea
The spin group in dimension .
Properties
Subgroups and Supgroups
Proposition
(Spin(7)-subgroups in Spin(8))
There are precisely 3 conjugacy classes of Spin(7)-subgroups inside Spin(8), and the triality group acts transitively on these three classes.
(Varadarajan 01, Theorem 5 on p. 6)
Proposition
(G₂ is intersection of Spin(7)-subgroups of Spin(8))
The intersection inside Spin(8) of any two Spin(7)-subgroups from distinct conjugacy classes of subgroups (according to Prop. ) is the exceptional Lie group G₂, hence we have pullback squares of the form
(Varadarajan 01, Theorem 5 on p. 13)
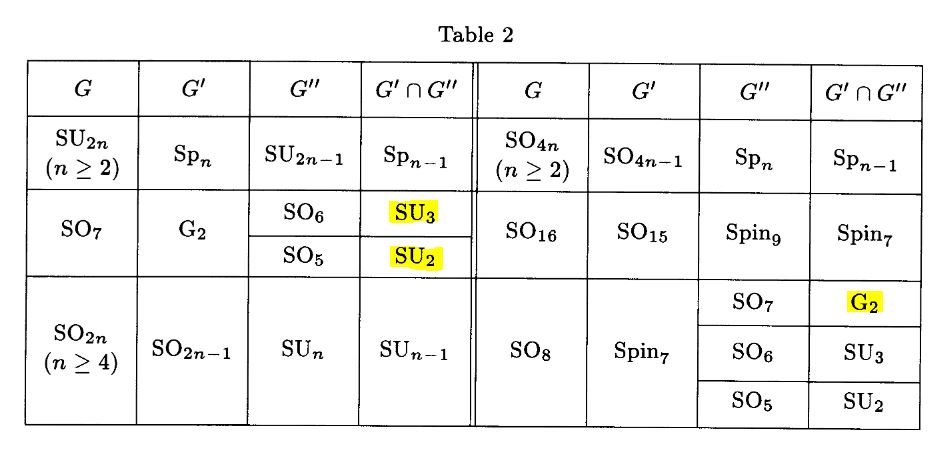
Proposition
We have the following commuting diagram of subgroup inclusions, where each square exhibits a pullback/fiber product, hence an intersection of subgroups:
Here in the bottom row we have the Lie groups
Spin(5) Spin(6) Spin(7) Spin(8)
with their canonical subgroup-inclusions, while in the top row we have
and the right vertical inclusion is the one of the two non-standard inclusions, according to Prop. .
Proof
The square on the right is that from Prop. .
The square in the middle is Varadarajan 01, Lemma 9 on p. 10.
The statement also follows with Onishchik 93, Table 2, p. 144:
Coset spaces
Proposition
(coset space of Spin(7) by G₂ is 7-sphere)
Consider the canonical action of Spin(7) on the unit sphere in (the 7-sphere),
-
This action is is transitive;
-
the stabilizer group of any point on is G₂;
-
all G₂-subgroups of Spin(7) arise this way, and are all conjugate to each other.
Hence the coset space of Spin(7) by G₂ is the 7-sphere
(e.g Varadarajan 01, Theorem 3)
coset space-structures on n-spheres:
| standard: | |
|---|---|
| this Prop. | |
| this Prop. | |
| this Prop. | |
| exceptional: | |
| Spin(7)/G₂ is the 7-sphere | |
| since Spin(6) SU(4) | |
| since Sp(2) is Spin(5) and Sp(1) is SU(2), see Spin(5)/SU(2) is the 7-sphere | |
| G₂/SU(3) is the 6-sphere | |
| Spin(9)/Spin(7) is the 15-sphere |
see also Spin(8)-subgroups and reductions
homotopy fibers of homotopy pullbacks of classifying spaces:
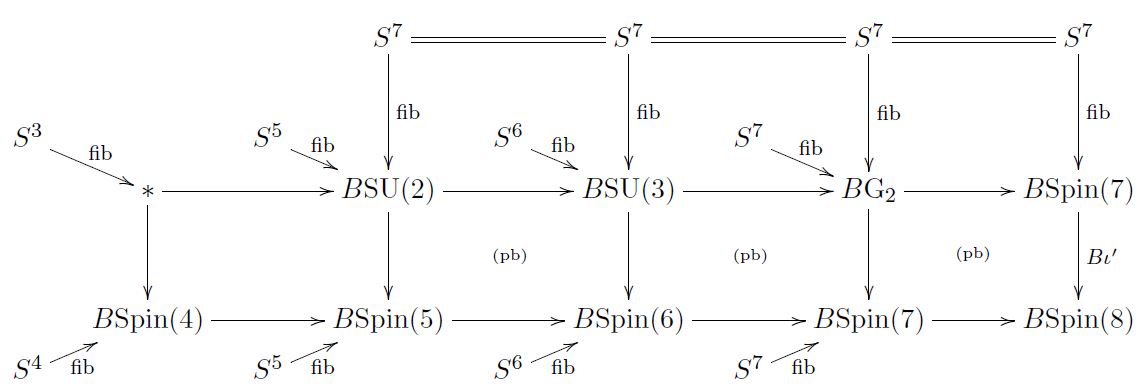
(from FSS 19, 3.4)
-Structure and exceptional geometry
Spin(8)-subgroups and reductions to exceptional geometry
see also: coset space structure on n-spheres
Related concepts
rotation groups in low dimensions:
see also
classification of special holonomy manifolds by Berger's theorem:
References
-
A. L. Onishchik (ed.) Lie Groups and Lie Algebras
-
I. A. L. Onishchik, E. B. Vinberg, Foundations of Lie Theory,
-
II. V. V. Gorbatsevich, A. L. Onishchik, Lie Transformation Groups
Encyclopaedia of Mathematical Sciences, Volume 20, Springer 1993
-
-
Veeravalli Varadarajan, Spin(7)-subgroups of SO(8) and Spin(8), Expositiones Mathematicae Volume 19, Issue 2, 2001, Pages 163-177 (doi:10.1016/S0723-0869(01)80027-X, pdf)
Last revised on July 18, 2024 at 11:23:46. See the history of this page for a list of all contributions to it.