nLab all horizontal weight systems are partitioned Lie algebra weight systems
Context
Knot theory
Examples/classes:
Types
Related concepts:
Lie theory
∞-Lie theory (higher geometry)
Background
Smooth structure
Higher groupoids
Lie theory
∞-Lie groupoids
∞-Lie algebroids
Formal Lie groupoids
Cohomology
Homotopy
Related topics
Examples
-Lie groupoids
-Lie groups
-Lie algebroids
-Lie algebras
Contents
Idea
All weight systems on horizontal chord diagrams may be realized as linear combinations of Lie algebra weight systems applied not necessarily to the given horizontal chord diagram itself, but to the result of regarding each of its strands as resolved by some finite number of strands.
We state this precisely as Prop. below (due to Bar-Natan 96). First we introduce all the definitions that enter the statement:
Ingredients
Given any ground field (or in fact just any commutative ground ring)
1) write for the linear span of horizontal chord diagrams modulo the 2T relations and the 4T relations
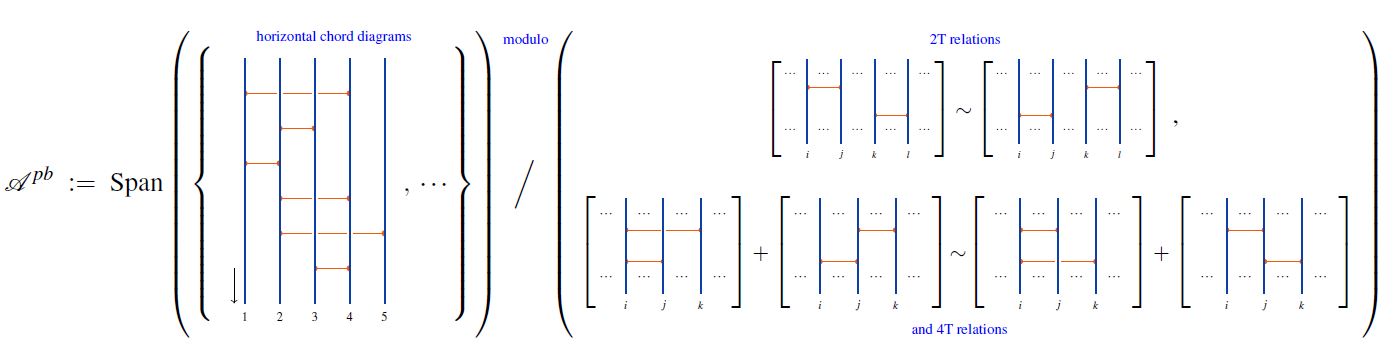
graphics from Sati-Schreiber 19c
regarded as a graded vector space, graded by the number of chords,
and write
for its degreewise dual vector space: the space of horizontal weight systems;
2) write
for projection onto and inclusion of the linear subspace spanned by horizontal chord diagrams with strands;
3) write
for the operation that reads in a finite tuple of natural numbers, with sum , and produces the linear map
which takes a horizontal chord diagram with strands to the linear combination of chord diagrams obtained by replacing its -th strand by strands for all and then summing over all ways of re-attaching chords, with any vertex previously on some strand now to be put on one of the strands (Bar-Natan 96, Def. 2.2).
For example:
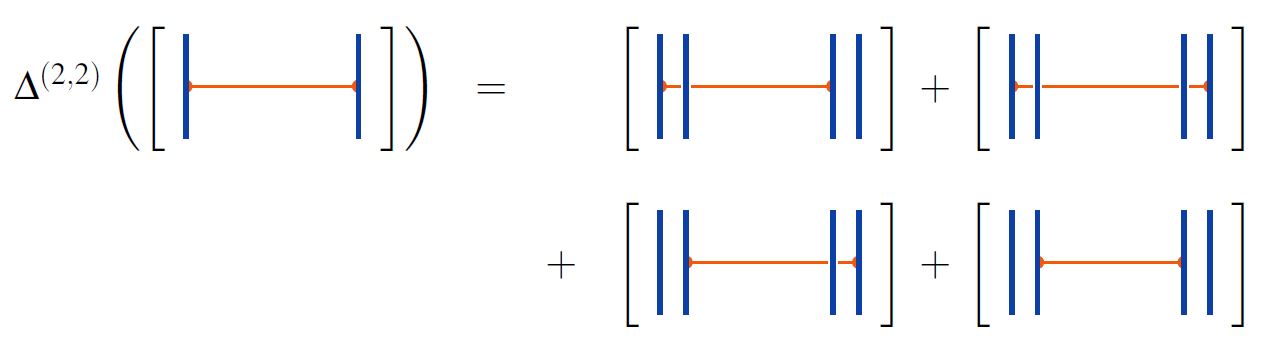
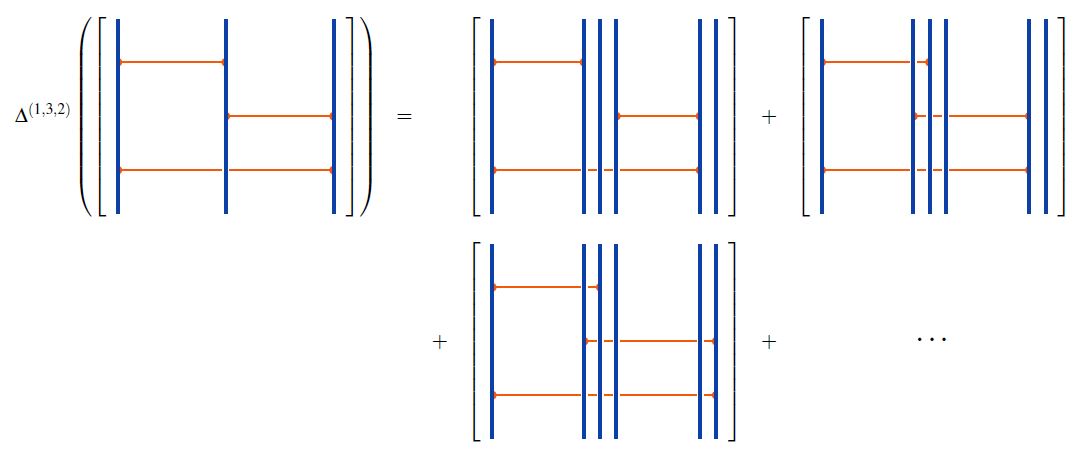
graphics from Sati-Schreiber 19c
Moreover, for a metric Lie algebra
1) write
for its set of isomorphism classes of finite dimensional Lie algebra representations (Lie modules)
2) write
for the function that sends a Lie module over to the corresponding endomorphism ring-valued Lie algebra weight system on horizontal chord diagrams.
Finally, for
-
a Lie algebra representation of ,
-
a permutation of elements
write
for the composite operation of
-
composing an endomorphism on the -fold tensor power of by the braiding according to the permutation ;
-
forming the trace of the resulting endomorphism of .
Then the composition of
-
the partitioning function (2);
-
the assignment (3) of Lie algebra weight systems;
yields a function from triples consisting of a Lie module, a tuple of natural numbers and a permutation to horizontal weight systems:
Finally, write also
for the linear extension of this function (5) to the linear span of its domain set.
Statement
Proposition
(all horizontal weight systems are partitioned Lie algebra weight systems)
For consider the general linear Lie algebra , regarded as a metric Lie algebra not via its Killing form, but via the fundamental trace .
Then the space (1) of weight systems on horizontal chord diagrams is spanned by partitioned -Lie algebra weight systems, in that the linear extension (6) of the function (5) assigning -Lie algebra weight systems composed with partitioning (2) is an epimorphism:
This is the statement of Bar-Natan 96, Corollary 2.6.
For example:
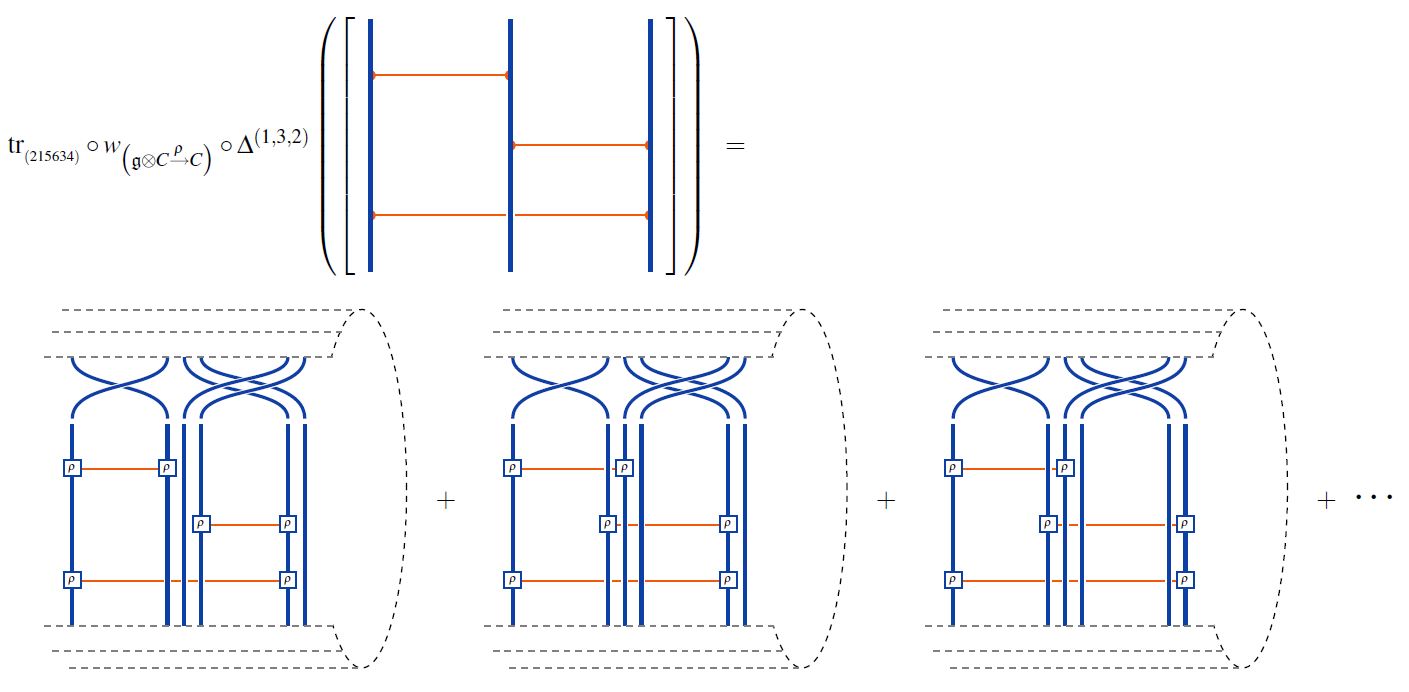
graphics from Sati-Schreiber 19c
Applications
Chord diagrams as multi-trace observables in the BMN matrix model
The supersymmetric states of the BMN matrix model are temporally constant complex matrices which are complex metric Lie representations of su(2) (interpreted as fuzzy 2-sphere noncommutative geometries of giant gravitons or equivalently as fuzzy funnels of D0-D2 brane bound states).
A fuzzy 2-sphere-rotation invariant multi-trace observable on these supersymmetric states is hence an expression of the following form:
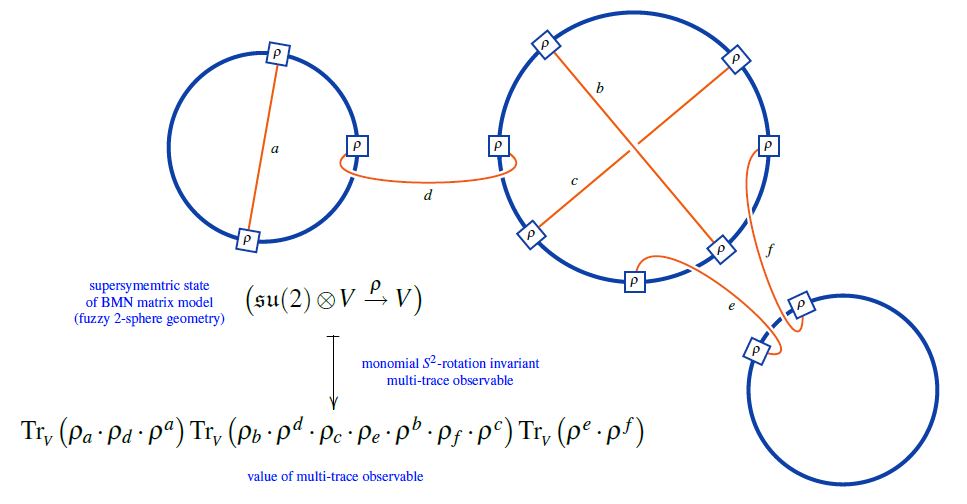
(from Sati-Schreiber 19c)
Here we are showing the corresponding string diagram/Penrose notation for metric Lie representations, which makes manifest that
-
these multi-trace observables are encoded by Sullivan chord diagrams
-
their value on the supersymmetric states is the evaluation of the corresponding Lie algebra weight system on .
Or equivalently, if is a horizontal chord diagram whose -permuted closure is (see here) then the values of the invariant multi-trace observables on the supersymmetric states of the BMN matrix model are the evaluation of on , as shown here:
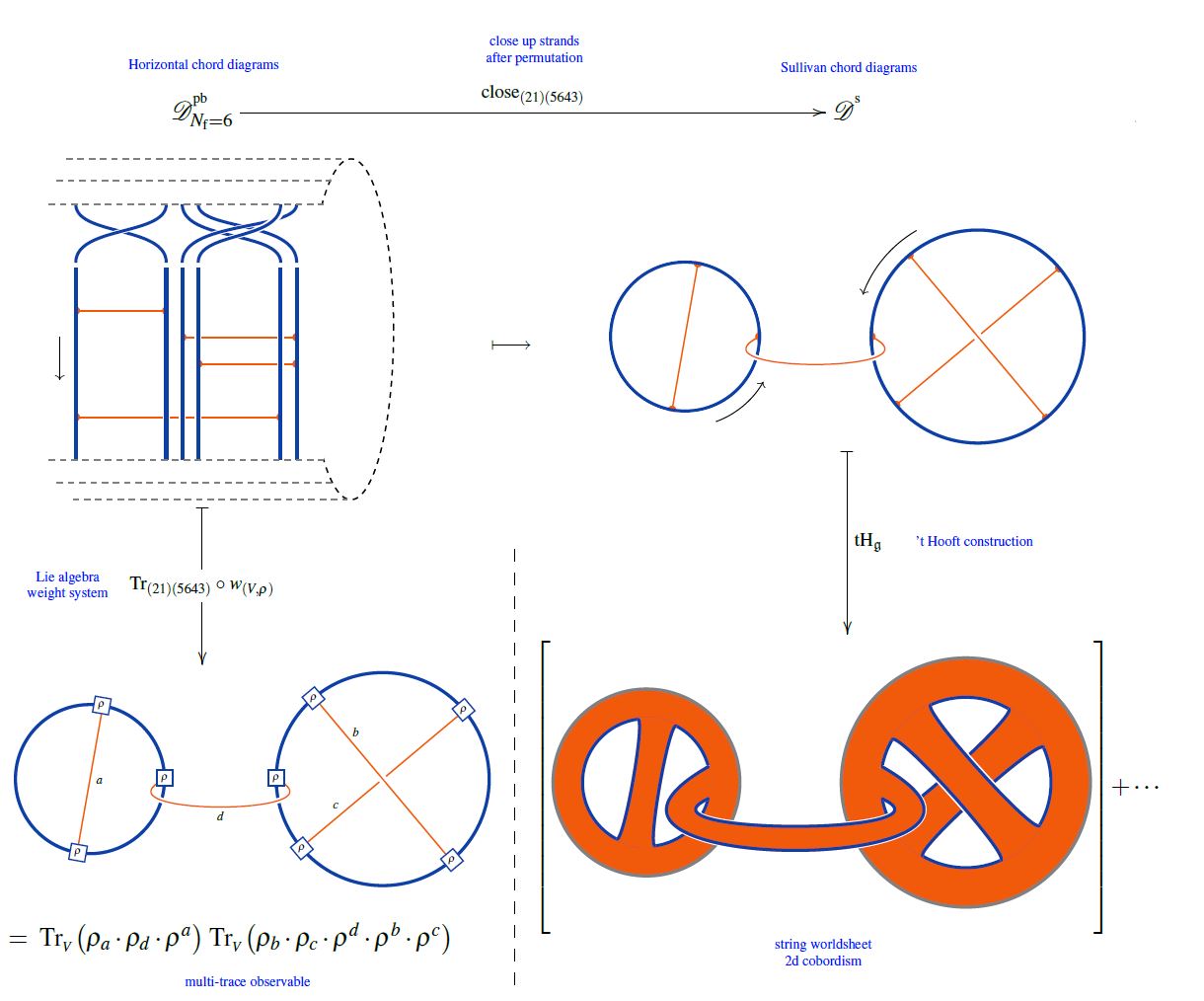
(from Sati-Schreiber 19c)
But since all horizontal weight systems are partitioned Lie algebra weight systems this way, this identifies supersymmetric states of the BMN matrix model as seen by invariant multi-trace observables as horizontal chord diagrams evaluated in Lie algebra weight systems.
Related theorems
Facts about chord diagrams and their weight systems:
References
The theorem and its proof is due to:
- Dror Bar-Natan, Vassiliev and Quantum Invariants of Braids, Geom. Topol. Monogr. 4 (2002) 143-160 (arxiv:q-alg/9607001)
Last revised on December 7, 2021 at 16:00:54. See the history of this page for a list of all contributions to it.