nLab
M9-brane

Idea

The $\mathbb{Z}_2$-orbifold/higher orientifold fixed point in Hořava-Witten theory might be called it O9-plane but is often called the M9-brane (e.g. GKSTY 02, section 3, Moore-Peradze-Saulina 04), even though it is on a different conceptual footing than the genuine M2-brane and M5-brane.

In (Hull 97, pages 8-9) the M9-brane was argued to be the object whose charge is the Poincaré dual to the time-component of the M2-brane charge as it appears in the M-theory super Lie algebra via

$$\wedge^2 (\mathbb{R}^{10,1})^\ast \simeq \wedge^2 (\mathbb{R}^{10})^\ast \oplus \wedge^{9} \mathbb{R}^{10} \,.$$

(In the same way the time component of the M5-brane charge is argued to be dual to the charge of the KK-monopole, see there.)

Under the duality between M-theory and type IIA string theory the M9-brane may be identified with the O8-plane:

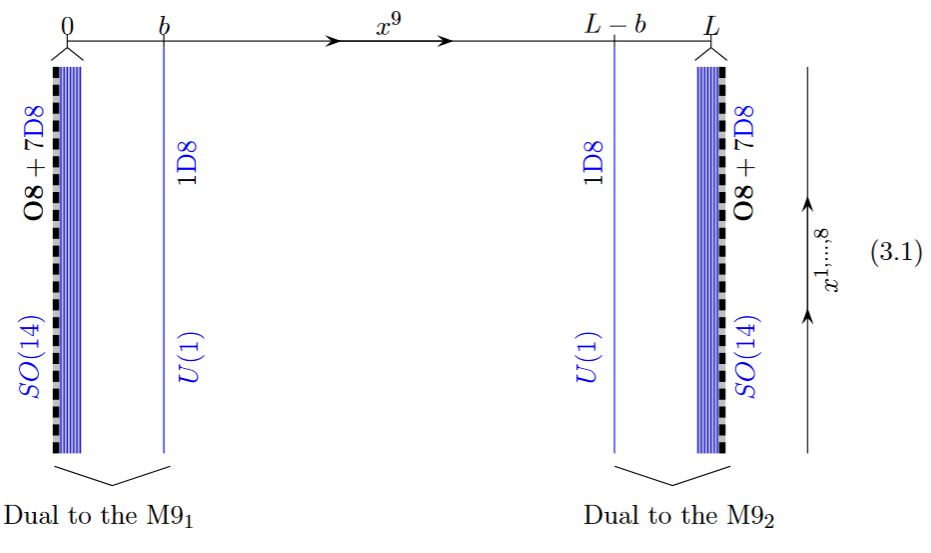
from GKSTY 02, section 3

This may be used to understand the gauge enhancement to E8-gauge groups at the heterotic boundary of Horava-Witten theory:

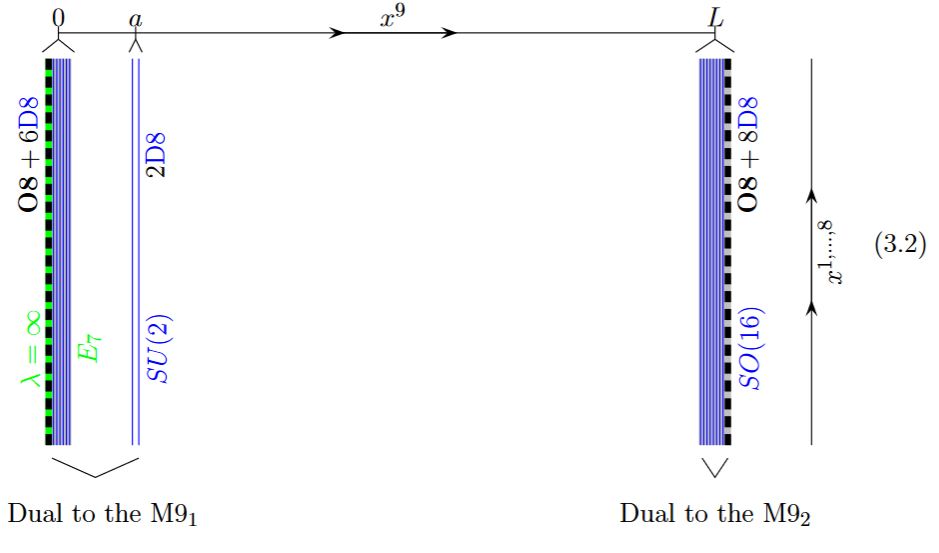
from GKSTY 02, section 3

Related concepts

• ninebrane group, ninebrane structure

• KK monopole

Table of branes appearing in supergravity/string theory (for classification see at brane scan).

brane	in supergravity	charged under gauge field	has worldvolume theory
black brane	supergravity	higher gauge field	SCFT
D-brane	type II	RR-field	super Yang-Mills theory
$(D = 2n)$	type IIA	$\,$	$\,$
D0-brane	$\,$	$\,$	BFSS matrix model
D2-brane	$\,$	$\,$	$\,$
D4-brane	$\,$	$\,$	D=5 super Yang-Mills theory with Khovanov homology observables
D6-brane	$\,$	$\,$	D=7 super Yang-Mills theory
D8-brane	$\,$	$\,$
$(D = 2n+1)$	type IIB	$\,$	$\,$
D(-1)-brane	$\,$	$\,$	$\,$
D1-brane	$\,$	$\,$	2d CFT with BH entropy
D3-brane	$\,$	$\,$	N=4 D=4 super Yang-Mills theory
D5-brane	$\,$	$\,$	$\,$
D7-brane	$\,$	$\,$	$\,$
D9-brane	$\,$	$\,$	$\,$
(p,q)-string	$\,$	$\,$	$\,$
(D25-brane)	(bosonic string theory)
NS-brane	type I, II, heterotic	circle n-connection	$\,$
string	$\,$	B2-field	2d SCFT
NS5-brane	$\,$	B6-field	little string theory
D-brane for topological string			$\,$
A-brane			$\,$
B-brane			$\,$
M-brane	11D SuGra/M-theory	circle n-connection	$\,$
M2-brane	$\,$	C3-field	ABJM theory, BLG model
M5-brane	$\,$	C6-field	6d (2,0)-superconformal QFT
M9-brane/O9-plane			heterotic string theory
M-wave
topological M2-brane	topological M-theory	C3-field on G2-manifold
topological M5-brane	$\,$	C6-field on G2-manifold
solitons on M5-brane	6d (2,0)-superconformal QFT
self-dual string		self-dual B-field
3-brane in 6d

References

Discussion of a possible black 9-brane in 11d is in

• Chris Hull, Gravitational Duality, Branes and Charges, Nucl. Phys. B509 (1998) 216-251 (arXiv:hep-th/9705162)

The term “M9-brane” maybe originates in

• Eric Bergshoeff, Jan Pieter van der Schaar, On M-9-branes (arXiv:hep-th/9806069)

A proposal for a description of the M9 as an higher WZW theory is in

• Takeshi Sato, A 10-form Gauge Potential and an M-9-brane Wess-Zumino Action in Massive 11D Theory, Phys. Lett. B477 (2000) 457-468 (arXiv:hep-th/9912030)

Discussion of how the M2-brane and the M5-brane may arise from this by tachyon condensation is in

• Laurent Houart, Yolanda Lozano, Brane Descent Relations in M-theory, Phys.Lett. B479 (2000) 299-307 (arXiv:hep-th/0001170)

Discussion of the M9 as the dual in Horava-Witten theory of O8-planes in type II string theory is in

• E. Gorbatov, V.S. Kaplunovsky, J. Sonnenschein, Stefan Theisen, S. Yankielowicz, section 3 of On Heterotic Orbifolds, M Theory and Type I’ Brane Engineering, JHEP 0205:015, 2002 (arXiv:hep-th/0108135)

see also at Intersection of D6s with O8s

Cohomological discussion of ninebrane structures is in

• Hisham Sati, Ninebrane structures (arXiv:1405.7686)

See also

• Paul Howe, A. Kaya, Ergin Sezgin, P. Sundell, Codimension One Branes (arXiv:hep-th/0001169)

• Gregory Moore, Grigor Peradze, Natalia Saulina, Instabilities in heterotic M-theory induced by open membrane instantons, Nucl.Phys. B607 (2001) 117-154 (arXiv:hep-th/0012104)

• Takeshi Sato, On M-9-branes and their dimensional reductions, Nucl. Phys. Proc. Suppl. 102 (2001) 107-112 (arXiv:hep-th/0102084)

Discussion of open M5-branes ending on the M9 is in

• Eric Bergshoeff, Gary Gibbons, Paul Townsend, Open M5-branes, Phys. Rev. Lett. 97:231601 2006 (arXiv:hep-th/0607193)