nLab M5-MO9 brane bound state
Context
String theory
Ingredients
Critical string models
Extended objects
Topological strings
Backgrounds
Phenomenology
Contents
Idea
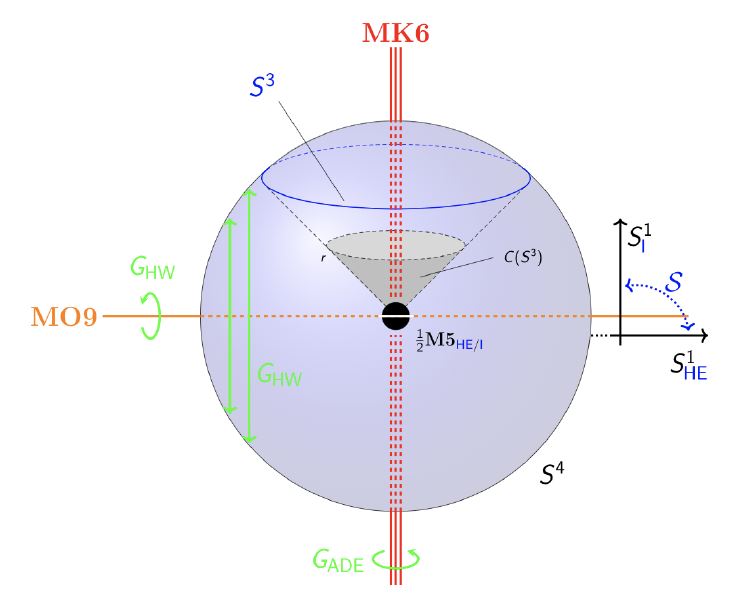
The brane intersection of M5-branes with MO9-planes – the “half M5-brane”.
Equivalently:
-
under duality between M-theory and heterotic string theory: black NS5-brane solitons in heterotic string theory.
-
under duality between M-theory and type IIA string theory:
D4-D8-brane bound states or half NS5-brane in type I' string theory
graphics grabbed from HSS18, Example 2.2.7
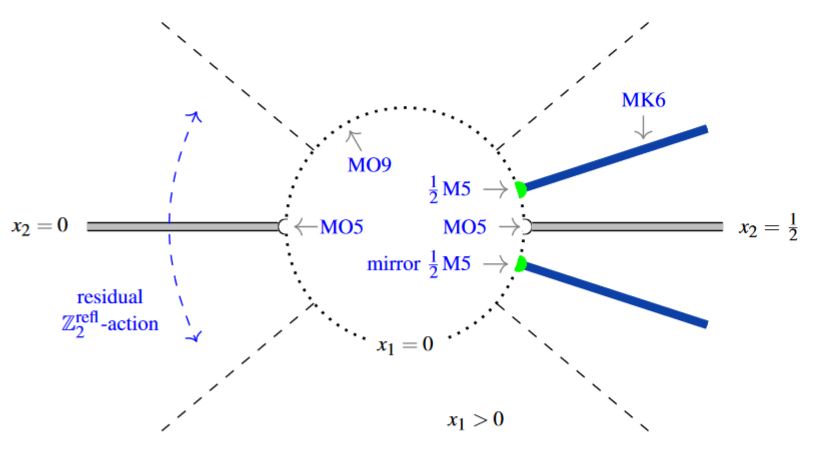
graphics grabbed from SS 19, Section 4
In string theory
As Yang-Mills instantons in heterotic string theory
In (dual) heterotic string theory wrapped NS5-branes are equivalently Yang-Mills instantons in the transversal Yang-Mills theory (Strominger 90, Witten 96, p. 10) – as is generally the case for Dp-D(p+4)-brane bound states (see there).
As half NS5-branes in type I’
(For more see at half NS5-brane.)
If a black NS5-brane sits at an O8-plane, hence at the orientifold fixed point-locus, then in the ordinary -quotient it appears as a “half-brane” with only one copy of D6-branes ending on it:
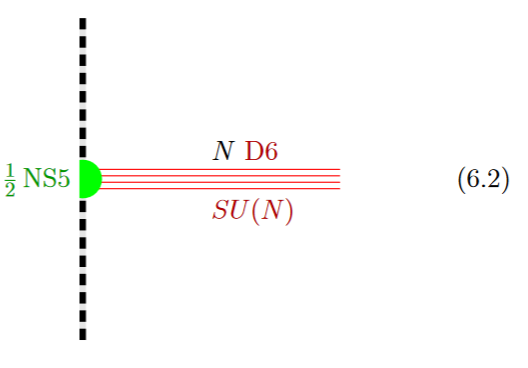
from GKSTY 02
(In Hanany-Zaffaroni 99 this is interpreted in terms of the 't Hooft-Polyakov monopole.)
The lift to M-theory of this situation is an M5-brane intersecting an M9-brane (see at MO5-plane and at heterotic M-theory on ADE-orbifolds):
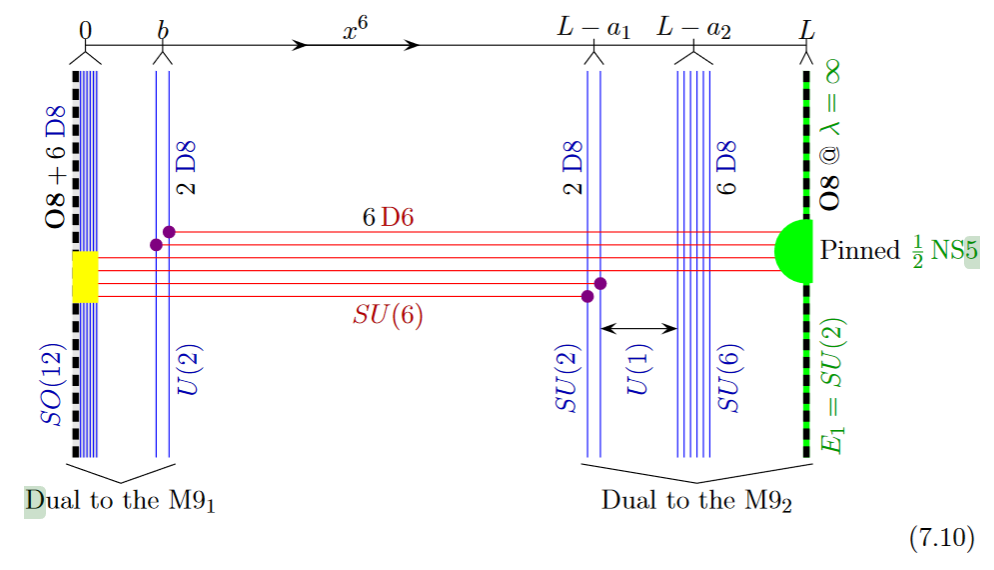
from GKSTY 02
Alternatively the O8-plane may intersect the black D6-branes away from the black NS5-brane:
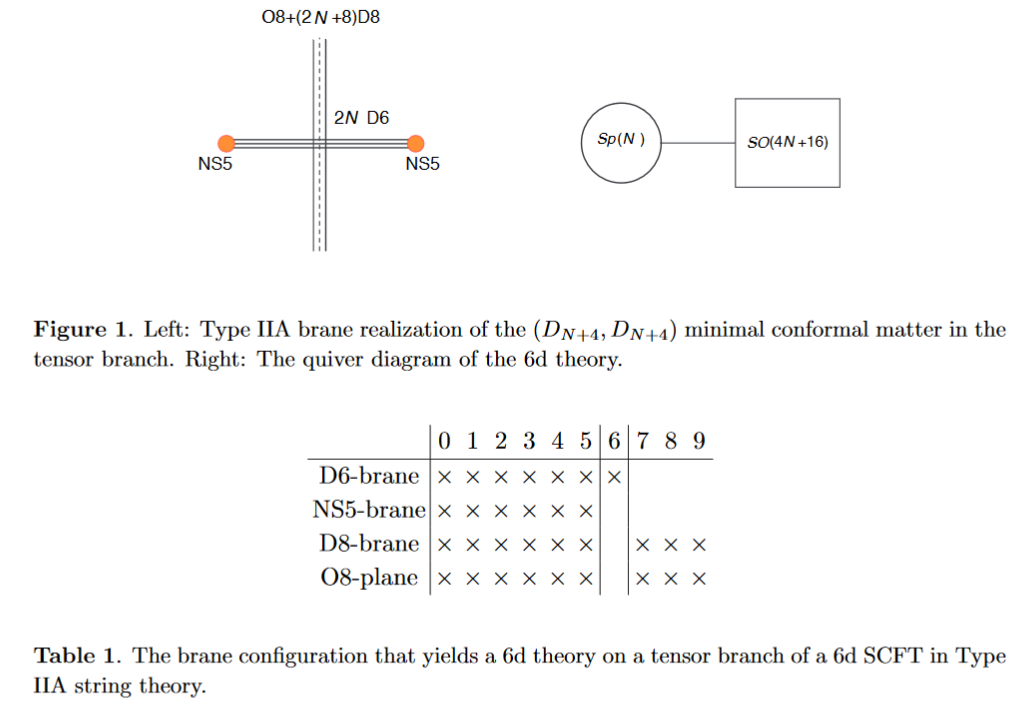
from HKLY 15
In general, some of the NS5 sit away from the O8-plane, while some sit on top of it:
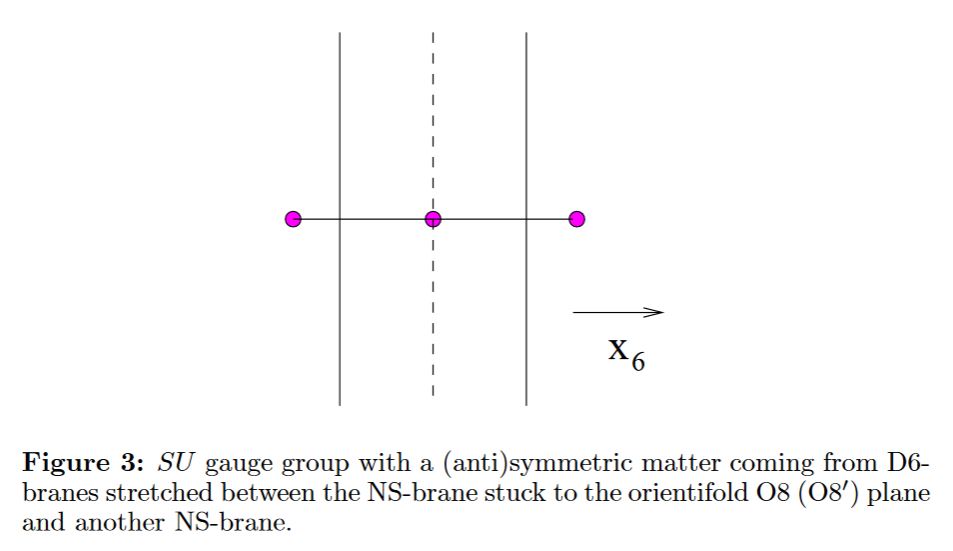
from Hanany-Zaffaroni 98

graphics grabbed from Apruzzi-Fazzi 17, p. 18
Related concepts
brane intersections/bound states/wrapped branes/polarized branes
-
D-branes and anti D-branes form bound states by tachyon condensation, thought to imply the classification of D-brane charge by K-theory
-
intersecting D-branes/fuzzy funnels:
-
Dp-D(p+6) brane bound state
References
As heterotic Yang-Mills instantons
Discussion as Yang-Mills instantons (“small instantons”):
-
Andrew Strominger, Heterotic solitons, Nucl. Phys. B343 (1990) 167-184 (doi:10.1016/0550-3213(90)90599-9) Erratum: Nucl. Phys. B353 (1991) 565-565 (doi:10.1016/0550-3213(91)90349-3) (spire:27900)
-
Edward Witten, Small Instantons in String Theory, Nucl.Phys.B460:541-559, 1996 (doi:10.1016/0550-3213(95)00625-7)
As half M5-branes
-
Fabio Apruzzi, Marco Fazzi, Section 2.1.2 of: AdS7/CFT6 with orientifolds, JHEP 01 (2018) 124 (arXiv:1712.03235)
-
John Huerta, Hisham Sati, Urs Schreiber, Example 2.2.7 of: Real ADE-equivariant (co)homotopy and Super M-branes, CMP (2019) (arXiv:1805.05987, doi:10.1007/s00220-019-03442-3)
-
Domenico Fiorenza, Hisham Sati, Urs Schreiber, Section 4 of: Super-exceptional geometry: origin of heterotic M-theory and super-exceptional embedding construction of M5 (arXiv:1908.00042)
-
Hisham Sati, Urs Schreiber, Section 4.1 of: Equivariant Cohomotopy implies orientifold tadpole cancellation (arXiv:1909.12277)
Last revised on November 27, 2021 at 12:59:54. See the history of this page for a list of all contributions to it.