nLab third stable homotopy group of spheres
Context
Stable Homotopy theory
Ingredients
Contents
Cobordism theory
cobordism theory = manifolds and cobordisms + stable homotopy theory/higher category theory
Concepts of cobordism theory
-
homotopy classes of maps to Thom space MO
-
complex cobordism cohomology theory
flavors of bordism homology theories/cobordism cohomology theories, their representing Thom spectra and cobordism rings:
bordism theoryM(B,f) (B-bordism):
relative bordism theories:
global equivariant bordism theory:
algebraic:
Contents
Idea
The third stable homotopy group of spheres (the third stable stem) is the cyclic group of order 24:
where the generator is represented by the quaternionic Hopf fibration .
Properties
As the third framed bordism group
Under the Pontrjagin-Thom isomorphism, identifying the stable homotopy groups of spheres with the bordism ring of stably framed manifolds (see at MFr), the generator (1) is represented by the 3-sphere (with its left-invariant framing induced from the identification with the Lie group SU(2) Sp(1) )
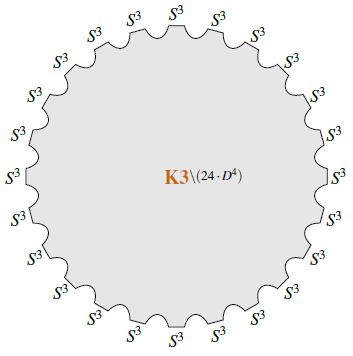
Moreover, the relation is represented by the bordism which is the complement of 24 open balls inside the K3-manifold (e.g. Wang-Xu 10, Sec. 2.6, Bauer 10, SP 17).
Via the fourth -bordism group
Equivalently, the elements of are detected by half the Todd classes of cobounding manifolds with special unitary group-tangential structure on their stable tangent bundle (elements of the MSUFr-bordism ring):
We have the following short exact sequence of the MSU-, MSUFr- and MFr-bordism rings (Conner-Floyd 66, p. 104)
which produces from half the Todd class of cobounding -manifolds the KO-theoretic Adams e-invariant (Adams 66, p. 39) of the boundary manifold in . For this detects the third stable homotopy group of spheres, by the following:
Proposition
(Adams 66, Example 7.17 and p. 46)
In degree 3, the KO-theoretic e-invariant takes the value on the quaternionic Hopf fibration and hence reflects the full third stable homotopy group of spheres:
while sees only “half” of it (by Adams 66, Prop. 7.14).
Related concepts
References
The original computation:
- Vladimir Abramovich Rokhlin, On a mapping of the -dimensional sphere into the -dimensional sphere, (Russian) Doklady Akad. Nauk SSSR (N.S.) 80, (1951). 541–544
with a mistake (in the unstable range) corrected in
- Vladimir Abramovich Rokhlin, New results in the theory of four-dimensional manifolds, (Russian) Doklady Akad. Nauk SSSR (N.S.) 84, (1952). 221–224.
French translations are in:
- Lucien Guillou, Alexis Marin (eds.), A la Recherche de la Topologie Perdue: I. Du côté de chez Rohlin. II. Le côté de Casson, Progress in Mathematics 62, Birkhäuser Boston 1985 (ISBN:0817633294, 9780817633295)
Review:
- Guozhen Wang, Zhouli Xu, Section 2.6 of: A survey of computations of homotopy groups of Spheres and Cobordisms, 2010 (pdf)
See also:
- Mehmet Kirdar, On the First, the Second and the Third Stems of the Stable Homotopy Groups of Spheres [arXiv:2107.06103]
More on the computation via the framed cobordism ring and the K3-manifold giving the cobordism that witnesses the order of 24:
-
Tilman Bauer, answer to: third stable homotopy group of spheres via geometry?, 2010 (MO:a/44885)
-
Chris Schommer-Pries, answer to: Nilpotence of the stable Hopf map via framed cobordism, 2017 (MO:a/218053)
Via immersions of 3-spheres into Euclidean 4-space
-
A. Szűcs, Two Theorems of Rokhlin, Journal of Mathematical Sciences 113, 888–892 (2003) (doi:10.1023/A:1021208007146)
-
Tobias Ekholm, Masamichi Takase, Singular Seifert surfaces and Smale invariants for a family of 3-sphere immersions, Bulletin of the London Mathematical Society 43 (2011) 251–266 (arXiv:0903.0238)
Discussion of geometric string bordism in degreee 3 as a means to speak (via the Pontryagin-Thom theorem) about the third stable homotopy group of spheres:
-
Domenico Fiorenza, Eugenio Landi, Integrals detecting degree 3 string cobordism classes [arXiv:2209.12933]
-
Domenico Fiorenza, String bordism invariants in dimension 3 from -valued TQFTs, talk at QFT and Cobordism, CQTS (Mar 2023) [web]
Last revised on June 23, 2023 at 10:39:28. See the history of this page for a list of all contributions to it.