nLab topological membrane
Context
String theory
Ingredients
Critical string models
Extended objects
Topological strings
Backgrounds
Phenomenology
Contents
Idea
A membrane sigma-model topological quantum field theory that is roughly related to topological M-theory as the M2-brane is related to M-theory and to the topological string (A-model/B-model) as the M2-brane is related to the string and to the topological M5-brane as the M2-brane is related to the M5-brane.
The target space of the topological membrane is a G₂-manifold, the action functional is governed by the higher holonomy of the compatible supergravity C-field over the membrane worldvolume.
Definition
According to (Bao-Bengtsson-Cederwall-Nillson 05, equation (2.14)) the topological -brane is the super 2-brane which exists in according to the brane scan, which says that the super Poincare Lie algebra in carries an exceptional Lie algebra cocycle of degree , hence admits the Green-Schwarz action functional for a super 2-brane.
Related concepts
The brane scan.
The Green-Schwarz type super -brane sigma-models (see at table of branes for further links and see at The brane bouquet for the full classification):
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 11 | M2 | M5 | ||||||||
| 10 | D0 | F1, D1 | D2 | D3 | D4 | NS5, D5 | D6 | D7 | D8 | D9 |
| 9 | * | |||||||||
| 8 | * | |||||||||
| 7 | M2 | |||||||||
| 6 | F1, S1 | S3 | ||||||||
| 5 | * | |||||||||
| 4 | * | * | ||||||||
| 3 | * |
(The first columns follow the exceptional spinors table.)
The corresponding exceptional super L-∞ algebra cocycles (schematically, without prefactors):
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 11 | on sIso(10,1) | on m2brane | ||||||||
| 10 | on sIso(9,1) | on StringIIA | on StringIIB | on StringIIA | on sIso(9,1) | on StringIIA | on StringIIB | in StringIIA | on StringIIB | |
| 9 | on sIso(8,1) | |||||||||
| 8 | on sIso(7,1) | |||||||||
| 7 | on sIso(6,1) | |||||||||
| 6 | on sIso(5,1) | on sIso(5,1) | ||||||||
| 5 | on sIso(4,1) | |||||||||
| 4 | on sIso(3,1) | on sIso(3,1) | ||||||||
| 3 | on sIso(2,1) |
The Brane molecule
Furthermore, there exists a more general classification of possible supermembranes in spacetime with spatial dimensions and time dimensions, appearing in (Blencowe-Duff 88). In this sense, the brane scan is but the branch of the brane molecule. The objects appearing here are expected to be related to other generalizations of string theory. See D=12 supergravity and bosonic M-theory.
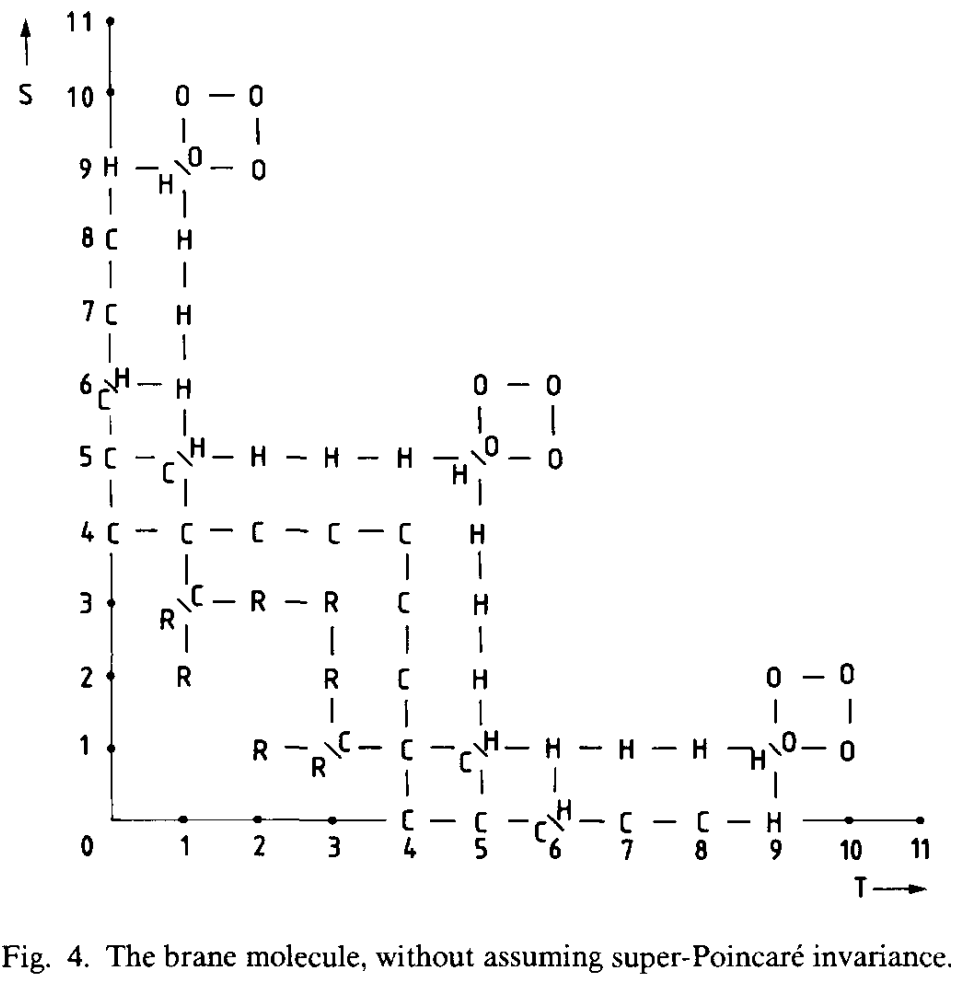
Compare:
-
Miles Blencowe, Mike Duff, Supermembranes and the Signature of Space-time, Nucl. Phys. B310 (1988) 387-404 (spire:262142, 10.1016/0550-3213(88)90155-1, pdf)
Table of branes appearing in supergravity/string theory (for classification see at brane scan).
References
- Ling Bao, Viktor Bengtsson, Martin Cederwall, Bengt Nilsson, Membranes for Topological M-Theory (arXiv:hep-th/0507077)
-
Giulio Bonelli, Alessandro Tanzini, Maxim Zabzine, On topological M-theory (arXiv:hep-th/0509175)
-
Ling Bao, Topological membranes, Nucl. Phys. Proc. Suppl. 171 (2007) 259-260 (inspire)
In the context of exceptional generalized geometry:
- Noriaki Ikeda, Tatsuya Tokunaga, Topological Membranes with 3-Form H Flux on Generalized Geometries, Adv.Theor.Math.Phys.12:1259-1281,2008 (arXiv:hep-th/0609098)
Last revised on July 18, 2024 at 13:06:17. See the history of this page for a list of all contributions to it.