nLab enhanced gauge symmetry
Context
Physics
physics, mathematical physics, philosophy of physics
Surveys, textbooks and lecture notes
theory (physics), model (physics)
experiment, measurement, computable physics
-
-
-
Axiomatizations
-
Tools
-
Structural phenomena
-
Types of quantum field thories
-
Chern-Weil theory
Ingredients
Connection
Curvature
Theorems
Contents
Idea
Generally, an enhanced gauge symmetry refers to the appearance of gauge theory with a larger gauge group than may be superficially apparent.
On coincident D-branes
A famous case is the enhanced gauge symmetry in the Chan-Paton gauge fields of coincident D-branes. A priori each D-brane carries a complex line bundle/circle principal bundle, but as of them coincide the gauge group is expected to enhance from to the unitary group (or the special unitary group ).
Mathematically this gauge enhancement on D-branes is modeled by the Baum-Douglas geometric cycle model for K-homology (Reis-Szabo 05, def. 1.5 and p. 16, Szabo 08, p. 4): One such cycle is given by a submanifold of spacetime equipped with spin^c structure and with a complex vector bundle , and given two such cycles and with the same underlying manifold (“coincident D-brane worldvolume”) then their formal direct sum is identified with the single cycle carrying the direct sum of vector bundles
If here has rank and hence structure group , then the direct sum of vector bundles has structure group the product group .
In particular the sum of coincident cycles each carrying a line bundle yields a rank- vector bundle with structure group . In this sense then a cycle carrying a general rank -vector bundle, hence with structure group , may be thought of as a “gauge enhancement” of making D-branes coincide.
From massless BPS states
In the context of the realization of super Yang-Mills theories as effective field theories of superstring theory, BPS branes in the string background becomes BPS states of the SYM theory. These become massless as the cycles on which the BPS charge is supported shrink away (at boundary points of the given moduli space). In this case these additional massless states may appear as additional gauge bosons in the compactified gauge theory which thereby develops a larger gauge group. Typically a previously abelian gauge group becomes non-abelian this way.
Examples include KK-compactification of M-theory on K3 fibers and on G₂-manifolds with ADE singularities, corresponding to F-theory on elliptic fibrations making K3-fibrations with singular fibers, corresponding to heterotic string theory on singular elliptic fibrations. See at
-
M-theory on G₂-manifolds the section Nonabelian gauge groups and chiral fermions at orbifold singularities;
-
F-theory the section F-brane scan
For MK6 branes at ADE-singularities
The blow-up of an ADE-singularity is given by a union of Riemann spheres that touch each other such as to form the shape of the Dynkin diagram whose A-D-E label corresponds to that of the given finite subgroup of SU(2).
This statement is originally due to (duVal 1934 I, p. 1-3 (453-455)). A description in terms of hyper-Kähler geometry is due to Kronheimer 89a.
Quick survey of this fact is in Reid 87, a textbook account is Slodowy 80.
In string theory this fact is interpreted in terms of gauge enhancement of the M-theory-lift of coincident black D6-branes to an MK6 at an ADE-singularity (Sen 97):
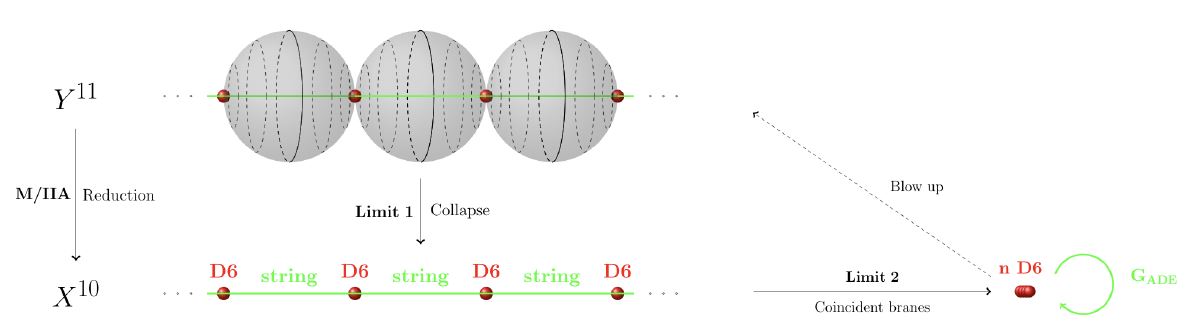
graphics grabbed from HSS18
See at M-theory lift of gauge enhancement on D6-branes for more.
On M9-Branes
In Horava-Witten theory there is supposed to be gauge enhancement over the M9-branes such as to identify their worldvolume theory with E8-heterotic string theory.
Under the duality between M-theory and type IIA string theory the M9-brane may be identified with the O8-plane:
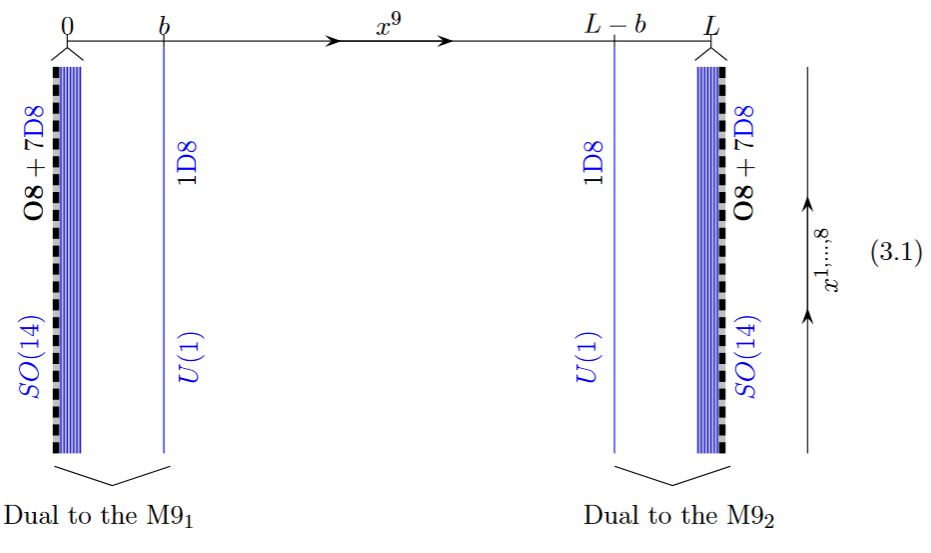
from GKSTY 02, section 3
This may be used to understand the gauge enhancement to E8-gauge groups at the heterotic boundary of Horava-Witten theory:
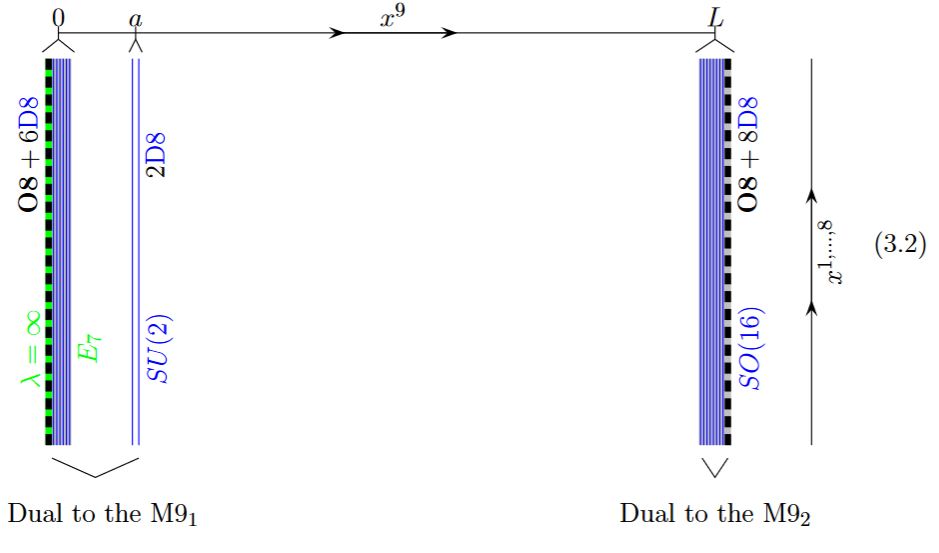
from GKSTY 02, section 3
Related concepts
References
On coincident D-branes
The idea that on coincident D-branes there is gauge enhancement to -gauge field theory is due to
- Edward Witten, section 3 of: Bound States Of Strings And -Branes, Nucl. Phys. B 460 (1996) 335-350 [doi:10.1016/0550-3213(95)00610-9, arXiv:hep-th/9510135]
There, this is an “obvious guess” (first line on p. 8).
Subsequently, most authors cite this obvious guess as a fact; for instance the review:
- Robert Myers, section 3 of: Nonabelian Phenomena on D-branes, Class. Quant. Grav. 20 (2003) [arXiv:hep-th/0303072, doi:10.1088/0264-9381/20/12/302]
Discussion in terms of boundary conformal field theory is in
- Jürgen Fuchs, P. Kaste, Wolfgang Lerche, C. Lutken, Christoph Schweigert, J. Walcher, Boundary Fixed Points, Enhanced Gauge Symmetry and Singular Bundles on K3, Nucl.Phys.B598:57-72, 2001 (arXiv:hep-th/0007145)
By actual computation in open string field theory “convincing evidence” for the nonabelian Yang-Mills theory on coincident D-branes was found, numerically, in (see bottom of p. 22)
- Erasmo Coletti, Ilya Sigalov, Washington Taylor, Abelian and nonabelian vector field effective actions from string field theory, JHEP 0309 (2003) 050 (arXiv:hep-th/0306041)
Similar numerical derivation, as well as exact derivation at zero momentum, is in
- Nathan Berkovits, Martin Schnabl: Yang-Mills Action from Open Superstring Field Theory, JHEP 0309 (2003) 022 [arXiv:hep-th/0307019, doi:10.1088/1126-6708/2003/09/022]
The first full derivation seems to be claimed by:
- Taejin Lee: Covariant open bosonic string field theory on multiple D-branes in the proper-time gauge, Journal of the Korean Physical Society 71 12 (2017) 886–903 [arXiv:1609.01473, doi:10.3938/jkps.71.886]
surveyed in
- Taejin Lee, Deformation of the Cubic Open String Field Theory, Phys. Lett. B 768 (2017) 248 [arXiv:1701.06154, doi:10.1016/j.physletb.2017.02.065]
That on D0-branes this reproduces the BFSS matrix model and on D(-1)-branes the IKKT matrix model is shown in
- Taejin Lee, Covariant Open String Field Theory on Multiple D-Branes (arXiv:1703.06402)
Discussion of gauge enhancement on coincident D-branes in terms of Baum-Douglas geometric cycles for K-homology is in
- Rui Reis, Richard Szabo, Geometric K-Homology of Flat D-Branes ,Commun.Math.Phys. 266 (2006) 71-122, Journal of the Korean Physical Society December 2017, Volume 71, Issue 12, pp 886–903 (arXiv:hep-th/0507043)
reviewed in
- Richard Szabo, D-branes and bivariant K-theory, Noncommutative Geometry and Physics 3 1 (2013): 131. (arXiv:0809.3029)
Derivation via rational parameterized stable homotopy theory applied to The brane bouquet is in
- Vincent Braunack-Mayer, Hisham Sati, Urs Schreiber, Gauge enhancement of Super M-Branes, Comm. Math. Phys. 371 (2019) 197-265 [arXiv:1806.01115, doi:10.1007/s00220-019-03441-4]
On M-branes at ADE-singularities
The picture of M-theory lift of gauge enhancement on D6-branes is due to
- Ashoke Sen, Section 2, A Note on Enhanced Gauge Symmetries in M- and String Theory, JHEP 9709:001,1997 (arXiv:hep-th/9707123)
Review of the standard lore of gauge enhancement in M-theory includes
- Adam B. Barrett, section 2.3 (following Acharya-Gukov 04) of M-Theory on Manifolds with Holonomy, 2006 (arXiv:hep-th/0612096)
(…)
General
Original articles include
-
Edward Witten, section 4.6 of String Theory Dynamics In Various Dimensions, Nucl.Phys.B443:85-126,1995 (arXiv:hep-th/9503124)
-
Chris Hull, Paul Townsend, Enhanced Gauge Symmetries in Superstring Theories, Nucl.Phys. B451 (1995) 525-546 (arXiv:hep-th/9505073)
-
Paul Aspinwall, Enhanced Gauge Symmetries and K3 Surfaces, Phys.Lett. B357 (1995) 329-334 (arXiv:hep-th/9507012)
-
Chris Hull, Duality, Enhanced Symmetry and Massless Black Holes, in Proceedings of Strings’95: Future Perspectives in String Theory (World Scientific, 1996, I. Bars et al. eds.), p. 230 (pdf)
-
M. Bershadsky, Ken Intriligator, Shamit Kachru, David Morrison, V. Sadov, Cumrun Vafa, Geometric Singularities and Enhanced Gauge Symmetries, Nucl.Phys.B481:215-252,1996 (arXiv:hep-th/9605200)
-
Philip Candelas, Eugene Perevalov, Govindan Rajesh, Toric Geometry and Enhanced Gauge Symmetry of F-Theory/Heterotic Vacua, Nucl.Phys. B507 (1997) 445-474 (arXiv:hep-th/9704097)
-
Mirjam Cvetic, Chris Hull, Wrapped Branes and Supersymmetry, Nucl.Phys.B519:141-158,1998 (arXiv:hep-th/9709033)
-
Bobby Acharya, Sergei Gukov, M theory and Singularities of Exceptional Holonomy Manifolds, Phys.Rept.392:121-189,2004 (arXiv:hep-th/0409191)
-
James Halverson, David Morrison, On Gauge Enhancement and Singular Limits in Compactifications of M-theory (arXiv:1507.05965)
-
Neil Lambert, Miles Owen, Charged Chiral Fermions from M5-Branes (arXiv:1802.07766)
Discussion via duality of M9-branes to O-planes is in
- E. Gorbatov, V.S. Kaplunovsky, J. Sonnenschein, Stefan Theisen, S. Yankielowicz, section 3 of On Heterotic Orbifolds, M Theory and Type I’ Brane Engineering, JHEP 0205:015, 2002 (arXiv:hep-th/0108135)
Last revised on March 19, 2025 at 14:49:34. See the history of this page for a list of all contributions to it.