nLab M-theory lift of gauge enhancement on D6-branes

Idea

It is well understood that in type IIA string theory there appears

• $SU(N)$ enhanced gauge symmetry on $N$-coincident D-branes;

• $SO(2N)$ enhanced gauge symmetry on $N$-coincident D-branes at an orientifold plane.

The physical picture of this effect is that the gauge bosons of these gauge fields are the modes of the open strings stretching between these D-branes which become massless as the branes coincide.

Now, as the situation is lifted to M-theory, the D0-branes, D2-branes and D4-branes lift to M2-branes and M5-branes, and the gauge enhancement is thought to be similarly reflected on these M-branes (as exhibited for the M2-branes by the BLG-model and ABJM-model).

But for the D6-brane the situation is different: the D6-brane lifts not to an M-brane, but to a configuration of the field of 11-dimensional supergravity: the 11d Kaluza-Klein monopole.

Here we discuss the picture of how gauge enhancement on D6-branes in type IIA string theory is reflected on Kaluza-Klein monopoles at ADE-singularities. The explicit realization reviewed below is due to (Sen 97).

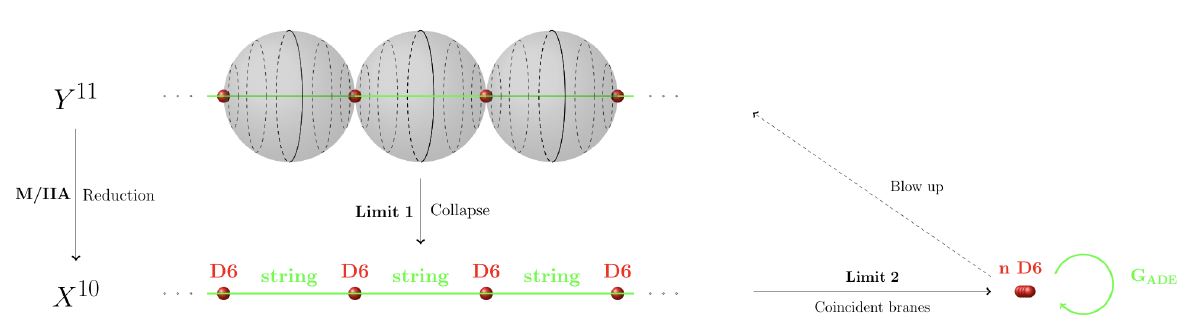
graphics grabbed from HSS18

Construction

$A_{N-1}$-singularity and $SU(N)$-gauge enhancement

The 11d multi-centered Kaluza-Klein monopole spacetime has metric tensor of the form

$$ds^2 \coloneqq - d t^2 + \underoverset{n = 5}{10}{\sum} d y^n d y^n + ds^2_{TN} \,,$$

where

$$ds^2_{TN} \coloneqq V^{-1}( d x^4 + \vec \omega \cdot d \vec r )^2 + V d \vec r^2$$

is the metric tensor of the multi-centered Taub-NUT space, with $x^4$ the canonical coordinate on a circle and with

$$V \coloneqq 1 + \underoverset{I = 1}{N}{\sum} \frac{4m}{{\vert \vec r - \vec r_I\vert}}$$

and

$$\vec \nabla \times \vec \omega = - \vec \nabla V$$

for $\{\vec r_I\}_{I =1}^N$ the set of positions of the KK-monopoles of mass $m$.

Notice that the radius $16 \pi m V^{-1/2}$ of the $x^4$-circle vanishes precisely at the positions $\vec r_I$. Nevertheless, as long as all the $\vec r_I$ are distinct, then the above is a smooth spacetime also at the positions of the $\vec r_I$ – if the periodicity of $x^4$ is taken to be $16 \pi m$. But with this periodicity fixed, then as the $N$ monopole positions $\vec r_I$ coincide, then the resulting metric has a conical singularity at that point, of ADE-singularity type $A_{N-1}$.

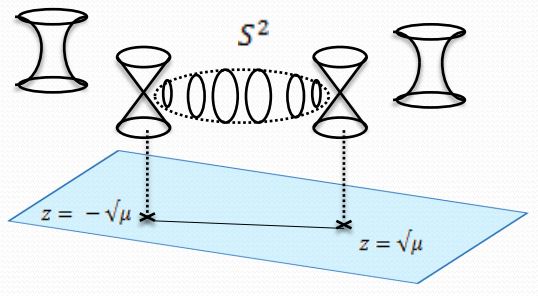
To see where the gauge enhancement arises from in this singular case, observe that in the non-singular configuration there are $N-1$ linearly indepent 2-cycles $S_{i j}$ in the multi-center KK-monopole spacetime, represented by the the 2-spheres that are swept out by the circle fiber as it moves from $\vec r_i$ to $\vec r_j$ (remembering that the circle fiber radius vanishes precisely at the positions $\vec r_I$).

For the canonical choice of straight path between $\vec r_i$ and $\vec r_j$ (and arbitrary fixed position in the remaining 7 dimensions) then the surface area of these 2-spheres is

$$vol(S_{i j}) = 16 \pi m {\vert \vec r_i - \vec r_j\vert} \,.$$

For any other choice of path the surface area will be larger. Hence an M2-brane with tension $T_{M2}$ swrapping the 2-cycle $S_{i j}$ has minimal tension energy when in the configuration of these spheres, namely

$$m_{i j} = 16 \pi m T_{M2} {\vert \vec r_i - \vec r_j\vert} \,.$$

The type IIA limit is given by $m \to 0$. In this limit the M2-branes wrapping the above cycles become the type IIA superstring by double dimensional reduction, the KK-monopoles become the D6-branes, and it is evident from the geometry that the membrane warpping $S_{i j}$ becomes an open string strentching between the $i$th and the $j$th D6-brane.

In the limit $m \to 0$ the D6-branes coincide,the strings stretching between them become massless (in accord with the above formula for the wrapped M2-brane mass), and become the gauge bosons of an $SU(N)$ Chan-Paton gauge field.

(Sen 97, section 2)

$D_{N}$-singularity and $SO(2N)$-gauge enhancement

Now consider the above setupmodified by replacing the Taub-NUT space with coordinates $(\vec r, x^4)$ by its $\mathbb{Z}/2$-orbifold given by the $\mathbb{Z}/2$-action with nontrivial operation given by

$$(\vec r, x^4) \mapsto (- \vec r, - x^4)$$

and in the Taub-NUT metric replace $V$ by

$$V \coloneqq 1 - \frac{16m}{r} + \underoverset{i = 1}{N}{\sum} \left( \frac{4m}{\vert \vec r - \vec r_i\vert} + \frac{4m}{\vert \vec r + \vec r_i\vert} \right) \,.$$

The type IIA image of the origin of this configuration is an orientifold plane.

Now as the $\vec r_i$ all approach 0 we get an 11d spacetime with a $D_N$-type ADE-singularity, whose type IIA image is $N$ D6-branes coincident on an orientifold plane.

(Sen 97, section 3)

Related concepts

• heterotic M-theory on ADE-orbifolds

• membrane triple junction

from M-branes to F-branes: superstrings, D-branes and NS5-branes

M-theory on $S^1_A \times S^1_B$-elliptic fibration	KK-compactification on $S^1_A$	type IIA string theory	T-dual KK-compactification on $S^1_B$	type IIB string theory	geometrize the axio-dilaton	F-theory on elliptically fibered-K3 fibration	duality between F-theory and heterotic string theory	heterotic string theory on elliptic fibration
M2-brane wrapping $S_A^1$	double dimensional reduction $\mapsto$	type IIA superstring	$\mapsto$	type IIB superstring	$\mapsto$	“	$\mapsto$	heterotic superstring
M2-brane wrapping $S_B^1$	$\mapsto$	D2-brane	$\mapsto$	D1-brane	$\mapsto$	“
M2-brane wrapping $p$ times around $S_A^1$ and $q$ times around $S_B^1$	$\mapsto$	$p$ strings and $q$ D2-branes	$\mapsto$	(p,q)-string	$\mapsto$	“
M5-brane wrapping $S_A^1$	double dimensional reduction $\mapsto$	D4-brane	$\mapsto$	D5-brane	$\mapsto$	“
M5-brane wrapping $S_B^1$	$\mapsto$	NS5-brane	$\mapsto$	NS5-brane	$\mapsto$	“	$\mapsto$	NS5-brane
M5-brane wrapping $p$ times around $S_A^1$ and $q$ times around $S_B^1$	$\mapsto$	$p$ D4-brane and $q$ NS5-branes	$\mapsto$	(p,q)5-brane	$\mapsto$	“
M5-brane wrapping $S_A^1 \times S_B^1$	$\mapsto$		$\mapsto$	D3-brane	$\mapsto$	“
KK-monopole/A-type ADE singularity (degeneration locus of $S^1_A$-circle fibration, Sen limit of $S^1_A \times S^1_B$ elliptic fibration)	$\mapsto$	D6-brane	$\mapsto$	D7-branes	$\mapsto$	A-type nodal curve cycle degeneration locus of elliptic fibration (Sen 97, section 2)		SU-gauge enhancement
KK-monopole orientifold/D-type ADE singularity	$\mapsto$	D6-brane with O6-planes	$\mapsto$	D7-branes with O7-planes	$\mapsto$	D-type nodal curve cycle degeneration locus of elliptic fibration (Sen 97, section 3)		SO-gauge enhancement
exceptional ADE-singularity	$\mapsto$		$\mapsto$		$\mapsto$	exceptional ADE-singularity of elliptic fibration	$\mapsto$	E6-, E7-, E8-gauge enhancement

(e.g. Johnson 97, Blumenhagen 10)

Refrences

• Ashoke Sen, A Note on Enhanced Gauge Symmetries in M- and String Theory, JHEP 9709:001,1997 (arXiv:hep-th/9707123)