nLab hadron supersymmetry
Context
Fields and quanta
fields and particles in particle physics
and in the standard model of particle physics:
matter field fermions (spinors, Dirac fields)
| flavors of fundamental fermions in the standard model of particle physics: | |||
|---|---|---|---|
| generation of fermions | 1st generation | 2nd generation | 3d generation |
| quarks () | |||
| up-type | up quark () | charm quark () | top quark () |
| down-type | down quark () | strange quark () | bottom quark () |
| leptons | |||
| charged | electron | muon | tauon |
| neutral | electron neutrino | muon neutrino | tau neutrino |
| bound states: | |||
| mesons | light mesons: pion () ρ-meson () ω-meson () f1-meson a1-meson | strange-mesons: ϕ-meson (), kaon, K*-meson (, ) eta-meson () charmed heavy mesons: D-meson (, , ) J/ψ-meson () | bottom heavy mesons: B-meson () ϒ-meson () |
| baryons | nucleons: proton neutron |
(also: antiparticles)
hadrons (bound states of the above quarks)
minimally extended supersymmetric standard model
bosinos:
dark matter candidates
Exotica
Contents
Idea
Hadron supersymmetry (Miyazawa 66, Miyazawa 68) is an approximate (dynamically broken) supersymmetry among the experimentally observed spectra of hadrons, hence an approximate symmetry of quantum hadrodynamics, relating the masses of mesons (which are bosons) to baryons (which are fermions) and further to tetraquarks (which are again bosons).
This experimentally observed (see below) hadron flavor supersymmetry is in contrast to the more popular but also more speculative idea of color charge supersymmetry (super QCD, MSSM), which hypothesizes that quarks and gluons have superpartners. While these (squarks and gluinos) have not been observed, even single quarks have never been observed, due to their confinement inside hadrons.
A model of confined QCD which brings out the hadron supersymmetry is holographic light front QCD.
In terms of geometric engineering of QFT via intersecting D-brane models, hadron supersymmetry means that the flavor brane is supersymmetric, while the color brane may not be.
Theory
From the constituent quark model of hadrons in quantum chromodynamics, the phenomenon of hadron supersymmetry follows (Catto & Gürsey 1985, 1988) from the fact that
-
both single antiquarks as well as diquarks carry the same color charge ,
-
color charge predominantly determines the properties of bound states in QCD,
-
the exchange of anti-quarks with diquarks inside the bound state with yet another quark exchanges mesons with baryons,
this gives an approximate symmetry of confined QCD as shown on the left here:
Dually, both quarks as well as anti-diquarks carry color charge , which leads to a further such transformation exchanging baryons with tetraquarks, as shown on the right.
These transformations organize into a supersymmetry operation, successively relating mesons, baryons and tetraquarks:
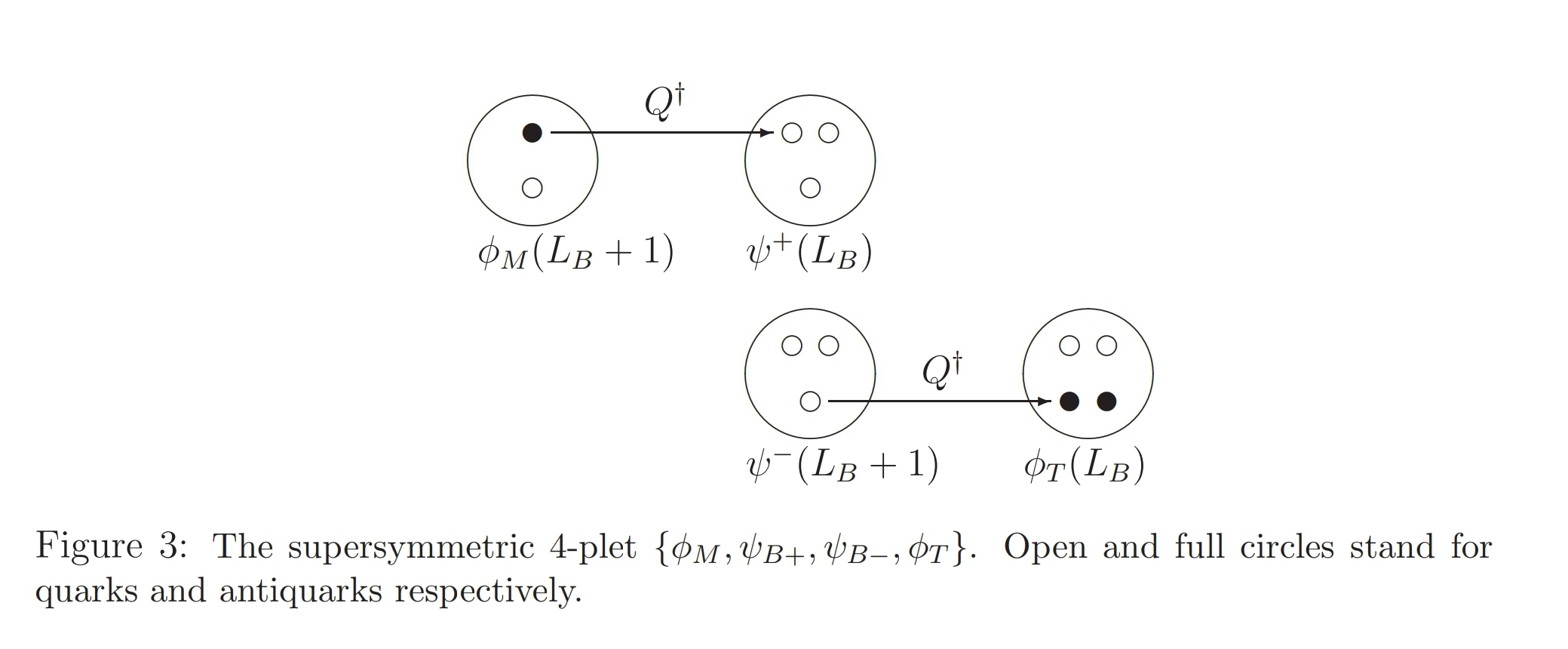
In the formulation of confined QCD as holographic light front QCD, this hadron supersymmetry is brought out explicitly by the fact that the light cone quantum mechanics of the system refines to supersymmetric quantum mechanics (dTDB 14, see e.g. Nielsen & Brodsky 2018).
This supersymmetry would be an exact symmetry of quantum hadrodynamics if antiquarks and diquarks had not only the same color charge but also the same mass (and other properties), for instance if the quarks involved all had vanishing mass, as assumed, to lowest order, in chiral perturbation theory. Any discrepancy causes breaking of the symmetry, hence here: supersymmetry breaking.
Phenomenology
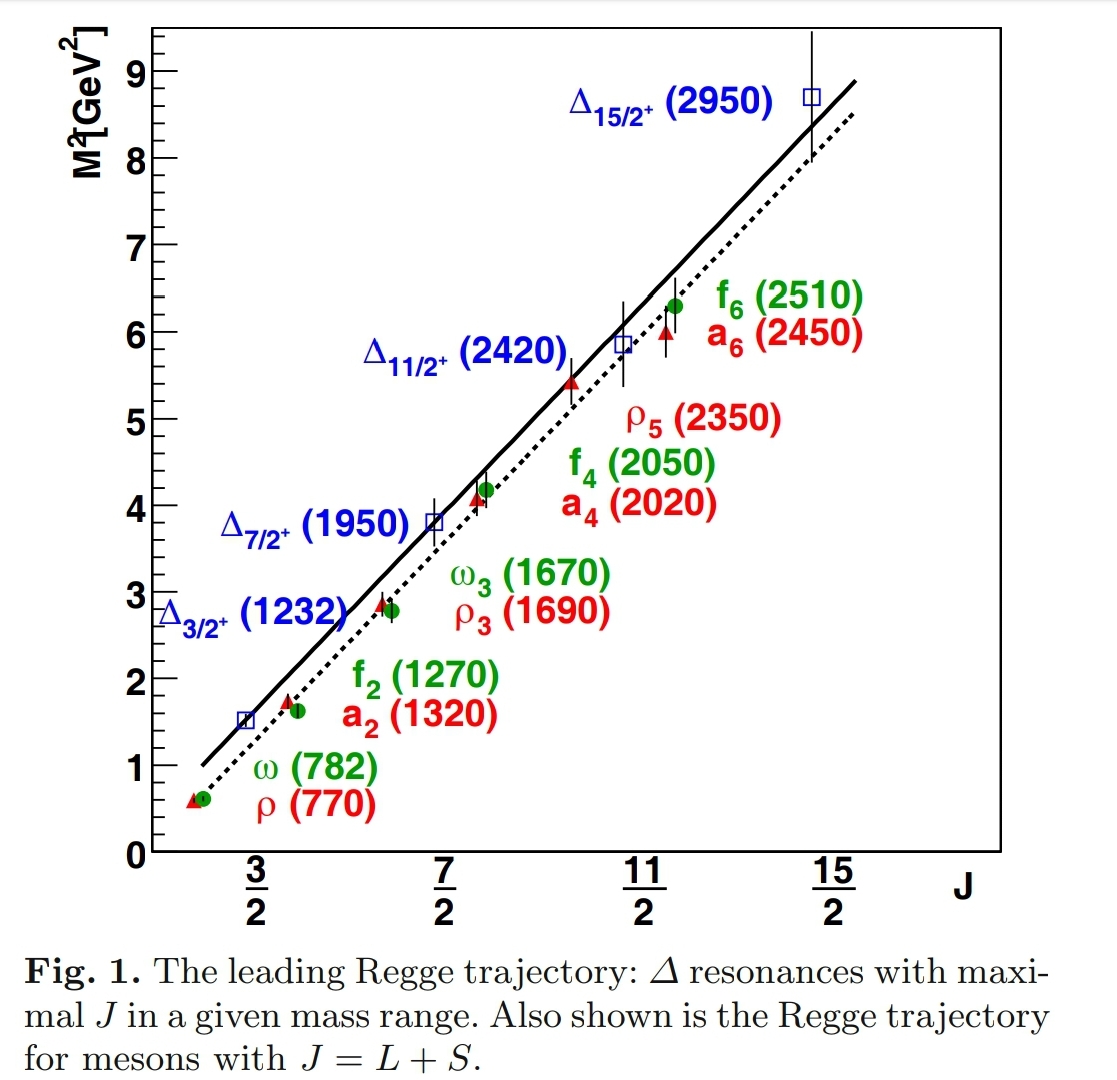
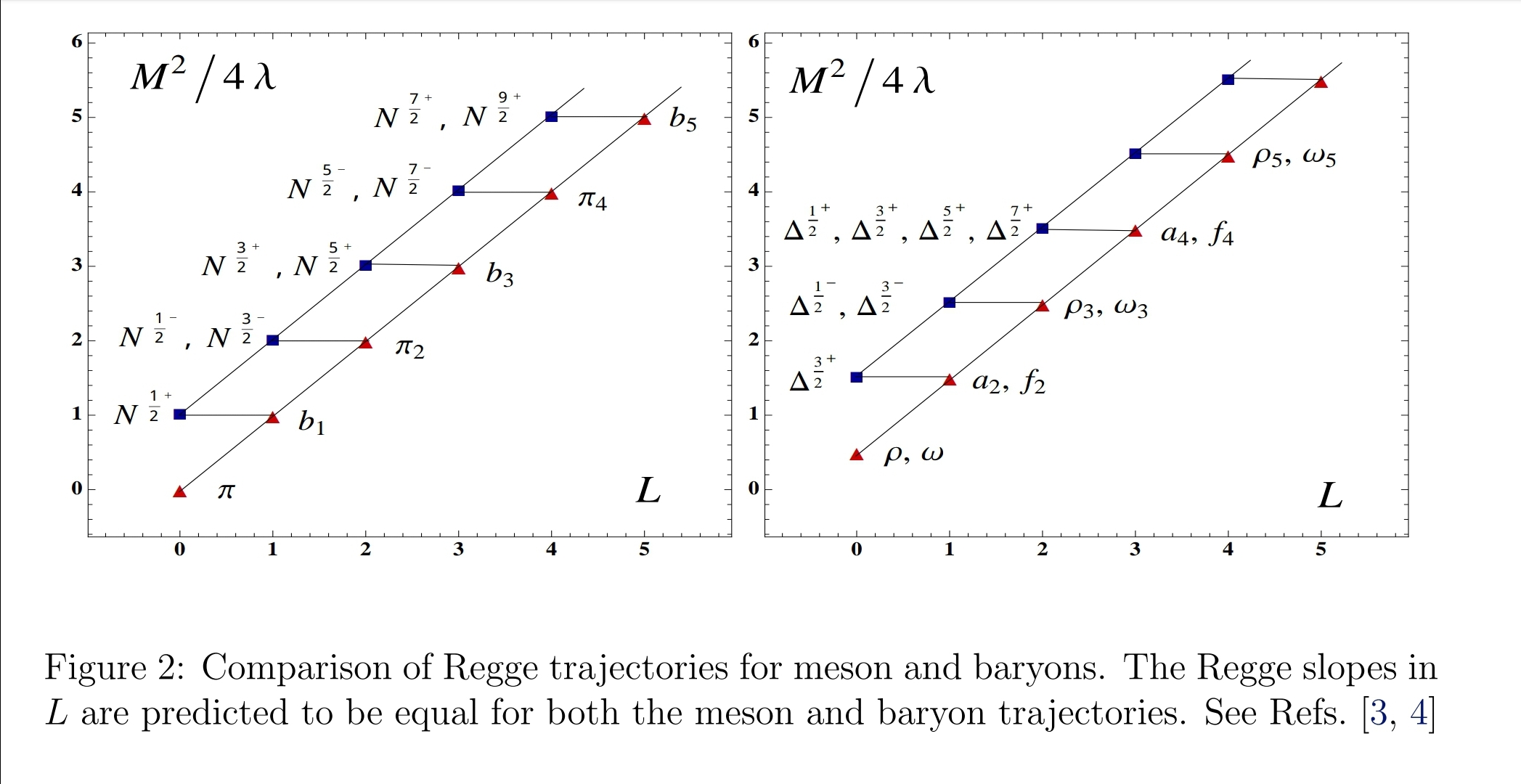
A direct consequence of hadron supersymmetry is the equality of slopes of the Regge trajectories of mesons and baryons. This is indeed observed in experiment, with high accuracy:
Related concepts
References
Original articles
The phenomenon of hadron supersymmetry was first noted and formalized (together with early classification of supersymmetry super Lie algebras) in:
-
Hironari Miyazawa, Baryon Number Changing Currents, Prog. Theor. Phys. 36 (1966) 6, 1266-1276 (spire:1235194, doi:10.1143/PTP.36.1266)
-
Hironari Miyazawa, Spinor Currents and Symmetries of Baryons and Mesons, Phys. Rev. 170, 1586 (1968) (doi:10.1103/PhysRev.170.1586)
In view of diquark models:
- Don B. Lichtenberg, Baryon Supermultiplets of in a Quark-Diquark Model, Phys. Rev. 178 (1969) 2197 (doi:10.1103/PhysRev.178.2197)
An argument that hadron supersymmetry is in fact implied by the constituent quark model in quantum chromodynamics:
-
Sultan Catto, Feza Gürsey, Algebraic treatment of effective supersymmetry, Nuov Cim A 86, 201–218 (1985) (doi:10.1007/BF02902548)
-
Sultan Catto, Feza Gürsey, New realizations of hadronic supersymmetry, Nuov Cim A 99, 685–699 (1988) (doi:10.1007/BF02730633)
-
Sultan Catto, Algebraic Realization of Quark-Diquark Supersymmetry (arXiv:hep-th/9811069, spire:479005)
-
Sultan Catto, Yasemin Gürcan, A. Khalfan, L. Kurt, B. Nicolescu, E. Yu, Hadronic Supersymmetry from QCD, Ukrainian Journal of Physics, Vol. 64 No. 8 (2019) (doi:10.15407/ujpe64.8.672)
-
Sultan Catto, Yasemin Gürcan, B. Nicolescu, E. Yu, Effective Hadronic Supersymmetry from Quantum Chromodynamics, Ukrainian Journal of Physics, Vol 64 No 12 (2019) (doi:10.15407/ujpe64.12.1096)
Formulation via octonions:
- Sultan Catto, Yasemin Gürcan, Amish Khalfan and Levent Kurt, Algebraic formulation of hadronic supersymmetry based on octonions: new mass formulas and further applications, Journal of Physics: Conference Series, Volume 563, XXII International Conference on Integrable Systems and Quantum Symmetries (ISQS-22) 23–29 June 2014, Prague, Czech Republic (doi:10.1088/1742-6596/563/1/012006/meta)
See also:
- Čestmír Burdík, Sultan Catto, Yasemin Giircan, Amish Khalfan, V. Kato La, Enxi Yu: Generalized Four-Dimensional Effective Hadronic Supersymmetry based on QCD: New Results, Journal of Physics: Conference Series 1416 (2019) [doi:10.1088/1742-6596/1416/1/012008]
Review
Review of the original work Miyazawa 66, Miyazawa 68, Catto-Gürsey 85, Catto-Gürsey 88:
-
Mauro Anselmino, Enrico Predazzi, Svante Ekelin, Sverker Fredriksson, Don B. Lichtenberg, Chapter IX of: Diquarks, Rev. Mod. Phys. 65 (1993) 1199 (doi:10.1103/RevModPhys.65.1199)
-
Don Lichtenberg, Hadron Supersymmetry and Relations between Meson and Baryon Masses, In: Kursunoglu B.N., Mintz S.L., Perlmutter A. (eds.) Neutrino Mass, Dark Matter, Gravitational Waves, Monopole Condensation, and Light Cone Quantization, Springer 1996 (doi:10.1007/978-1-4899-1564-1_29)
-
Don Lichtenberg, Whither Hadron Supersymmetry?, Contribution to: International Conference on Orbis Scientiae 1999: Quantum Gravity, Generalized Theory of Gravitation and Superstring Theory Based Unification_ (28th Conference on High-Energy Physics and Cosmology Since 1964) (1999) 203-208
Review with emphasis on the formulation via holographic light front QCD:
-
Guy de Téramond, Superconformal and Supersymmetric Constraints to Hadron Masses in Light-Front Holographic QCD, talk at The Proton Mass: At the Heart of Most Visible Matter, Trento 2017 (pdf, pdf)
-
Stanley Brodsky, Hadron Spectroscopy and Dynamics from Light-Front Holography and Superconformal Algebra, Few-Body Syst 59, 83 (2018) (arXiv:1802.08552)
-
Stanley Brodsky, Color Confinement and Supersymmetric Properties of Hadron Physics from Light-Front Holography, International Conference on Beauty, Charm and Hyperon Hadrons (BEACH 2018) 17–23 June 2018, Peniche, Portugal (arXiv:1912.12578)
-
Guy de Téramond, Emergent phenomena in QCD: The holographic perspective [arXiv:2212.14028]
Exotic hadron phenomenology
Discussion of exotic hadron-phenomenology using broken hadron supersymmetry:
-
Don Lichtenberg, Renato Roncaglia, Enrico Predazzi, Predicting exotic hadron masses from supersymmetry and a quark – diquark model, J. Phys. G: Nucl. Part. Phys. 23 (1997) 865 (doi:10.1088/0954-3899/23/8/001)
-
Harry J. Lipkin, Exotic Hadrons in the Constituent Quark Model, Prog. Theor. Phys. Suppl. 168 (2007) 15-22 (arXiv:hep-ph/0703190, doi:10.1143/PTPS.168.15)
Specifically regarding tetraquarks:
-
Hans Günter Dosch, Stanley Brodsky, Guy de Teramond, Marina Nielsen, Liping Zou, Exotic States in a Holographic Theory (arXiv:2012.02496)
-
M. A. Bedolla, J. Ferretti, C. D. Roberts, E. Santopinto, Spectrum of fully-heavy tetraquarks from a diquark+antidiquark perspective (arXiv:1911.00960, doi:10.1140/epjc/s10052-020-08579-3)
(in view of experimental results in 2021)
Via holographic light front QCD
Discussion of hadron supersymmetry via light cone supersymmetric quantum mechanics in holographic light front QCD:
-
Guy de Teramond, Hans Günter Dosch, Stanley Brodsky, Baryon Spectrum from Superconformal Quantum Mechanics and its Light-Front Holographic Embedding, Phys. Rev. D 91, 045040 (2015) (arXiv:1411.5243)
-
Hans Günter Dosch, Guy de Teramond, Stanley Brodsky, Superconformal Baryon-Meson Symmetry and Light-Front Holographic QCD, Phys. Rev. D 91, 085016 (2015) (arXiv:1501.00959)
-
Hans Günter Dosch, Guy de Teramond, Stanley Brodsky, Supersymmetry Across the Light and Heavy-Light Hadronic Spectrum, Phys. Rev. D 92, 074010 (2015) (arXiv:1504.05112)
-
Alexandre Deur, Stanley Brodsky, Guy de Teramond, Section 4.2 of: The QCD Running Coupling, Prog. Part. Nuc. Phys. 90 1 (2016) (arXiv:1604.08082, doi:10.1016/j.ppnp.2016.04.003)
-
Stanley Brodsky, Guy de Téramond, Hans Günter Dosch, Cédric Lorcé, Meson/Baryon/Tetraquark Supersymmetry from Superconformal Algebra and Light-Front Holography, International Journal of Modern Physics AVol. 31, No. 19, 1630029 (2016) (arXiv:1606.04638)
-
Hans Günter Dosch, Guy de Teramond, Stanley Brodsky, Supersymmetry Across the Light and Heavy-Light Hadronic Spectrum II, Phys. Rev. D 95, 034016 (2017) (arXiv:1612.02370)
-
Marina Nielsen, Stanley Brodsky, Hadronic Superpartners from Superconformal and Supersymmetric Algebra, Phys. Rev. D 97, 114001 (2018) (arXiv:1802.09652, doi:10.1103/PhysRevD.97.114001)
-
Marina Nielsen, Stanley Brodsky, Guy de Téramond, Hans Günter Dosch, Fernando S. Navarra, Liping Zou, Supersymmetry in the Double-Heavy Hadronic Spectrum, Phys. Rev. D 98, 034002 (2018) (arXiv:1805.11567)
-
Stanley Brodsky, Supersymmetric and Other Novel Features of Hadron Physics from Light-Front Holography, Proceedings of the 24th Workshop, “What Comes Beyond the Standard Models” (arXiv:2112.02453)
Last revised on July 9, 2025 at 16:26:54. See the history of this page for a list of all contributions to it.