nLab monopole

Contents

Context

Physics

Cosmic monopoles
Examples

Magnetic monopoles

Dirac monopole
Kaluza-Klein monopole
Yang monopole and ‘t Hooft monopole

Electroweak monopoles

Related concepts
References

Cosmic monopoles

In a gauge theory with a degenerate vacuum (such as when a Higgs mechanism applies), the moduli space of vacua is the quotient $G/H$ (the coset) of the gauge group $G$ by the stabilizer subgroup $H \hookrightarrow G$ of any of these vacua (spontaneous symmetry breaking).

This means that gauge equivalence classes of vaccum configurations on a spacetime $X$ are given by homotopy classes of maps $X \to \Pi(G/H)$ (where the notation on the right denotes the underlying homotopy type of the coset space, $\Pi$ is the shape modality).

If spacetime is locally to be taken of the form $\mathbb{R} \times (\mathbb{R}^3 - D^3 \times \mathbb{R}^0)$ , hence with a 3-dimensional ball-like piece taken out, them homotopy classes of maps $X \to \Pi(G/H)$ are classified by the second homotopy group $\pi_2(G/H)$ . For a given nontrivial element here the correponding vacuum is said to contain a cosmic monopole defect. (“Cosmic” just because this effect is thought to be most relevant on scales of cosmology.)

In other words this means that the vacuum strcture changes continuously as one moves around the string, but has a singularity on the locus of the string itself.

For more see at QFT with defects the section Topological defects from spontaneously broken symmetry.

Examples

Magnetic monopoles

Dirac monopole

In the original Dirac charge quantization argument an electromagnetic field is considerd outside a given point in space (line in spacetime). Mathematically this just corresponds to considering electromagfnetism on the maifold $(\mathbb{R}^3-D^0) \times \mathbb{R}$ , but physically this may be taken to model a situation where there is a magnetic monopole defect in the vavuum structure. The Dirac monopole.

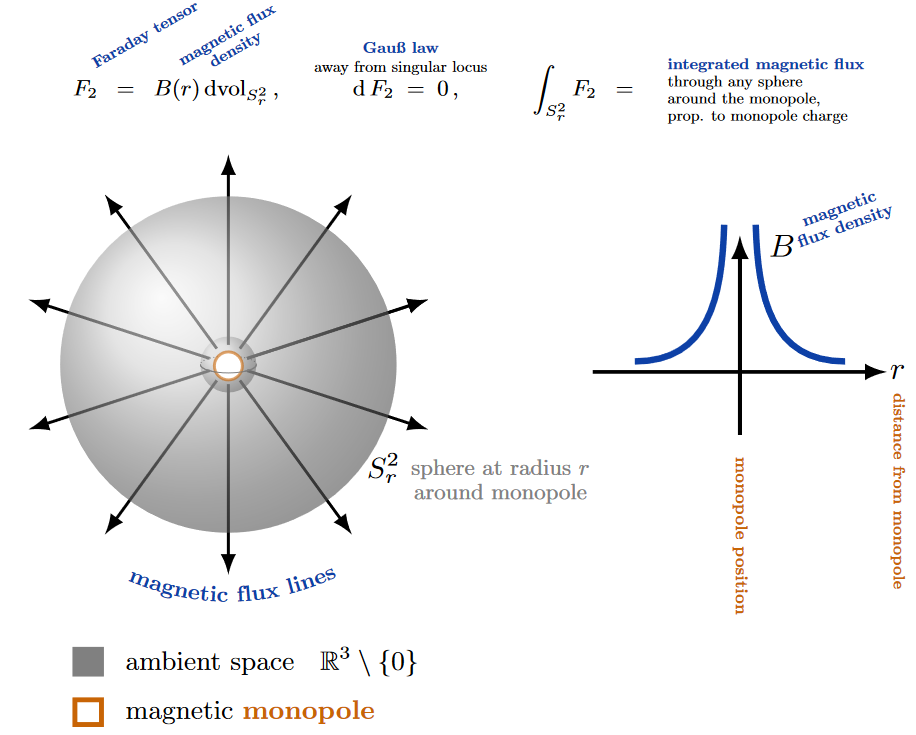
This is the classical example of monopoles and often taken to be the default meaning. (In the context of the standard model of particle physics, however, the default meaning is that of electroweak vacuum defect monopoles, discussed below.)

Technically, in the sense of the discussion at QFT with defects in the section Topological defects from spontaneous symmetry breaking what happens here is that the moduli space of the instanton sector of electromagnetism (= the classifying space of circle group-principal bundles) $B U(1)$ has the homotopy type of an Eilenberg-MacLane space $B U(1) \simeq K(\mathbb{Z},2)$ . This is by definition a space such that homotopy classes of continuous functions from a sphere into it are classified by the integers: $\pi_2(B U(1)) \simeq \mathbb{Z}$ .

But since there is a homotopy equivalence

(\mathbb{R}^3 - D^0)\times \mathbb{R} \simeq S^2

of Minkowski spacetime with the worldline of a point removes, this means precisely that the possible instanton field configurations of the electromagnetic field on such a spacetime is given by an integer. This integer is called the magnetic charge of the monopole defect. (Mathematically it is the first Chern class of the $U(1)$ -principal bundle which underlies the electromagnetic field).

Kaluza-Klein monopole

The gravitational incarnation of the Dirac monopole under Kaluza-Klein compactification is the Kaluza-Klein monopole. See there for more.

Yang monopole and ‘t Hooft monopole

The generalization of the Dirac monopole from $U(1)$ -Yang-Mills theory in 3+1 dimensional spacetime to $SU(2)$ -Yang-Mills theory in 5+1 dimensional spacetime is the Yang monopole.

With the Higgs field included, there is the 't Hooft-Polyakov monopole.

Electroweak monopoles

For a $G$ -gauge theory with spontaneous symmetry breaking of the vacuum from gauge group $G$ down to some subgroup $H \hookrightarrow G$ , monopole topological defects in the vacuum structure are classified by the second homotopy group $\pi_2(G/H)$ of the coset space (as explained at QFT with defects).

For the gauge theory of the electroweak force with its Higgs mechanism that is of relevance in the standard model of particle physics. This would mean that monopoles are classified by

\pi_2( (SU(2) \times U(1))_{ew} / U(1)_{em} ) \,.

However, in (Cho-Maison) it is claimed that the true topology of the moduli space of vacua in electroweak symmetry breaking is topologically more interesting. The corresponding phenomenology of vacuum defect monopoles of this kind is discussed in (Cho-Kim-Yoon13).

Related concepts

fields and particles in particle physics

and in the standard model of particle physics:

force field gauge bosons

photon - electromagnetic field (abelian Yang-Mills field)
W, Z, B-boson - electroweak field (Yang-Mills field)
gluon - strong nuclear force (Yang-Mills field)
graviton - field of gravity
infraparticle

scalar bosons

Higgs boson, inflaton (scalar field)

matter field fermions (spinors, Dirac fields)

flavors of fundamental fermions in the standard model of particle physics:
generation of fermions	1st generation	2nd generation	3d generation
quarks ( $q$ )
up-type	up quark ( $u$ )	charm quark ( $c$ )	top quark ( $t$ )
down-type	down quark ( $d$ )	strange quark ( $s$ )	bottom quark ( $b$ )
leptons
charged	electron	muon	tauon
neutral	electron neutrino	muon neutrino	tau neutrino

bound states:
mesons	light mesons: pion ( $u d$ ) ρ-meson ( $u d$ ) ω-meson ( $u d$ ) f1-meson a1-meson	strange-mesons: ϕ-meson ( $s \bar s$ ), kaon, K-meson ( $u s$ , $d s$ ) eta-meson ( $u u + d d + s s$ ) charmed heavy mesons*: D-meson ( $u c$ , $d c$ , $s c$ ) J/ψ-meson ( $c \bar c$ )	bottom heavy mesons: B-meson ( $q b$ ) ϒ-meson ( $b \bar b$ )
baryons	nucleons: proton $(u u d)$ neutron $(u d d)$