nLab shifted C-field flux quantization
Context
String theory
Ingredients
Critical string models
Extended objects
Topological strings
Backgrounds
Phenomenology
Cohomology
Special and general types
-
group cohomology, nonabelian group cohomology, Lie group cohomology
-
-
cohomology with constant coefficients / with a local system of coefficients
Special notions
Variants
-
differential cohomology
Extra structure
Operations
Theorems
Contents
Idea
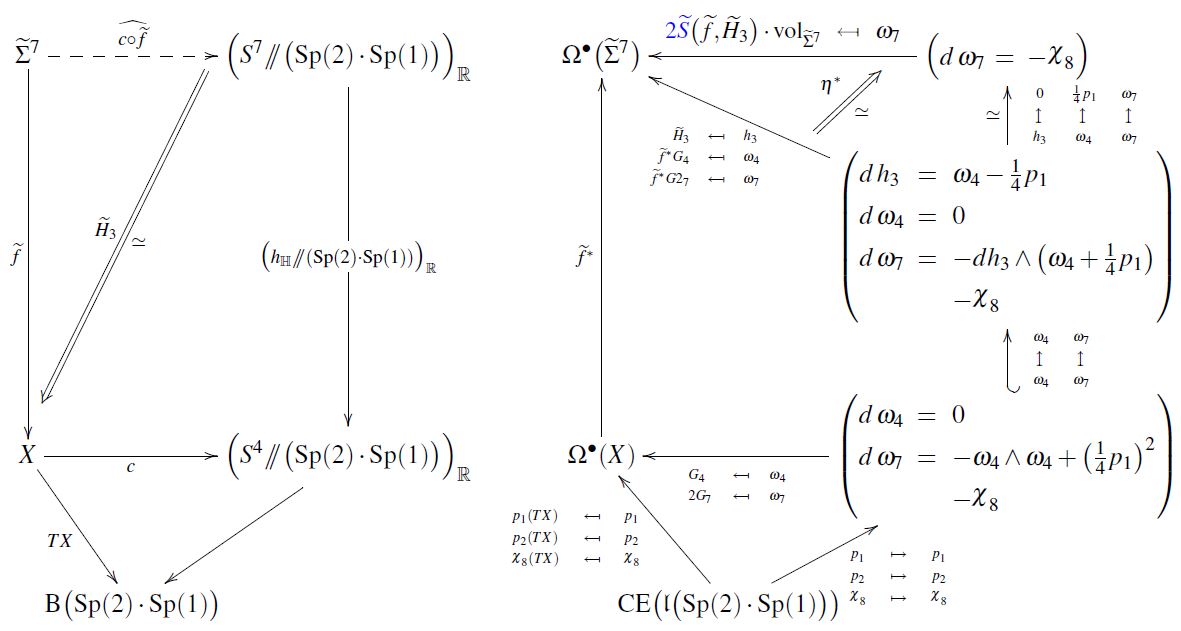
In string theory/M-theory, the shifted C-field flux quantization condition is a charge quantization-condition on the supergravity C-field expected in M-theory.
For the magnetic -flux
For the magnetic -flux, the shifted flux quantization says that the real cohomology class of the flux density (field strength) differential 4-form on spacetime becomes integral after shifted by one quarter of the first Pontryagin class, hence the condition that with the shifted 4-flux density defined as
(for any affine connection on spacetime, in particular the Levi-Civita connection) we have (using the de Rham theorem to translate from de Rham cohomology to real cohomology) that represents an integral cohomology-class:
This condition was originally argued for in (Witten 96a, Witten 96b) as a sufficient condition for ensuring that the prequantum line bundle for the 7d Chern-Simons theory on an M5-brane worldvolume is divisible by 2.
Proposals for encoding this condition by a Wu class-shifted variant of stable ordinary differential cohomology were considered in Hopkins-Singer 02, Diaconescu-Freed-Moore 03, FSS 12.
It turns out that the shifted flux quantization condition on the C-field is naturally implied (FSS1 19b, Prop. 4.12) by the requirement that is the differential form datum underlying, via Sullivan's theorem, a cocycle in unstable J- twisted Cohomotopy in degree 4 (Hypothesis H).
For the electric -flux
In the presence of non-vanishing C-field flux , the electric flux density of M2-branes is not alone, but receives corrections, first due to the quadratic C-field self-interaction in D=11 supergravity, but then also due to the shifted C-field flux quantization expected in M-theory:
The 11d supergravity literature states the corrected 7-flux to be the following combination, also known as the Page charge (due to Page 1983 (8), Duff & Stelle 1991, (43), reviewed e.g. in BLMP 13, p. 21):
where the second term subtracts the electric flux induced by the self-intersection of the field, and also ensures that the full expression is a closed differential form if the naive 11d supergravity equations of motion hold:
But in fact (2) does not quite make general sense, for two reasons:
-
In general is not an admissible condition and is not the actual vanshing of the C-field, due to the shifted C-field flux quantization.
-
Even if happens to be intregrally quantizaed (if is integral) the appearance of a globally defined C-field potential in (2),means that the total flux actually does vanish after all.
Charge-quantized -flux with shifted C-field flux quantization (FSS 19b, Prop. 4.3, FSS 19c, Section 4)
Both of these issues are solved if the C-field is taken to be charge quantized in J-twisted Cohomotopy (Hypothesis H). This gives the corrected formula
where
-
the expression lives on the homotopy pullback of the Sp(2)-parametrized quaternionic Hopf fibration
to spacetime, along the twisted Cohomotopy-cocycle that represents the C-field under Hypothesis H;
-
is the integral shifted C-field pulled back to that 3-spherical fibration over spacetime;
-
trivializes not the C-field itself, but its pullback, and not absolutely but relative to the background charge implied by shifted C-field flux quantization.
With the corrected 7-flux in twisted Cohomotopy it becomes true that
-
the integral of around the 7-sphere linking a black M2-brane is always integer (FSS 19c, Theorem 4.6);
-
this integer satisfies the C-field tadpole cancellation condition (FSS 19b, Section 4.6).
Related concepts
References
General
The suggestion originates in
-
Edward Witten, On Flux Quantization In M-Theory And The Effective Action, J. Geom. Phys. 22 1 (1997) 1-13 [arXiv:hep-th/9609122, doi:10.1016/S0393-0440(96)00042-3]
-
Edward Witten, Five-Brane Effective Action In M-Theory, J. Geom. Phys. 22 2 (1997) 103-133 [arXiv:hep-th/9610234, doi:10.1016/S0393-0440(97)80160-X]
Proposals to model the condition by a Wu class-shifted variant of ordinary differential cohomology include
-
Michael Hopkins, Isadore Singer, Quadratic Functions in Geometry, Topology, and M-Theory J. Differential Geom. Volume 70, Number 3 (2005), 329-452. (arXiv:math.AT/0211216, euclid:1143642908)
-
Duiliu-Emanuel Diaconescu, Dan Freed, Greg Moore, The -theory 3-form and -gauge theory, chapter in Haynes Miller, Douglas Ravenel (eds.) Elliptic Cohomology Geometry, Applications, and Higher Chromatic Analogues, Cambridge University Press (2007) [arXiv:hep-th/0312069, doi:10.1017/CBO9780511721489]
-
Dan Freed, Greg Moore, Setting the quantum integrand of M-theory, Communications in Mathematical Physics 263 1 (2006) 89-132 [arXiv:hep-th/0409135, doi:10.1007/s00220-005-1482-7]
-
Greg Moore, Anomalies, Gauss laws, and Page charges in M-theory, Comptes Rendus Physique 6 (2005) 251-259 [arXiv:hep-th/0409158, doi:10.1016/j.crhy.2004.12.005]
-
Domenico Fiorenza, Hisham Sati, Urs Schreiber, The moduli 3-stack of the C-field, Communications in Mathematical Physics, Volume 333, Issue 1 (2015), Page 117-151 (arXiv:1202.2455, doi:10.1007/s00220-014-2228-1)
Suggestion that an actual E8-principal bundle on 11d spacetime plays a role here:
-
D. Diaconescu, Gregory Moore, Edward Witten, Gauge Theory, and a Derivation of K-Theory from M-Theory, Adv. Theor. Math. Phys. 6:1031-1134, 2003 (arXiv:hep-th/0005090)
-
Allan Adams, Jarah Evslin, The loop group of and K-theory from 11d, JHEP 02 (2003) (arXiv:hep-th/0203218)
-
Hisham Sati, Gauge Theory and Gerbes in String Theory, Adv. Theor. Math. Phys. 14:1-39, 2010 (arXiv:hep-th/0608190)
The observation that the condition is implied by C-field charge quantization in J-twisted Cohomotopy (Hypothesis H):
-
Domenico Fiorenza, Hisham Sati, Urs Schreiber, Twisted Cohomotopy implies M-theory anomaly cancellation,
Comm. Math. Phys. 377 (2020) 1961-2025 (doi:10.1007/s00220-020-03707-2, arXiv:1904.10207)
-
Domenico Fiorenza, Hisham Sati, Urs Schreiber, Twisted Cohomotopy implies M5 WZ term level quantization, Comm. Math. Phys. 384 403–432 (2021) (doi:10.1007/s00220-021-03951-0, arXiv:1906.07417)
surveyed in:
-
Domenico Fiorenza, Hisham Sati, Urs Schreiber, The Character Map in Nonabelian Cohomology — Twisted, Differential, Generalizaed, World Scientific (2023) [arXiv:2009.11909, doi:10.1142/13422]
-
Hisham Sati, Urs Schreiber, Introduction to Hypothesis H (here)
Discussion of the Page charge in relation to the Myers effect in M-theory for M2-branes polarizing into M5-branes of fuzzy 3-sphere-shape:
- Krzysztof Pilch, Alexander Tyukov, Nicholas Warner, Flowing to Higher Dimensions: A New Strongly-Coupled Phase on M2 Branes, JHEP11 (2015) 170 (arXiv:1506.01045)
Proof that C-field flux quantization in stable Cohomotopy implies the desired divisibility by 6 of the D=11 supergravity action functional:
- Daniel Grady: Cohomotopy and flux quantization in M-theory [arXiv:2505.24696]
Relation to Freed-Witten anomaly
On relating the Freed-Witten anomaly to the shifted C-field flux quantization:
On D4-branes:
- Edward Witten, Section 2 of: Duality Relations Among Topological Effects In String Theory, JHEP 0005:031, 2000 [arXiv:hep-th/9912086, doi:10.1088/1126-6708/2000/05/031]
On D6-branes:
-
Sergei Gukov, James Sparks, p. 21 of: M-Theory on Manifolds, Nucl. Phys. B 625 (2002) 3-69 [arXiv:hep-th/0109025, doi:10.1016/S0550-3213(02)00018-4]
-
James Sparks, Global Worldsheet Anomalies from M-Theory, JHEP 0408:037, 2004 (arXiv:hep-th/0310147)
In F-theory
Discussion in F-theory:
-
Andres Collinucci, Raffaele Savelli, On Flux Quantization in F-Theory, J. High Energ. Phys. 2012 15 (2012) [arXiv:1011.6388, doi:10.1007/JHEP02(2012)015]
-
Andres Collinucci, Raffaele Savelli, On Flux Quantization in F-Theory II: Unitary and Symplectic Gauge Groups, J. High Energ. Phys. 2012 94 (2012) [arXiv:1203.4542, doi:10.1007/JHEP08(2012)094]
-
Raffaele Savelli, Flux Quantization in F-theory and Freed-Witten anomaly, talk at StringMath (2012) [pdf, pdf]
Last revised on June 2, 2025 at 04:52:36. See the history of this page for a list of all contributions to it.