nLab 24 branes transverse to K3
Context
String theory
Ingredients
Critical string models
Extended objects
Topological strings
Backgrounds
Phenomenology
Contents
Idea
Several classes of string theory vacua require the presence of exactly 24 branes of codimension 4 transverse to a K3-surface-fiber; this happens notably:
-
in F-theory on an elliptically fibered K3-surface, which requires/implies the presence of 24 D7-branes (Sen 96, p. 5),
-
in HET-theory KK-compactified on a K3-surface with vanishing gauge field instanton number, which requires/implies the presence of 24 NS5-branes (Schwarz 96, p. 50).
In both cases the condition arises as a kind of tadpole cancellation-condition, where the charge of the 24 branes in the compact K3-fiber space, which naively would be 24 in natural units, cancels out to zero, due to some subtle effect.
Despite the superficial similarity, this subtle effect is, at the face of it, rather different in the two cases:
-
for F-theory it results from the Kodeira classification of elliptic fibrations, which implies that an elliptically fibered K3 has exactly 24 singular points, counted with multiplicity,
-
for HET-theory it results, via the Green-Schwarz mechanism, from the Euler characteristic of a K3-surface being 24, and hence vanishing, via the Poincare-Hopf theorem, after the locus of 24 NS5-brane loci are cut out.
An argument that these two different-looking mechanisms are in fact equivalent, under suitable duality in string theory, is given in Braun-Brodie-Lukas-Ruehle 18, Sec. III, following detailed analysis due to Aspinwall-Morrison 97.
In F-theory on K3
In passing from M-theory to type IIA string theory, the locus of any Kaluza-Klein monopole in 11d becomes the locus of D6-branes in 10d. The locus of the Kaluza-Klein monopole in turn (as discussed there) is the locus where the -circle fibration degenerates. Hence in F-theory this is the locus where the fiber of the -elliptic fibration degenerates to the nodal curve. Since the T-dual of D6-branes are D7-branes, it follows that D7-branes in F-theory “are” the singular locus of the elliptic fibration.
Now, considering F-theory on K3, an elliptically fibered complex K3-surface
may be parameterized via the Weierstrass elliptic function as the solution locus of the equation
for , with a polynomial of degree 8 and of degree twelve. The j-invariant of the complex elliptic curve which this parameterizes for given is
The poles of the j-invariant correspond to the nodal curve, and hence it is at these poles that the D7-branes are located.
Since the order of the poles is 24 (the polynomial degree of the discriminant , see at elliptically fibered K3-surface – singular points) there are necessarily 24 D7-branes (Sen 96, page 5, Lerche 99, p. 6 , see also Morrison 04, sections 8 and 17, Denef 08, around (3.41), Douglas-Park-Schnell 14).
Notice that the net charge of these 24 D7-branes is supposed to vanish, due to S-duality effects (e.g. Denef 08, below (3.41)).
In IIA-theory on K3
Under T-duality the above discussion in F-theory translates to 24 D6-branes in type IIA string theory on K3 (Vafa 96, Footnote 2 on p. 6).
In HET-theory on K3
In heterotic string theory KK-compactified on K3 with vanishing gauge fields-instanton number, the existence of exactly 24 NS5-branes is implied by the Green-Schwarz mechanism: This requires that the 3-flux density measuring the NS5-brane charge satisfies ; and using that on K3 we have this implies, with Stokes' theorem, that the -flux through the 3-spheres around transversal NS5-brane-punctures of the K3 equals 24 (e.g. Schwarz 96, around p. 50, Aspinwall-Morrison 97, Sec. 4-5, Johnson 98, p. 30, Braun-Brodie-Lukas-Ruehle 18, Section III.A, Choi-Kobayashi 19, Sec. 1.1).
The duality of this HET-phenomenon with that in F-theory above is discussed in Braun-Brodie-Lukas-Ruehle 18, Section III.
Under Hypothesis H
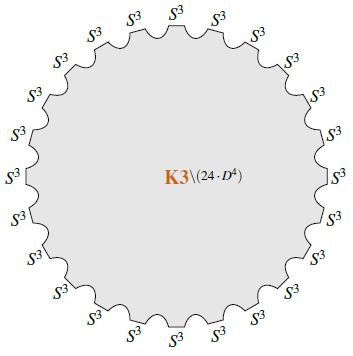
The vanishing of the Euler characteristic of K3 after cutting out the complement of 24 points is precisely the mechanism which witnesses the order 24 of the third stable homotopy group of spheres, seen under Pontryagin's theorem as the existence of a framed cobordism between 24 3-spheres:
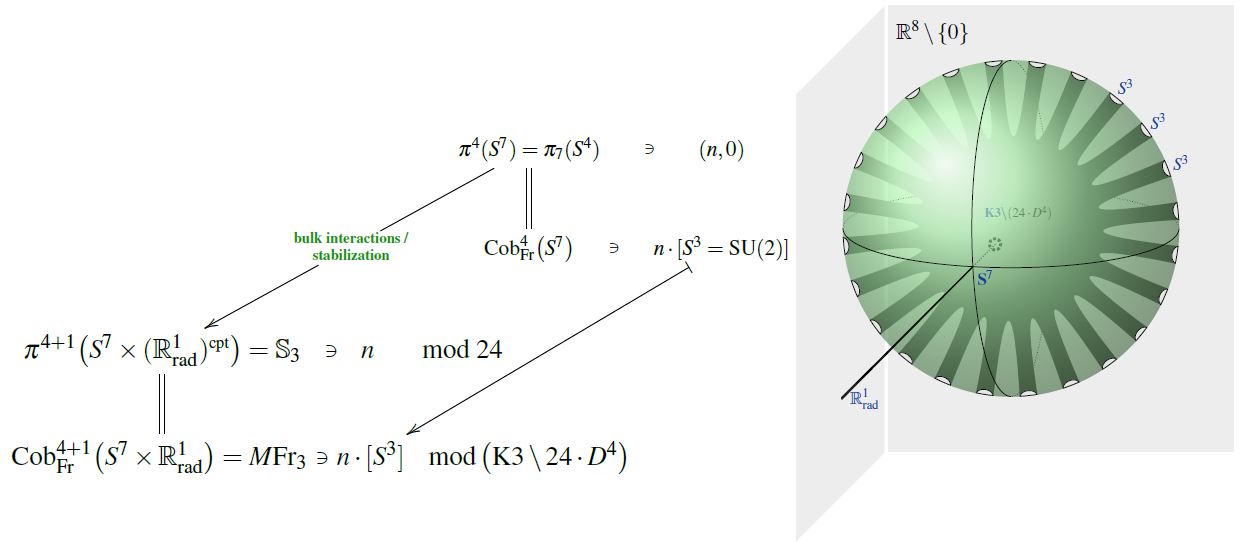
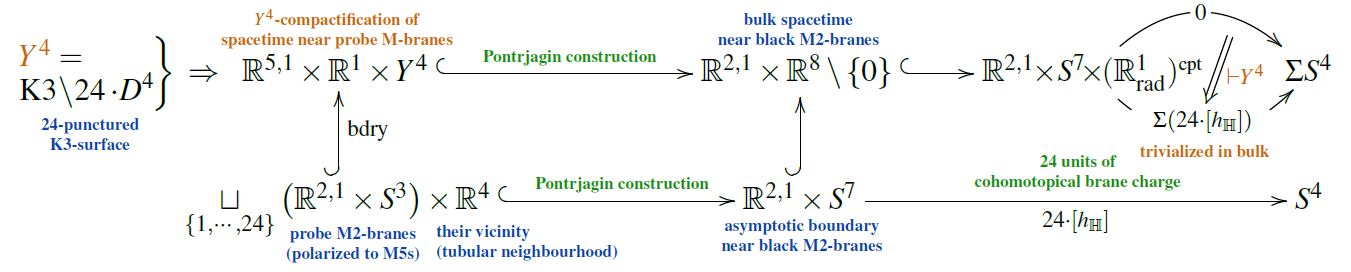
This relates the number of 24 branes transverse on K3 to Hypothesis H:
Related concepts
References
In F-theory
Discussion in F-theory via the Kodeira classification of elliptically fibered K3s:
-
Ashoke Sen, F-theory and Orientifolds, Nucl. Phys. B475:562-578, 1996 (arXiv:hep-th/9605150)
-
Wolfgang Lerche, p. 6 of: On the Heterotic/F-Theory Duality in Eight Dimensions, In: Baulieu L., Green M., Picco M., Windey P. (eds.) Progress in String Theory and M-Theory, NATO Science Series (Series C: Mathematical and Physical Sciences), vol 564. Springer 2001 (arXiv:hep-th/9910207, doi:10.1007/978-94-010-0852-5_2)
-
David Morrison, TASI Lectures on Compactification and Duality (arXiv:hep-th/0411120)
-
Frederik Denef, p. 34 of: Les Houches Lectures on Constructing String Vacua, in: String theory and the real world (arXiv:0803.1194, spire:780946)
-
Michael Douglas, Daniel S. Park, Christian Schnell, The Cremmer-Scherk Mechanism in F-theory Compactifications on K3 Manifolds, JHEP05 (2014) 135 (arXiv:1403.1595)
In HET-theory
Discussion in heterotic string theory via the Green-Schwarz mechanism on K3 (see also at small instantons):
-
John Schwarz, around p. 50 of: Lectures on Superstring and M Theory Dualities, Nucl. Phys. Proc. Suppl. 55B:1-32, 1997 (arXiv:hep-th/9607201)
-
Clifford Johnson, Études on D-Branes, in: Mike Duff et. al. (eds.) Nonperturbative aspects of strings, branes and supersymmetry, Proceedings, Trieste, Italy, March 23-April 3, 1998 (arXiv:hep-th/9812196, spire:481393)
-
Kang-Sin Choi, Tatsuo Kobayashi, Transitions of Orbifold Vacua, JHEP07 (2019) 111 (arXiv:1901.11194)
In F- and HET-theory
Joint discussion in F- and dual HET-theory:
-
Paul Aspinwall, David Morrison, Point-like Instantons on K3 Orbifolds, Nucl. Phys. B503 (1997) 533-564 (arXiv:hep-th/9705104, doi:10.1016/S0550-3213(97)00516-6)
-
Andreas Braun, Callum Brodie, Andre Lukas, Fabian Ruehle, NS5-Branes and Line Bundles in Heterotic/F-Theory Duality, Phys. Rev. D 98, 126004 (2018) (arXiv:1803.06190, doi:10.1103/PhysRevD.98.126004)
(in the context of heterotic line bundles)
Swampland cobordism conjecture
The swampland cobordism conjecture is the hypothesis that consistency of vacua in string theory/M-theory/F-theory (hence their being in the “landscape” instead of the “swampland”) requires (undefined) stringy/quantum gravity-analogs of cobordism groups to vanish:
-
Jacob McNamara, Cumrun Vafa, Cobordism Classes and the Swampland [arXiv:1909.10355, spire:1755441]
-
Miguel Montero, Cumrun Vafa, Cobordism Conjecture, Anomalies, and the String Lamppost Principle, J. High Energ. Phys. 2021, 63 (2021) [arXiv:2008.11729]
-
Markus Dierigl, Jonathan Heckman, On the Swampland Cobordism Conjecture and Non-Abelian Duality Groups, Physical Review D 2021 [arXiv:2012.00013]
-
Hirosi Ooguri, Tadashi Takayanagi, Cobordism Conjecture in AdS (arXiv:2006.13953)
-
David Andriot, Nils Carqueville, Niccolò Cribiori, Looking for structure in the cobordism conjecture, SciPost Phys. 13 (2022) 071 [arXiv:2204.00021, doi:10.21468/SciPostPhys.13.3.071]
-
Ralph Blumenhagen, Christian Kneissl, Chuying Wang, Dynamical Cobordism Conjecture: Solutions for End-of-the-World Branes, J. High Energ. Phys.2023 (2023) 123 [arXiv:2303.03423, doi:10.1007/JHEP05(2023)123]
-
Noah Braeger, Arun Debray, Markus Dierigl, Jonathan J. Heckman, Miguel Montero, Cobordism Utopia: U-Dualities, Bordisms, and the Swampland [arXiv:2505.15885]
Relation to topological K-theory and D-brane charge quantization in K-theory:
-
Ralph Blumenhagen, Niccolò Cribiori, Open-Closed Correspondence of K-theory and Cobordism, J. High Energ. Phys. 2022 37 (2022) [arXiv:2112.07678, doi:10.1007/JHEP08(2022)037]
-
Ralph Blumenhagen, Niccolò Cribiori, Christian Kneissl, Andriana Makridou, Dimensional Reduction of Cobordism and K-theory, Journal of High Energy Physics 2023, 181, [doi:10.1007/JHEP03(2023)181, arXiv:2208.01656]
Review:
- Ralph Blumenhagen, Nullifying Cobordism in Quantum Gravity, talk at QFT and Cobordism, CQTS (Mar 2023) web, slides: pdf, video: YT]
A more concrete consequence of this conjecture is claimed (McNamara & Vafa 2019, Sec. 5.2, 2nd paragr.) to be the statement that – paraphrasing/extrapolating somewhat (in line with Blumenhagen & Cribiori 2022; Blumenhagen et al. 2023; Blumenhagen 2023, p. 23): Certain topological brane charges are quantized in Cobordism cohomology; so that, in particular tadpole cancellation of brane charges is to happen in Cobordism cohomology. This kind of statement is also discussed, as a consequence of Hypothesis H, in (see p. 83):
- Hisham Sati, Urs Schreiber, M/F-Theory as Mf-Theory, Rev. Math. Phys. 35 10 (2023) [arXiv:2103.01877, doi:10.1142/S0129055X23500289]
Last revised on July 23, 2022 at 17:42:21. See the history of this page for a list of all contributions to it.