nLab Kaluza-Klein monopole
Context
Gravity
Formalism
Definition
Spacetime configurations
Properties
Spacetimes
| black hole spacetimes | vanishing angular momentum | positive angular momentum |
|---|---|---|
| vanishing charge | Schwarzschild spacetime | Kerr spacetime |
| positive charge | Reissner-Nordstrom spacetime | Kerr-Newman spacetime |
Quantum theory
Riemannian geometry
Contents
Idea
General
In the context of Kaluza-Klein theory where an electromagnetic field in Einstein-Maxwell theory in dimension is modeled by a configuration of pure Einstein gravity in dimension , a Kaluza-Klein monopole is a configuration of gravity in dimension which in dimension looks like a magnetic monopole (Sorkin 83, Gross-Perry 83).
In supergravity
This situation is of particular interest in the reduction of 11-dimensional supergravity (or M-theory, where one also speaks of the MK6-brane) where the Kaluza-Klein magnetic monopole charge is interpreted as D6-brane charge under duality between M-theory and type IIA string theory.
The Kaluza-Klein monopole (Han-Koh 85) is one type of solution of the equations of motion of 11-dimensional supergravity. It is given by the product of Euclidean Taub-NUT spacetime with Minkowski spacetime. Upon Kaluza-Klein compactification this looks like a monopole, whence the name. (For discussion as an ADE-singularity see IMSY 98, section 9, Asano 00, section 3.)
Upon KK-compactification on a 6-dimensional fiber, with the 11d KK-monopole / D6-brane completely wrapping the fiber, the KK-monopole in 11d supergravity becomes the KK-monopole in 5d supergravity. Further compactifying on a circle leads to a black hole in 4d, incarnated as a D0/D6 bound state (e.g. Nelson 93).
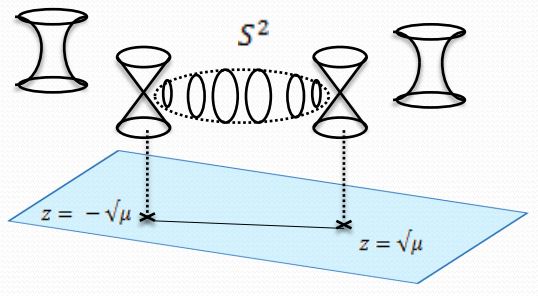
| geometry transverse to KK-monopoles | Riemannian metric | remarks |
|---|---|---|
| Taub-NUT space: geometry transverse to distinct KK-monopoles at | (e.g. Sen 97b, Sect. 2) | |
| ALE space Taub-NUT close to close-by KK-monopoles e.g. close to : | e.g. via Euler angles: (e.g. Asano 00, Sect. 2) | |
| -type ADE singularity: ALE space in the limit where all KK-monopoles coincide at | (e.g. Asano 00, Sect. 3) |
Properties
(For the moment the following is all about the KK-monopoles in 11d supergravity/M-theory.)
Far-horizon geometry
We discuss the far horizon geometry of coincident MK6-branes.
The metric tensor of coincident KK-monopoles in 11-dimensional supergravity in the limit that is
subject to the identification
This is equation (47) in IMSY 98, which applies subject to the condition
from a few lines above. Inserting this condition into the definition right above (47) shows that
hence that the distance from the locus of the MK6-brane is large in units of
The identification (2) means that this is the orbifold metric cone , hence an A-type ADE-singularity. To make this more explicit, introduce the complex coordinates
on , in terms of which (1) becomes
and which exhibit the identification (2) as indeed that of the A-type -action (Asano 00, around (18)).
Relation to the D6-brane in type IIA string theory
Under the relation between M-theory and type IIA superstring theory an ADE orbifold of the 11d KK-monopole corresponds to D6-branes combined with O6-planes (Townsend 95, p. 6, Atiyah-Witten 01, p. 17-18 see also e.g. Berglund-Brandhuber 02, around p. 15).
By (Townsend 95, (1), Sen 97c (1)-(4)) the 11d spacetime describing the KK-monopole lift of a plain single D6 brane is with metric tensor away from the origin of the -factor (which is the locus of the lifted D6/monopole) being
where
-
is any 3-form on satisfying ;
-
denotes the distance in from the origin.
-
is the charge of the monopole.
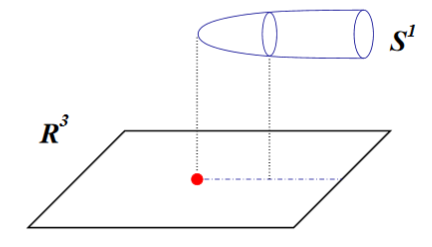
Away from this gives a circle bundle with first Chern class measured by the integral of (the RR-field of the D0-brane) over any sphere surrounding the singular locus in . By the electric-magnetic duality between D0-branes and D6-branes (due to the self-duality of the RR-field) this means, from the 10-dimensional perspective, that at a D6-brane is located.
graphics grabbed from Acharya-Gukov 04
Notice that the circle bundle away from its degeneration locus as a bundle over is necessarily of the form , a multiple of the complex Hopf fibration (see also Atiyah-Maldacena-Vafa 00, p. 10).
Discussion as an A-type ADE singularity is in (Sen 97c, section 2). Generalization to D-type singularities and hence D6-branes in orientifolds is in (Sen 97c ,section 3). Discussion as the fixed point of the circle group-action on the M-theory circle fibers is in (Townsend 95, p. 6, Atiyah-Witten 01, pages 17-18). Witten emphasizes that it is important that the location of the D6 is not just a cyclic group orbifold singularity but really a circle group-action fixed point conical singularity:
Chiral fermions arise when the locus of A−D−E singularities passes through isolated points at which X has an isolated conical singularity that is not just an orbifold singularity (Witten 01, p. 2).
Discussion dealing carefully with the perspective where the locus of the D6-brane is not remived: Gaillard & Schmude 09.
For more on this see at D6-brane – Relation to other branes and at M-theory lift of gauge enhancement on D6-branes.
Relation to the D7-brane in type IIB string theory/F-theory
Under further T-duality to type IIB superstring theory/F-theory these D6-branes become the D7-branes.
from M-branes to F-branes: superstrings, D-branes and NS5-branes
(e.g. Johnson 97, Blumenhagen 10)
Other Brane charges (?)
Hull 1997 argued (around equation 2.12) that the KK-monopole in 11-dimensional supergravity is the object which carries the 6-form charge Poincaré dual to the time-component of the 5-form charge of the M5-brane as appearing in the M-theory super Lie algebra, via
(An analogous relation identifies the time-component of the M2-brane charge with the charge of the M9-brane, see there.)
Related concepts
References
In 5d gravity
Original articles:
-
Rafael Sorkin, Kaluza-Klein monopole, Phys. Rev. Lett. 51 (1983) 87 (doi:10.1103/PhysRevLett.51.87)
-
David Gross, Malcolm Perry, Magnetic Monopoles in Kaluza-Klein Theories, Nucl. Phys. B226 (1983) 29 (doi:10.1016/0550-3213(83)90462-5)
-
P. J. Ruback, The motion of Kaluza-Klein monopoles, Comm. Math. Phys. Volume 107, Number 1 (1986), 93-102 (euclid:1104115933)
-
A. L. Cavalcanti de Oliveira, E. R. Bezerra de Mello, Kaluza-Klein Magnetic Monopole in Five-Dimensional Global Monopole Spacetime, Class. Quant. Grav. 21 (2004) 1685-1694 (arXiv:hep-th/0309189)
Review includes
- Emre Sakarya, Kaluza-Klein monopole, 2007 (pdf)
Discussion of topological T-duality for KK-monopoles is in
- Ashwin S. Pande, Topological T-duality and Kaluza-Klein Monopoles, Adv. Theor. Math. Phys., 12, (2007), pp 185-215 (arXiv:math-ph/0612034)
In 11d supergravity
Original articles
-
Seung Kee Han, I. G. Koh, Remaining Supersymmetry in Kaluza-Klein Monopole Background in D=11 Supergravity Theory, Phys.Rev. D31 (1985) 2503, in Michael Duff (ed.), The World in Eleven Dimensions 57-60 (doi:10.1103/PhysRevD.31.2503, spire:204521)
-
Paul Townsend, The eleven-dimensional supermembrane revisited, Phys. Lett. B 350 (1995) 184-187 [arXiv:hep-th/9501068]
-
Chris Hull: Gravitational Duality, Branes and Charges, Nucl. Phys. B 509 (1998) 216-251 [arXiv:hep-th/9705162, doi:10.1016/S0550-3213(97)00501-4]
-
Ashoke Sen, Kaluza-Klein Dyons in String Theory, Phys. Rev. Lett. 79:1619-1621, 1997 (arXiv:hep-th/9705212)
-
Ashoke Sen, Dynamics of Multiple Kaluza-Klein Monopoles in M- and String Theory, Adv. Theor. Math. Phys. 1:115-126, 1998 (arXiv:hep-th/9707042)
-
Ashoke Sen, A Note on Enhanced Gauge Symmetries in M- and String Theory, JHEP 9709:001,1997 (arXiv:hep-th/9707123)
-
Nissan Itzhaki, Juan Maldacena, Jacob Sonnenschein, Shimon Yankielowicz, Supergravity and The Large Limit of Theories With Sixteen Supercharges, Phys. Rev. D 58, 046004 1998 (arXiv:hep-th/9802042)
-
Masako Asano, Compactification and Identification of Branes in the Kaluza-Klein monopole backgrounds (arXiv:hep-th/0003241)
-
Michael Atiyah, Juan Maldacena, Cumrun Vafa, An M-theory Flop as a Large N Duality, J.Math.Phys.42:3209-3220,2001 (arXiv:hep-th/0011256)
-
Michael Atiyah, Edward Witten -Theory dynamics on a manifold of -holonomy, Adv. Theor. Math. Phys. 6 (2001) (arXiv:hep-th/0107177)
-
Edward Witten, Anomaly Cancellation On Manifolds Of Holonomy (arXiv:hep-th/0108165)
-
Per Berglund, Andreas Brandhuber, Matter From Manifolds, Nucl.Phys. B641 (2002) 351-375 (arXivLhep-th/0205184)
-
Jérôme Gaillard, Johannes Schmude, The lift of type IIA supergravity with D6 sources: M-theory with torsion, JHEP 1002:032,2010 (arXiv:0908.0305)
Discussion for the massive case, reducing to the D6-brane in massive type IIA string theory:
- Eric Bergshoeff, Eduardo Eyras, Yolanda Lozano, The massive Kaluza-Klein monopole, Physics Letters B
430 1–2 (1998) 77-86 [doi:10.1016/S0370-2693(98)00501-2, arXiv:hep-th/9802199]
Discussion in terms of G-structures:
- Ulf Danielsson, Giuseppe Dibitetto, Adolfo Guarino, KK-monopoles and -structures in M-theory/type IIA reductions, JHEP 1502 (2015) 096 (arXiv:1411.0575)
Discussion of a BFSS-like matrix model for MK6-branes:
- Amihay Hanany, Gilad Lifschytz, M(atrix) Theory on and a m(atrix) Theory Description of KK Monopoles, Nucl. Phys. B519:195-213, 1998 (arXiv:hep-th/9708037)
Relation to massive type IIA string theory:
- Eduardo Eyras, Yolanda Lozano, The Kaluza-Klein Monopole in a Massive IIA Background, Nucl. Phys. B546 (1999) 197-218 [arXiv:hep-th/9812188, doi:10.1016/S0550-3213(99)00098-X]
Review
-
Clifford Johnson, section 10.5 of D-brane primer (arXiv:hep-th/0007170)
-
Katrin Becker, Melanie Becker, John Schwarz, p. 333 of String Theory and M-Theory: A Modern Introduction, 2007
-
Luis Ibáñez, Angel Uranga, section 6.3.3 of String Theory and Particle Physics – An Introduction to String Phenomenology, Cambridge University Press 2012
-
Bobby Acharya, Sergei Gukov, p. 45 of: M theory and Singularities of Exceptional Holonomy Manifolds, Phys. Rept. 392 (2004) 121-189 [arXiv:hep-th/0409191]
Relation to black holes
Relation to black holes in string theory
- William Nelson, Kaluza-Klein Black Holes in String Theory, Phys. Rev. D49:5302-5306, 1994 (arXiv:hep-th/9312058)
Last revised on September 15, 2024 at 08:15:17. See the history of this page for a list of all contributions to it.
 (
(