nLab duality between M/F-theory and heterotic string theory

This entry is about M-theory/F-theory compactified on K3-surfaces. For M-theory on MO9-planes see instead at Hořava-Witten theory.

---

Idea

A duality in string theory. The non-perturbative enhancement of duality between heterotic and type II string theory:

F-theory$\,$ “KK-compactified” on an elliptically fibered K3 with a section is supposed to be equivalent to heterotic string theory KK-compactified on a 2-torus.

More generally, F-theory on a complex $n$-dimensional $X$ fibered $X\to B$ with elliptic K3-fibers is supposed to be equivalent to heterotic string theory on an elliptically fibered Calabi-Yau manifold $Z \to B$ of complex dimension $(n-1)$.

A detailed discussion of the equivalence of the respective moduli spaces is originally due to (Friedman-Morgan-Witten 97). A review of this is in (Donagi 98).

From the abstract of (Donagi 98).

The heterotic string compactified on an $(n-1)$-dimensional elliptically fibered Calabi-Yau $Z \to B$ is conjectured to be dual to F-theory compactified on an $n$-dimensional Calabi-Yau $X \to B$, fibered over the same base with elliptic K3 fibers. In particular, the moduli of the two theories should be isomorphic. The cases most relevant to the physics are $n=2$, $3$, $4$, i.e. the compactification is to dimensions $d=8$, $6$ or $4$ respectively. Mathematically, the richest picture seems to emerge for $n=3$, where the moduli space involves an analytically integrable system whose fibers admit rather different descriptions in the two theories.

Aspects

Singular locus of the elliptic fibration and 24 D7-branes

In passing from M-theory to type IIA string theory, the locus of any Kaluza-Klein monopole in 11d becomes the locus of D6-branes in 10d. The locus of the Kaluza-Klein monopole in turn (as discussed there) is the locus where the $S^1_A$-circle fibration degenerates. Hence in F-theory this is the locus where the fiber of the $S^1_A \times S^1_B$-elliptic fibration degenerates to the nodal curve. Since the T-dual of D6-branes are D7-branes, it follows that D7-branes in F-theory “are” the singular locus of the elliptic fibration.

Now an elliptically fibered complex K3-surface

$$\array{ T &\longrightarrow& K3 \\ && \downarrow \\ && \mathbb{C}\mathbb{P}^1 }$$

may be parameterized via the Weierstrass elliptic function as the solution locus of the equation

$$y^2 = x^3 + f(z) x + g(z)$$

for $x,y,z \in \mathbb{C}\mathbb{P}^1$, with $f$ a polynomial of degree 8 and $g$ of degree twelve. The j-invariant of the complex elliptic curve which this parameterizes for given $z$ is

$$j(\tau(z)) = \frac{4 (24 f)^3}{27 g^2 + 4 f^3} \,.$$

The poles $j\to \infty$ of the j-invariant correspond to the nodal curve, and hence it is at these poles that the D7-branes are located.

from SS21

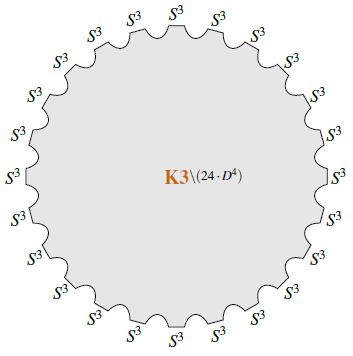
Since the order of the poles is 24 (the polynomial degree of the discriminant $\Delta = 27 g^2 + 4 f^3$, see at elliptically fibered K3-surface – singular points) there are necessarily 24 D7-branes (Sen 96, page 5, Sen 97b, see also Morrison 04, sections 8 and 17, Denef 08, around (3.41), Douglas-Park-Schnell 14).

Under T-duality this translates to 24 D6-branes in type IIA string theory on K3 (Vafa 96, Footnote 2 on p. 6).

Notice that the net charge of these 24 D7-branes is supposed to vanish, due to S-duality effects (e.g. Denef 08, below (3.41)).

(This reminds one of the situation for the third stable homotopy group of spheres…)

For analogous discussion of 24 NS5-branes in heterotic string theory on K3 see Schwarz 97, around p. 50.

For more see at 24 branes transverse to K3.

From M-branes to F-branes to heterotic strings and NS5-branes

from M-branes to F-branes: superstrings, D-branes and NS5-branes

M-theory on $S^1_A \times S^1_B$-elliptic fibration	KK-compactification on $S^1_A$	type IIA string theory	T-dual KK-compactification on $S^1_B$	type IIB string theory	geometrize the axio-dilaton	F-theory on elliptically fibered-K3 fibration	duality between F-theory and heterotic string theory	heterotic string theory on elliptic fibration
M2-brane wrapping $S_A^1$	double dimensional reduction $\mapsto$	type IIA superstring	$\mapsto$	type IIB superstring	$\mapsto$	“	$\mapsto$	heterotic superstring
M2-brane wrapping $S_B^1$	$\mapsto$	D2-brane	$\mapsto$	D1-brane	$\mapsto$	“
M2-brane wrapping $p$ times around $S_A^1$ and $q$ times around $S_B^1$	$\mapsto$	$p$ strings and $q$ D2-branes	$\mapsto$	(p,q)-string	$\mapsto$	“
M5-brane wrapping $S_A^1$	double dimensional reduction $\mapsto$	D4-brane	$\mapsto$	D5-brane	$\mapsto$	“
M5-brane wrapping $S_B^1$	$\mapsto$	NS5-brane	$\mapsto$	NS5-brane	$\mapsto$	“	$\mapsto$	NS5-brane
M5-brane wrapping $p$ times around $S_A^1$ and $q$ times around $S_B^1$	$\mapsto$	$p$ D4-brane and $q$ NS5-branes	$\mapsto$	(p,q)5-brane	$\mapsto$	“
M5-brane wrapping $S_A^1 \times S_B^1$	$\mapsto$		$\mapsto$	D3-brane	$\mapsto$	“
KK-monopole/A-type ADE singularity (degeneration locus of $S^1_A$-circle fibration, Sen limit of $S^1_A \times S^1_B$ elliptic fibration)	$\mapsto$	D6-brane	$\mapsto$	D7-branes	$\mapsto$	A-type nodal curve cycle degeneration locus of elliptic fibration (Sen 97, section 2)		SU-gauge enhancement
KK-monopole orientifold/D-type ADE singularity	$\mapsto$	D6-brane with O6-planes	$\mapsto$	D7-branes with O7-planes	$\mapsto$	D-type nodal curve cycle degeneration locus of elliptic fibration (Sen 97, section 3)		SO-gauge enhancement
exceptional ADE-singularity	$\mapsto$		$\mapsto$		$\mapsto$	exceptional ADE-singularity of elliptic fibration	$\mapsto$	E6-, E7-, E8-gauge enhancement

(e.g. Johnson 97, Blumenhagen 10)

Non-reducible heterotic $E_8$-gauge backgrounds

There are some F-theory backgrounds whose supposed dual in heterotic string theory involves an E8-principal connection which is not reducible to SemiSpin(16) (Distler-Sharpe 10, section 5), while in fact the traditional construction of the heterotic worldsheet theory only covers this case. In (Distler-Sharpe 10, section 7-8) it is argued that therefore a more general formulation of heterotic string theory needs to involve parameterized WZW models. See also at heterotic string – Properties – General gauge backgrounds and parameterized WZW models.

Related concepts

• 24 branes transverse to K3

F-theory KK-compactified on elliptically fibered complex analytic fiber $\Sigma$

$dim_{\mathbb{C}}(\Sigma)$	1	2	3	4	5
	F-theory	F-theory on CY2	F-theory on CY3	F-theory on CY4	F-theory on CY5

KK-compactification of M-theory

• M-theory on a circle

• M-theory on 8-manifolds/on Spin(7)-manifolds

• M-theory on G₂-manifolds

  • G₂-MSSM

• M-theory on Sp(1)-manifolds

• M-theory on hyperbolic manifolds

• heterotic M-theory on ADE-orbifolds

• M-theory on Calabi-Yau manifolds

  • on CY2-folds

  • on CY3-folds

  • on CY4-folds

  • on CY5-folds

References

For type IIA and M-theory

The conjectured duality between type IIA string theory KK-compactified on K3 times an n-torus and heterotic string theory on the $(n+2)$-torus is originally due to

• Chris Hull, Paul Townsend, section 6 of: Unity of Superstring Dualities, Nucl. Phys. B438:109-137, 1995 (arXiv:hep-th/9410167)

• Edward Witten, section 4 of: String Theory Dynamics In Various Dimensions, Nucl. Phys. B443:85-126, 1995 (arXiv:hep-th/9503124)

• Wolfgang Lerche, On the Heterotic/F-Theory Duality in Eight Dimensions, In: Baulieu L., Green M., Picco M., Windey P. (eds.) Progress in String Theory and M-Theory, NATO Science Series (Series C: Mathematical and Physical Sciences), vol 564. Springer 2001 (arXiv:hep-th/9910207, doi:10.1007/978-94-010-0852-5_2)

Review:

• Paul Aspinwall, David Morrison, String Theory on K3 Surfaces, in Brian Greene, Shing-Tung Yau (eds.), Mirror Symmetry II, International Press, Cambridge, 1997, pp. 703-716 (arXiv:hep-th/9404151)

• Paul Aspinwall, K3 Surfaces and String Duality, in Shing-Tung Yau (ed.): Differential geometry inspired by string theory 1-95 (arXiv:9611137 spire:426102)

Further discussion:

• Paul Aspinwall, Enhanced Gauge Symmetries and K3 Surfaces, Phys.Lett. B357 (1995) 329-334 (arXiv:hep-th/9507012)

• Eric Bergshoeff, C. Condeescu, G. Pradisi, F. Riccioni, Heterotic-Type II duality and wrapping rules, JHEP12(2013)057 (arXiv:1311.3578)

Specifically in relation to the putative K-theory-classification of D-brane charge:

• Inaki Garcia-Etxebarria, Angel Uranga, From F/M-theory to K-theory and back, JHEP 0602:008,2006 (arXiv:hep-th/0510073)

Specifically in M-theory on G₂-manifolds:

• Michael Atiyah, Edward Witten section 6.4 of $M$-Theory dynamics on a manifold of $G_2$-holonomy, Adv. Theor. Math. Phys. 6 (2001) (arXiv:hep-th/0107177)

• Bobby Acharya, Alex Kinsella, David Morrison, Non-Perturbative Heterotic Duals of M-Theory on $G_2$ Orbifolds (arXiv:2106.03886)

Specifically in relation to Moonshine:

• Miranda Cheng, Sarah M. Harrison, Roberto Volpato, Max Zimet, K3 String Theory, Lattices and Moonshine (arXiv:1612.04404)

For F-theory

Discussion for F-theory includes

• David Morrison, Cumrun Vafa, Compactifications of F-Theory on Calabi–Yau Threefolds – I, Nucl. Phys. B473 (1996) 74-92 (arXiv:hep-th/9602114)

• David Morrison, Cumrun Vafa, Compactifications of F-Theory on Calabi–Yau Threefolds – II, Nucl. Phys. B476:437-469, 1996 (arXiv:hep-th/9603161)

• Ashoke Sen, F-theory and Orientifolds (arXiv:hep-th/9605150)

• Robert Friedman, John Morgan, Edward Witten, Vector Bundles And F Theory, Commun.Math.Phys.187:679-743, 1997 (arXiv:hep-th/9701162)

• Paul Aspinwall, M-Theory Versus F-Theory Pictures of the Heterotic String, Adv.Theor.Math.Phys.1:127-147, 1998 (arXiv:hep-th/9707014)

Review of (Friedman-Morgan-Witten 97) is in

• Ron Donagi, ICMP lecture on heterotic/F-theory duality (arXiv:hep-th/9802093)

• Björn Andreas, $N=1$ Heterotic/F-theory duality, PhD thesis (pdf)

with more details in

• Ron Donagi, Eyal Markman, Spectral curves, algebraically completely integrable Hamiltonian systems, and moduli of bundles (arXiv:alg-geom/9507017)

The issue with non-reducible $E_8$-gauge connections is highligted in

• Jacques Distler, Eric Sharpe, section 5 of Heterotic compactifications with principal bundles for general groups and general levels, Adv. Theor. Math. Phys. 14:335-398, 2010 (arXiv:hep-th/0701244)

On a subtlety in the application of the Narasimhan-Seshadri theorem in the duality:

• Herbert Clemens, Stuart Raby, Heterotic/F-theory Duality and Narasimhan-Seshadri Equivalence (arxiv:1906.07238)

See also:

• Michael Douglas, Daniel S. Park, Christian Schnell, The Cremmer-Scherk Mechanism in F-theory Compactifications on K3 Manifolds, JHEP05 (2014) 135 (arXiv:1403.1595)

• Herbert Clemens, Stuart Raby, Heterotic/F-theory Duality and Narasimhan-Seshadri Equivalence [arXiv:1906.07238]

• Paul-Konstantin Oehlmann, Fabian Ruehle, Benjamin Sung, The Frozen Phase of Heterotic F-theory Duality [arXiv:2404.02191]

  (in relation to D=6 N=(1,0) SCFT)

For both

• Yusuke Kimura, New perspectives in the duality of M-theory, heterotic strings, and F-theory (arXiv:2103.03088)