nLab Euclidean G-space
Context
Topology
topology (point-set topology, point-free topology)
see also differential topology, algebraic topology, functional analysis and topological homotopy theory
Basic concepts
-
fiber space, space attachment
Extra stuff, structure, properties
-
Kolmogorov space, Hausdorff space, regular space, normal space
-
sequentially compact, countably compact, locally compact, sigma-compact, paracompact, countably paracompact, strongly compact
Examples
Basic statements
-
closed subspaces of compact Hausdorff spaces are equivalently compact subspaces
-
open subspaces of compact Hausdorff spaces are locally compact
-
compact spaces equivalently have converging subnet of every net
-
continuous metric space valued function on compact metric space is uniformly continuous
-
paracompact Hausdorff spaces equivalently admit subordinate partitions of unity
-
injective proper maps to locally compact spaces are equivalently the closed embeddings
-
locally compact and second-countable spaces are sigma-compact
Theorems
Analysis Theorems
Representation theory
geometric representation theory
Ingredients
Definitions
representation, 2-representation, ∞-representation
Geometric representation theory
-
Grothendieck group, lambda-ring, symmetric function, formal group
-
principal bundle, torsor, vector bundle, Atiyah Lie algebroid
-
Eilenberg-Moore category, algebra over an operad, actegory, crossed module
Theorems
Contents
Definition
Let be a compact Lie group and let be an orthogonal -linear representation on a real vector space . Then the underlying Euclidean space inherits the structure of a topological G-space
We may call this the Euclidean G-space associated with the linear representation .
Properties
Relation to representation spheres
The one-point compactification of a Euclidean -space is the corresponding representation sphere:
Relation to representation tori
Let be an orthogonal linear representation of a finite group on a real vector space .
If is the point group of a crystallographic group inside the Euclidean group
then the -action on the Euclidean -space descends to the quotient by the action of the translational normal subgroup lattice (this Prop.). The resulting -space is an n-torus with -action, which might be called the representation torus of
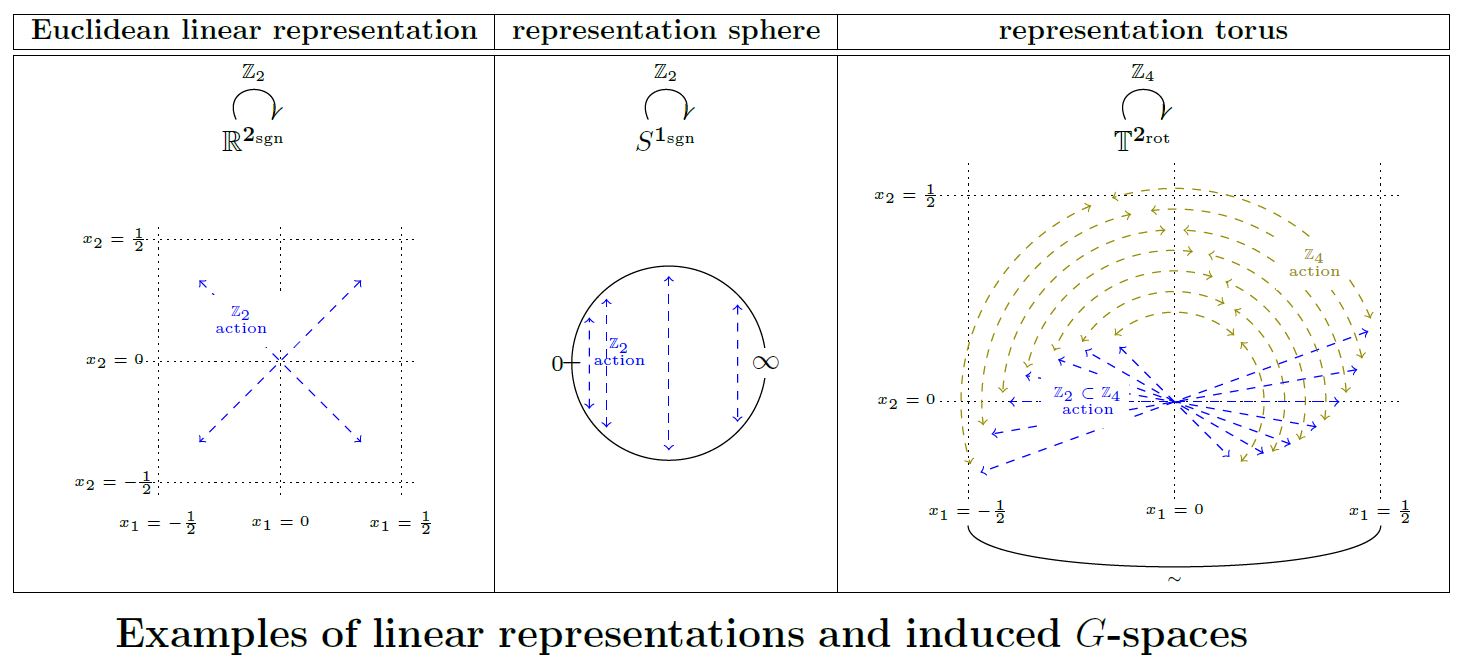
graphics grabbed from SS 19
Equivariant configurations in Euclidean -spaces
(…)
Related concepts
References
Discussion of equivariant configuration spaces of points in Euclidean -spaces:
- Colin Rourke, Brian Sanderson, Equivariant Configuration Spaces, J. London Math. Soc. 62 (2000) 544-552 (arXiv:math/9712216)
Created on October 29, 2019 at 09:40:01. See the history of this page for a list of all contributions to it.