nLab computation

Skip the Navigation Links | Home Page | All Pages | Latest Revisions | Discuss this page |
Redirected from "computers".
Contents

Context

Computability

constructive mathematics, realizability, computability

intuitionistic mathematics

propositions as types, proofs as programs, computational trinitarianism

Constructive mathematics

Realizability

Computability

Type theory

natural deduction metalanguage, practical foundations

  1. type formation rule
  2. term introduction rule
  3. term elimination rule
  4. computation rule

type theory (dependent, intensional, observational type theory, homotopy type theory)

syntax object language

computational trinitarianism =
propositions as types +programs as proofs +relation type theory/category theory

logicset theory (internal logic of)category theorytype theory
propositionsetobjecttype
predicatefamily of setsdisplay morphismdependent type
proofelementgeneralized elementterm/program
cut rulecomposition of classifying morphisms / pullback of display mapssubstitution
introduction rule for implicationcounit for hom-tensor adjunctionlambda
elimination rule for implicationunit for hom-tensor adjunctionapplication
cut elimination for implicationone of the zigzag identities for hom-tensor adjunctionbeta reduction
identity elimination for implicationthe other zigzag identity for hom-tensor adjunctioneta conversion
truesingletonterminal object/(-2)-truncated objecth-level 0-type/unit type
falseempty setinitial objectempty type
proposition, truth valuesubsingletonsubterminal object/(-1)-truncated objecth-proposition, mere proposition
logical conjunctioncartesian productproductproduct type
disjunctiondisjoint union (support of)coproduct ((-1)-truncation of)sum type (bracket type of)
implicationfunction set (into subsingleton)internal hom (into subterminal object)function type (into h-proposition)
negationfunction set into empty setinternal hom into initial objectfunction type into empty type
universal quantificationindexed cartesian product (of family of subsingletons)dependent product (of family of subterminal objects)dependent product type (of family of h-propositions)
existential quantificationindexed disjoint union (support of)dependent sum ((-1)-truncation of)dependent sum type (bracket type of)
logical equivalencebijection setobject of isomorphismsequivalence type
support setsupport object/(-1)-truncationpropositional truncation/bracket type
n-image of morphism into terminal object/n-truncationn-truncation modality
equalitydiagonal function/diagonal subset/diagonal relationpath space objectidentity type/path type
completely presented setsetdiscrete object/0-truncated objecth-level 2-type/set/h-set
setset with equivalence relationinternal 0-groupoidBishop set/setoid with its pseudo-equivalence relation an actual equivalence relation
equivalence class/quotient setquotientquotient type
inductioncolimitinductive type, W-type, M-type
higher inductionhigher colimithigher inductive type
-0-truncated higher colimitquotient inductive type
coinductionlimitcoinductive type
presettype without identity types
set of truth valuessubobject classifiertype of propositions
domain of discourseuniverseobject classifiertype universe
modalityclosure operator, (idempotent) monadmodal type theory, monad (in computer science)
linear logic(symmetric, closed) monoidal categorylinear type theory/quantum computation
proof netstring diagramquantum circuit
(absence of) contraction rule(absence of) diagonalno-cloning theorem
synthetic mathematicsdomain specific embedded programming language

homotopy levels

semantics

Deduction and Induction

Foundations

foundations

The basis of it all

 Set theory

set theory

Foundational axioms

foundational axioms

Removing axioms

Contents

Idea

A program. A construction of a term of some type. The topic of computability theory.

computability

type I computabilitytype II computability
typical domainnatural numbers ℕ\mathbb{N}Baire space of infinite sequences 𝔹=ℕ ℕ\mathbb{B} = \mathbb{N}^{\mathbb{N}}
computable functionspartial recursive functioncomputable function (analysis)
type of computable mathematicsrecursive mathematicscomputable analysis, Type Two Theory of Effectivity
type of realizabilitynumber realizabilityfunction realizability
partial combinatory algebraKleene's first partial combinatory algebraKleene's second partial combinatory algebra

References

General

On the theory of computation and introducing the notion of denotational semantics of programming languages:

  • Dana S. Scott, Outline of a mathematical theory of computation, in: Proceedings of the Fourth Annual Princeton Conference on Information Sciences and Systems (1970) 169–176. [pdf, pdf]

  • Dana S. Scott, Christopher Strachey, Toward a Mathematical Semantics for Computer Languages, Oxford University Computing Laboratory, Technical Monograph PRG-6 (1971) [pdf, pdf]

Textbook accounts:

  • Michael Sipser, Introduction to the Theory Of Computation, 3rd ed: Cengage Learning (2012) [ISBN:978-1-133-18779-0,pdf, pdf]

An account with focus on programming languages:

An account going from classical computation to quantum computation:

On computation in relation to physics (cf. computable physics):


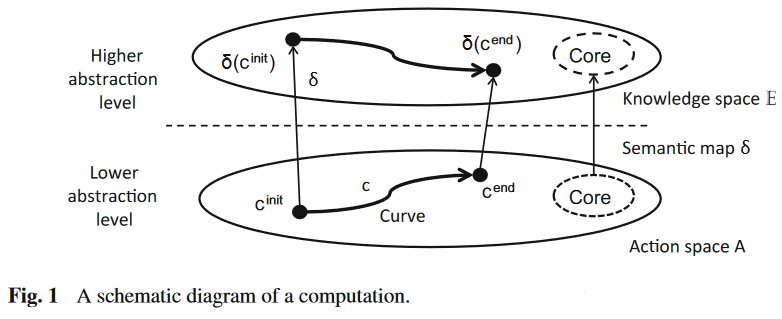
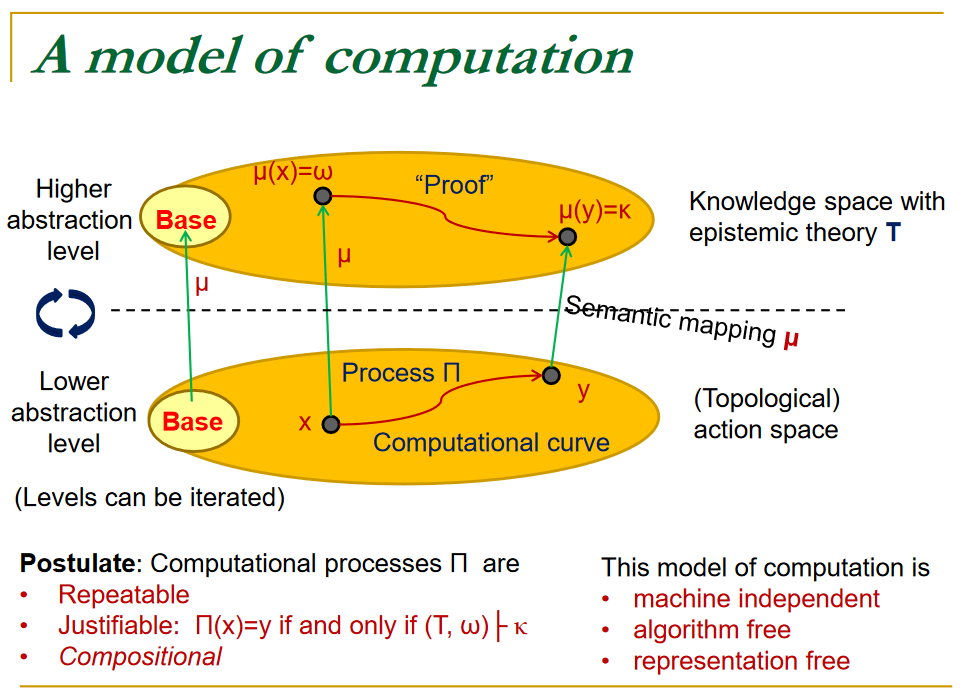
As path lifting

A conceptualization of computation as something at least close to path-lifting and/or as functors between path groupoids of topological spaces (a “semantical mapping” from an “action space” parameterizing the possible computing instructions to a “knowledge space” expressing their executions):

  • Jan van Leeuwen, The Philosophy of Computation, p. xix-xxx in: Proceedings of IIT.SRC 2015 – Student Research Conference Bratislava (2015) [full proceedings: pdf, web; article: pdf; slides: pdf]
(from van Leeuwen 2015)
(from van Leeuwen and Wiedermann 2017)

Related discussion for quantum computation, with quantum circuits regarded as paths:

Last revised on November 1, 2024 at 07:01:38. See the history of this page for a list of all contributions to it.

EditDiscussPrevious revisionChanges from previous revisionHistory (24 revisions) Cite Print Source