nLab spinning string
Context
String theory
Ingredients
Critical string models
Extended objects
Topological strings
Backgrounds
Phenomenology
Quantum field theory
Physics
physics, mathematical physics, philosophy of physics
Surveys, textbooks and lecture notes
theory (physics), model (physics)
experiment, measurement, computable physics
-
-
-
Axiomatizations
-
Tools
-
Structural phenomena
-
Types of quantum field thories
-
Contents
Idea
The spinning string is a variant of the string in direct analogy (but one worldvolume dimension higher) to how the spinning particle is a variant of the particle.
(Which means that “spinning” here is not in the sense of “rotating”, but in the sense of the kind of “intrinsic” spin as exhibited by fermion particles. A spinning string can rotate in addition to its intrinsic spin.)
And just as as the spinning particle automatically exhibits local worldline supersymmetry, the spinning string automatically exhibits local worldsheet supersymmetry. For that reason it is today almost exclusively known as the superstring .
In fact, the very notion of supersymmetry was realized (in parallel to its independent discovery in Russia) when people noticed that the spinning string sigma-model – also called the Neveu-Schwarz-Ramond model (NSR model) – automatically exhibits this extra graded symmetry.
When supplemented with an operation called the GSO projection, the second quantization of the spinning string – its effective target spacetime theory – also becomes a locally supersymmetric theory: spacetime supergravity.
There are other formulations of the superstring which are thought to be equivalent in some sense. Notably the Green-Schwarz superstring is a sigma-model which is not supersymmetric on the worldsheet but instead takes values in a genuine spacetime supermanifold.
Related concepts
manifest supersymmetry for brane sigma-models:
| manifest worldvolume supersymmetry | manifest target+worldvolume supersymmetry | manifest target space supersymmetry |
|---|---|---|
| NSR action functional | superembedding approach | Green-Schwarz action functional |
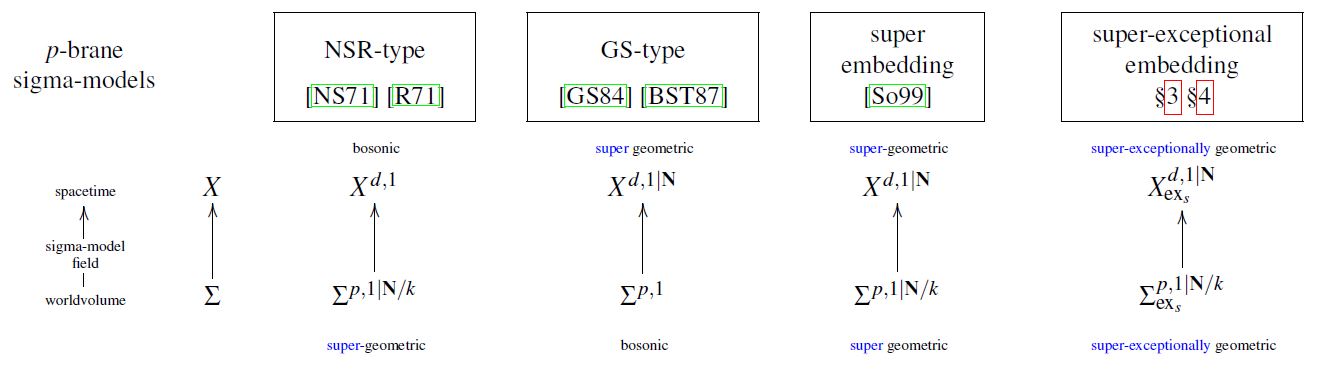
graphics grabbed from FSS19c
References
General
The original articles that formulated the NSR model:
-
André Neveu, John Schwarz, Factorizable dual model of pions, Nucl. Phys. B31, 86 (1971) (doi:10.1016/0550-3213(71)90448-2)
-
Pierre Ramond, Dual theory for Free Fermions, Phys Rev. D3 2415 (1971) (doi:10.1103/PhysRevD.3.2415)
(introducing the Dirac-Ramond operator)
-
Daniel Friedan, Emil Martinec, Stephen Shenker, Conformal invariance, supersymmetry and string theory, Nucl. Phys., B271 (1986) 93 (doi:10.1016/S0550-3213(86)80006-2)
Original articles that realize the local worldsheet supersymmetry of the spinning string (via the supersymmetric Polyakov action):
-
Stanley Deser, Bruno Zumino, A complete action for the spinning string, Physics Letters B 65 4 (1976) 369-373 [doi:10.1016/0370-2693(76)90245-8pdf]
-
Lars Brink, Paolo Di Vecchia, Paul Howe, A locally supersymmetric and reparametrization invariant action for the spinning string , Physics Letters B 65 Issue 5, 20 (1976) 471-474 [doi:10.1016/0370-2693(76)90445-7]
Further on the spinning string’s worldsheet theory as supergravity formulated in superspace:
- S. James Gates Jr., Liang Lu, Robert N. Oerter: Simplified spinning string superspace supergravity, Physics Letters B 218 1 (1989) 33-38 [doi:10.1016/0370-2693(89)90470-X, spire:263912]
Definition of the NSR string in RR-field backgrounds is subtle (in contrast to the classical Green-Schwarz superstring), discussion is in:
- David Berenstein, Robert Leigh, Superstring Perturbation Theory and Ramond-Ramond Backgrounds, Phys. Rev. D 60 106002 (1999) [arXiv:hep-th/9904104]
See also
- Nathan Benjamin, Ying-Hsuan Lin, Lessons from the Ramond sector (arXiv:2005.02394)
Relation to the Berkovits superstring:
- Nathan Berkovits, Manifest Spacetime Supersymmetry and the Superstring (arXiv:2106.04448)
GSO projection and spacetime supersymmetry
The GSO projection and the conjecture that this makes also the target space theory of the spinning string locally supersymmetric is due to
-
F. Gliozzi, Joël Scherk, D. I. Olive, Supergravity and its spinor dual model, Phys. Letters B65, 282 (1976)
-
F. Gliozzi, Joël Scherk, D. I. Olive, Supersymmetry, supergravity theories and the dual spinor model , Nucl. Phys, B122, 253 (1977)
The demonstration of this fact is due to
-
Supersymmetrical dual string theory , Nucl. Phys. B181 (1981) 502;
Supersymmetrical string theories , Phys. Lett. 109B (1982) 444.
Superconformal invariance of the spinning string was discussed in
- Paul Howe, Super Weyl transformations in two dimensions J. Phys. 12 (1979) 393.
A decent account is in
A review of the history of these developments is in
- John Schwarz, String theory origins of supersymmetry, Nucl. Phys. Proc. Suppl. 101 (2001) 54-61 (arXiv:hep-th/0011078)
An exposition of some technical aspects is in the wiki
Reviews and survays are also in any text on string theory. See the references there for more detail.
BRST description
Discussion of the BRST complex of the NSR string:
- José Figueroa-O'Farrill, Takashi Kimura, The BRST cohomology of the NSR string: vanishing and “-ghost’‘ theorems, Comm. Math. Phys. 124 1 (1989) 105-132. [euclid:cmp/1104179078]
Last revised on August 22, 2024 at 11:12:16. See the history of this page for a list of all contributions to it.