nLab Jackiw-Teitelboim gravity
Context
Gravity
Formalism
Definition
Spacetime configurations
Properties
Spacetimes
| black hole spacetimes | vanishing angular momentum | positive angular momentum |
|---|---|---|
| vanishing charge | Schwarzschild spacetime | Kerr spacetime |
| positive charge | Reissner-Nordstrom spacetime | Kerr-Newman spacetime |
Quantum theory
Contents
- Idea
- Properties
- Related concepts
- References
- General
- SYK-model in
- Random matrix theory in
- BFSS matrix model in
- Flat space limit
- D1-D3 brane intersections in
- Chord diagrams and weight systems in Physics
- In Chern-Simons theory
- For single trace operators in AdS/CFT duality
- In , JT-gravity/SYK-model
- In D/D-brane intersections
- As codes for holographic entanglement entropy
- For Dyson-Schwinger equations
- Other
- Application to near-extremal near-horizons
- Lift to string/M-theory
- In terms of weight systems on chord diagrams
Idea
JT-gravity (Teitelboim 83, Jackiw 85) is gravity in 1+1 dimensions with a dilaton.
Properties
Relation to near-extremal black holes
JT-gravity gives a good approximation to the AdS-factor in the near horizon geometry of near-extremal black holes in -dimensional spacetime (NSST18, MTV18).
Via the AdS/CFT-dual of JT-gravity (Almheiri-Polchinski 14) given by random matrix theory (Saad-Shenker-Stanford 19, Stanford-Witten 19) (or SYK model) this allows to compute genuine quantum gravity-aspects of near-extremal black holes, such as notable their microscopic black hole entropy. Computations are now under way…
Notice that near-extremal black holes have been observed in nature, by the Chandra telescope see eg here.
Related concepts
References
General
The theory is due to
-
Claudio Teitelboim, Gravitation and hamiltonian structure in two spacetime dimensions, Physics Letters B Volume 126, Issues 1–2, 23 June 1983, Pages 41-45 (doi:10.1016/0370-2693(83)90012-6
-
Roman Jackiw, Lower dimensional gravity, Nuclear Physics B
Volume 252, 1985, Pages 343-356 (doi:10.1016/0550-3213(85)90448-1)
Lecture notes:
- Gustavo J. Turiaci: Les Houches lectures on two-dimensional gravity and holography [arXiv:2412.09537]
See also:
- Wikipedia, Jackiw-Teitelboim gravity
Further development:
- Andreas Blommaert, Thomas G. Mertens, Henri Verschelde, Eigenbranes in Jackiw-Teitelboim gravity (arXiv:1911.11603)
Via twistors:
- Wolfgang Wieland, Twistor representation of Jackiw-Teitelboim gravity (arXiv:2003.13887)
On supergravity-versions of JT-gravity:
-
Gustavo J. Turiaci, Edward Witten, JT Supergravity and Matrix Models [arXiv:2305.19438]
-
Geoff Penington, Edward Witten: Algebras and states in super-JT gravity [arXiv:2412.15549]
SYK-model in
Discussion of the SYK-model as the AdS/CFT dual of JT-gravity in nearly AdS2/CFT1 and AdS-CFT in condensed matter physics:
Original articles:
-
Juan Maldacena, Douglas Stanford, Comments on the Sachdev-Ye-Kitaev model, Phys. Rev. D 94, 106002 (2016)(arXiv:1604.07818)
-
Subir Sachdev, Holographic metals and the fractionalized Fermi liquid, Phys. Rev. Lett. 105:151602, 2010 (arXiv:1006.3794)
Review:
-
Gábor Sárosi, holography and the SYK model, Proceedings of Science 323 (arXiv:1711.08482, doi:10.22323/1.323.0001)
-
Juan Maldacena, Toy models for black holes II, talk at PiTP 2018 From QBits to spacetime (recording)
-
Dmitrii A. Trunin, Pedagogical introduction to SYK model and 2D Dilaton Gravity (arXiv:2002.12187)
Relation to black holes in terms of Majorana dimer states:
- Ioanna Kourkoulou, Juan Maldacena, Pure states in the SYK model and nearly- gravity (arXiv:1707.02325)
Relation to black holes in string theory and random matrix theory:
-
Jordan S. Cotler, Guy Gur-Ari, Masanori Hanada, Joseph Polchinski, Phil Saad, Stephen Shenker, Douglas Stanford, Alexandre Streicher, Masaki Tezuka, Black Holes and Random Matrices, JHEP 1705:118, 2017 (arXiv:1611.04650)
-
Tomoki Nosaka, Tokiro Numasawa, Quantum Chaos, Thermodynamics and Black Hole Microstates in the mass deformed SYK model (arXiv:1912.12302)
On non-perturbative effects and resurgence:
- Paolo Gregori, Ricardo Schiappa, From Minimal Strings towards Jackiw-Teitelboim Gravity: On their Resurgence, Resonance, and Black Holes (arXiv:2108.11409)
See also
-
Yuri D. Lensky, Xiao-Liang Qi, Pengfei Zhang, Size of bulk fermions in the SYK model (arXiv:2002.01961)
-
Xiao-Liang Qi, Pengfei Zhang, The Coupled SYK model at Finite Temperature (arXiv:2003.03916)
-
Akash Goel, Herman Verlinde, Towards a String Dual of SYK (arXiv:2103.03187)
-
Tarek Anous, Felix M. Haehl, The quantum -spin glass model: A user manual for holographers (arXiv:2106.03838)
Discussion of small N corrections via a lattice QFT-Ansatz on the AdS side:
- Richard C. Brower, Cameron V. Cogburn, A. Liam Fitzpatrick, Dean Howarth, Chung-I Tan, Lattice Setup for Quantum Field Theory in (arXiv:1912.07606)
See also:
- Gregory J. Galloway, Melanie Graf, Eric Ling, A conformal infinity approach to asymptotically spacetimes (arXiv:2003.00093)
Random matrix theory in
On Jackiw-Teitelboim gravity dual to random matrix theory (via AdS2/CFT1 and topological recursion):
-
Ahmed Almheiri, Joseph Polchinski, Models of Backreaction and Holography, J. High Energ. Phys. 2015 14 (2015) [arXiv:1402.6334]
-
Phil Saad, Stephen Shenker, Douglas Stanford, JT gravity as a matrix integral (arXiv:1903.11115)
-
Douglas Stanford, Edward Witten, JT Gravity and the Ensembles of Random Matrix Theory (arXiv:1907.03363)
-
Ping Gao, Daniel L. Jafferis, David K. Kolchmeyer, An effective matrix model for dynamical end of the world branes in Jackiw-Teitelboim gravity, J. High Energ. Phys. 2022 38 (2022) [doi:10.1007/JHEP01(2022)038, arXiv:2104.01184]
BFSS matrix model in
On AdS2/CFT1 with the BFSS matrix model on the CFT side and black hole-like solutions in type IIA supergravity on the AdS side:
- Juan Maldacena, Alexey Milekhin, To gauge or not to gauge?, JHEP 04 (2018) 084 (arxiv:1802.00428)
and on its analog of holographic entanglement entropy:
- Tarek Anous, Joanna L. Karczmarek, Eric Mintun, Mark Van Raamsdonk, Benson Way, Areas and entropies in BFSS/gravity duality (arXiv:1911.11145)
See also
- Takeshi Morita, Hiroki Yoshida, A Critical Dimension in One-dimensional Large-N Reduced Models (arXiv:2001.02109)
Flat space limit
The SYK model in flat space holography:
- Hamid Afshar, Hernan Gonzalez, Daniel Grumiller, Dmitri Vassilevich, Flat space holography and complex SYK, Phys. Rev. D 101, 086024 (arXiv:1911.05739, doi:10.1103/PhysRevD.101.086024)
D1-D3 brane intersections in
On D1-D3 brane intersections in AdS2/CFT1:
- Giuseppe Dibitetto, Yolanda Lozano, Nicolò Petri, Anayeli Ramirez, Holographic Description of M-branes via (arXiv:1912.09932)
Via T-duality from D6-D8 brane intersections:
- Yolanda Lozano, Carlos Nunez, Anayeli Ramirez, Stefano Speziali, New backgrounds and Conformal Quantum Mechanics (arXiv:2011.00005)
Chord diagrams and weight systems in Physics
The following is a list of references that involve (weight systems on) chord diagrams/Jacobi diagrams in physics:
-
In quantum many body models for for holographic brane/bulk correspondence:
For a unifying perspective (via Hypothesis H) and further pointers, see:
-
Hisham Sati, Urs Schreiber, Differential Cohomotopy implies intersecting brane observables, Adv. Theor. Math. Phys. 26 4 (2022) [doi:10.4310/ATMP.2022.v26.n4.a4arXiv:1912.10425]
-
David Corfield, Hisham Sati, Urs Schreiber: Fundamental weight systems are quantum states Lett. Math. Phys. 113 112 (2023) [arXiv:2105.02871, doi:10.1007/s11005-023-01725-4]
-
Carlo Collari, A note on weight systems which are quantum states, Can. Math. Bull. 66 4 (2023) [doi:10.4153/S0008439523000206, arXiv:2210.05399]
Review:
- Carlo Collari, Weight systems which are quantum states, talk at QFT and Cobordism, CQTS (Mar 2023) web, pdf
In Chern-Simons theory
Since weight systems are the associated graded of Vassiliev invariants, and since Vassiliev invariants are knot invariants arising as certain correlators/Feynman amplitudes of Chern-Simons theory in the presence of Wilson lines, there is a close relation between weight systems and quantum Chern-Simons theory.
Historically this is the original application of chord diagrams/Jacobi diagrams and their weight systems, see also at graph complex and Kontsevich integral.
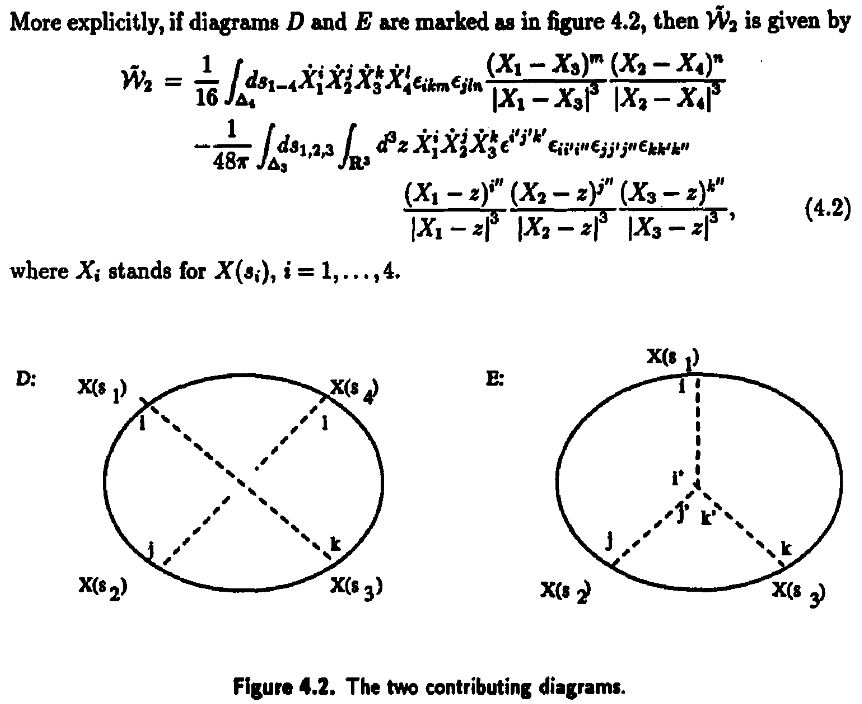
-
Dror Bar-Natan, Perturbative aspects of the Chern-Simons topological quantum field theory, thesis 1991 (spire:323500, proquest:303979053, BarNatanPerturbativeCS91.pdf)
-
Maxim Kontsevich, Vassiliev’s knot invariants, Advances in Soviet Mathematics, Volume 16, Part 2, 1993 (pdf)
-
Daniel Altschuler, Laurent Freidel, Vassiliev knot invariants and Chern-Simons perturbation theory to all orders, Commun. Math. Phys. 187 (1997) 261-287 (arxiv:q-alg/9603010)
-
Alberto Cattaneo, Paolo Cotta-Ramusino, Riccardo Longoni, Configuration spaces and Vassiliev classes in any dimension, Algebr. Geom. Topol. 2 (2002) 949-1000 (arXiv:math/9910139)
-
Alberto Cattaneo, Paolo Cotta-Ramusino, Riccardo Longoni, Algebraic structures on graph cohomology, Journal of Knot Theory and Its Ramifications, Vol. 14, No. 5 (2005) 627-640 (arXiv:math/0307218)
Reviewed in:
- Ismar Volić, Section 4 of: Configuration space integrals and the topology of knot and link spaces, Morfismos, Vol 17, no 2, 2013 (arxiv:1310.7224)
Applied to Gopakumar-Vafa duality:
- Dave Auckly, Sergiy Koshkin, Introduction to the Gopakumar-Vafa Large Duality, Geom. Topol. Monogr. 8 (2006) 195-456 (arXiv:0701568)
See also
-
Marcos Mariño, Chern-Simons theory, matrix integrals, and perturbative three-manifold invariants, Commun. Math. Phys. 253 (2004) 25-49 (arXiv:hep-th/0207096)
-
Stavros Garoufalidis, Marcos Mariño, On Chern-Simons matrix models (pdf, pdf)
For single trace operators in AdS/CFT duality
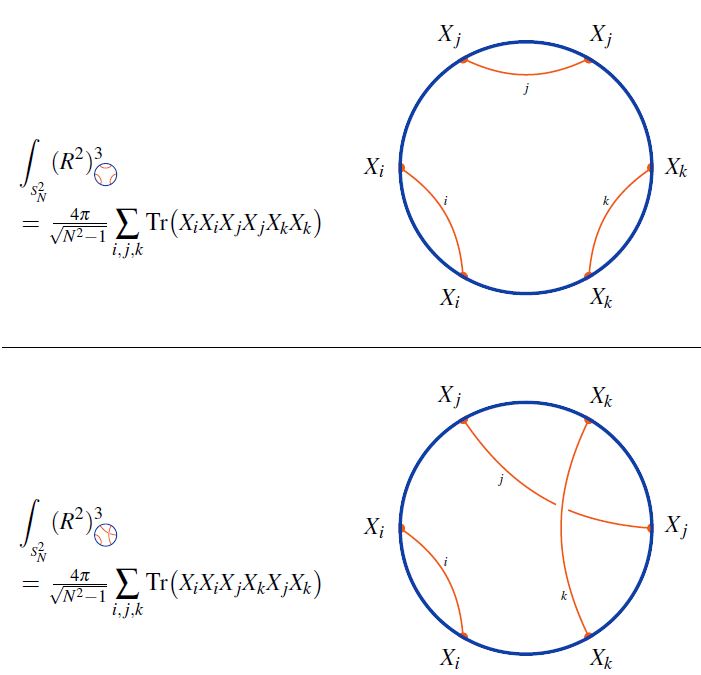
Interpretation of Lie algebra weight systems on chord diagrams as certain single trace operators, in particular in application to black hole thermodynamics
- Micha Berkooz, Prithvi Narayan, Joan Simón, Section 2.1 of Chord diagrams, exact correlators in spin glasses and black hole bulk reconstruction, JHEP 08 (2018) 192 (arxiv:1806.04380)
In , JT-gravity/SYK-model
Discussion of (Lie algebra-)weight systems on chord diagrams as SYK model single trace operators:
-
Antonio M. García-García, Yiyang Jia, Jacobus J. M. Verbaarschot, Exact moments of the Sachdev-Ye-Kitaev model up to order , JHEP 04 (2018) 146 (arXiv:1801.02696)
-
Yiyang Jia, Jacobus J. M. Verbaarschot, Section 4 of: Large expansion of the moments and free energy of Sachdev-Ye-Kitaev model, and the enumeration of intersection graphs, JHEP 11 (2018) 031 (arXiv:1806.03271)
-
Micha Berkooz, Prithvi Narayan, Joan Simón, Chord diagrams, exact correlators in spin glasses and black hole bulk reconstruction, JHEP 08 (2018) 192 (arxiv:1806.04380)
following:
- László Erdős, Dominik Schröder, Phase Transition in the Density of States of Quantum Spin Glasses, D. Math Phys Anal Geom (2014) 17: 9164 (arXiv:1407.1552)
which in turn follows
- Philippe Flajolet, Marc Noy, Analytic Combinatorics of Chord Diagrams, pages 191–201 in Daniel Krob, Alexander A. Mikhalev,and Alexander V. Mikhalev, (eds.), Formal Power Series and Algebraic Combinatorics, Springer 2000 (doi:10.1007/978-3-662-04166-6_17)

With emphasis on the holographic content:
-
Micha Berkooz, Mikhail Isachenkov, Vladimir Narovlansky, Genis Torrents, Section 5 of: Towards a full solution of the large double-scaled SYK model, JHEP 03 (2019) 079 (arxiv:1811.02584)
-
Vladimir Narovlansky, Slide 23 (of 28) of: Towards a Solution of Large Double-Scaled SYK, 2019 (pdf)
-
Micha Berkooz, Mikhail Isachenkov, Prithvi Narayan, Vladimir Narovlansky, Quantum groups, non-commutative , and chords in the double-scaled SYK model [arXiv:2212.13668]
-
Herman Verlinde, Double-scaled SYK, Chords and de Sitter Gravity [arXiv:2402.00635]
-
Micha Berkooz, Nadav Brukner, Yiyang Jia, Ohad Mamroud, A Path Integral for Chord Diagrams and Chaotic-Integrable Transitions in Double Scaled SYK [arXiv:2403.05980]
and specifically in relation, under AdS2/CFT1, to Jackiw-Teitelboim gravity:
-
Andreas Blommaert, Thomas Mertens, Henri Verschelde, The Schwarzian Theory - A Wilson Line Perspective, JHEP 1812 (2018) 022 (arXiv:1806.07765)
-
Andreas Blommaert, Thomas Mertens, Henri Verschelde, Fine Structure of Jackiw-Teitelboim Quantum Gravity, JHEP 1909 (2019) 066 (arXiv:1812.00918)
-
Henry W. Lin, The bulk Hilbert space of double scaled SYK, J. High Energ. Phys. 2022 60 (2022) arXiv:2208.07032, doi:10.1007/JHEP11(2022)060
-
Henry W. Lin, Douglas Stanford, A symmetry algebra in double-scaled SYK arXiv:2307.15725
-
Micha Berkooz, Ohad Mamroud: A Cordial Introduction to Double Scaled SYK [arXiv:2407.09396]
-
Adel A. Rahman, Leonard Susskind: -Chords, Wee-Chords, and de Sitter Space [arXiv:2407.12988]
In D/D-brane intersections
Discussion of weight systems on chord diagrams as single trace observables for the non-abelian DBI action on the fuzzy funnel/fuzzy sphere non-commutative geometry of Dp-D(p+2)-brane intersections (hence Yang-Mills monopoles):
-
Sanyaje Ramgoolam, Bill Spence, S. Thomas, Section 3.2 of: Resolving brane collapse with corrections in non-Abelian DBI, Nucl. Phys. B703 (2004) 236-276 (arxiv:hep-th/0405256)
-
Simon McNamara, Constantinos Papageorgakis, Sanyaje Ramgoolam, Bill Spence, Appendix A of: Finite effects on the collapse of fuzzy spheres, JHEP 0605:060, 2006 (arxiv:hep-th/0512145)
-
Simon McNamara, Section 4 of: Twistor Inspired Methods in Perturbative FieldTheory and Fuzzy Funnels, 2006 (spire:1351861, pdf, pdf)
-
Constantinos Papageorgakis, p. 161-162 of: On matrix D-brane dynamics and fuzzy spheres, 2006 (pdf)
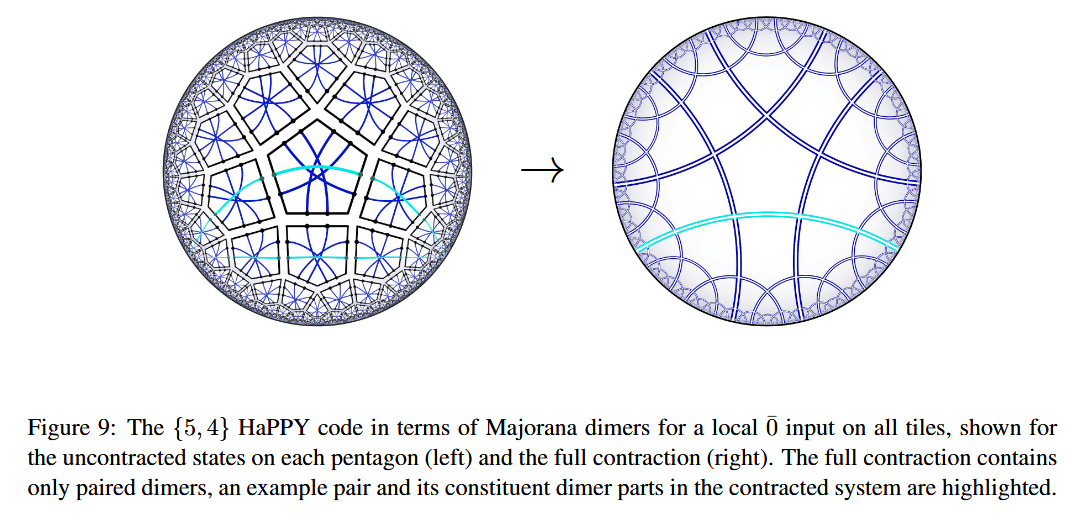
As codes for holographic entanglement entropy
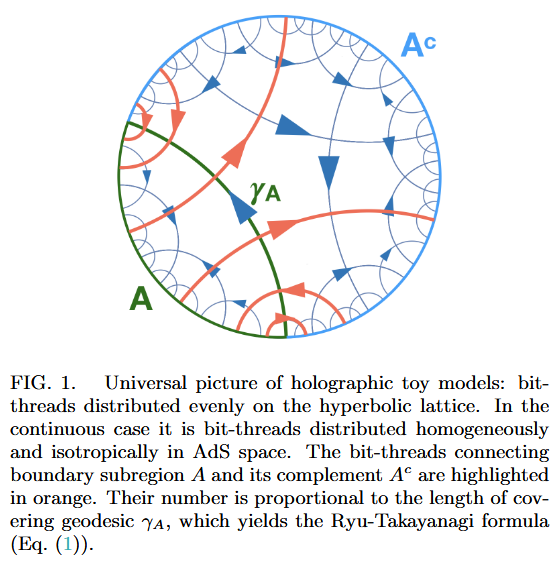
Chord diagrams encoding Majorana dimer codes and other quantum error correcting codes via tensor networks exhibiting holographic entanglement entropy:
-
Alexander Jahn, Marek Gluza, Fernando Pastawski, Jens Eisert, Majorana dimers and holographic quantum error-correcting code, Phys. Rev. Research 1, 033079 (2019) (arXiv:1905.03268)
-
Han Yan, Geodesic string condensation from symmetric tensor gauge theory: a unifying framework of holographic toy models, Phys. Rev. B 102, 161119 (2020) (arXiv:1911.01007)
For Dyson-Schwinger equations
Discussion of round chord diagrams organizing Dyson-Schwinger equations:
-
Nicolas Marie, Karen Yeats, A chord diagram expansion coming from some Dyson-Schwinger equations, Communications in Number Theory and Physics, 7(2):251291, 2013 (arXiv:1210.5457)
-
Markus Hihn, Karen Yeats, Generalized chord diagram expansions of Dyson-Schwinger equations, Ann. Inst. Henri Poincar Comb. Phys. Interact. 6 no 4:573-605 (arXiv:1602.02550)
-
Paul-Hermann Balduf, Amelia Cantwell, Kurusch Ebrahimi-Fard, Lukas Nabergall, Nicholas Olson-Harris, Karen Yeats, Tubings, chord diagrams, and Dyson-Schwinger equations [arXiv:2302.02019]
Review in:
- Ali Assem Mahmoud, Section 3 of: On the Enumerative Structures in Quantum Field Theory (arXiv:2008.11661)
Other
Appearance of horizontal chord diagrams in discussion of neutrino interactions in supernovae:
- Duff Neill, Hanqing Liu, Joshua Martin, Alessandro Roggero: Scattering Neutrinos, Spin Models, and Permutations [arXiv:2406.18677]
Application to near-extremal near-horizons
Application to near horizon geometry of near-extremal black holes:
-
Pranjal Nayak, Ashish Shukla, Ronak M Soni, Sandip Trivedi, V. Vishal, On the Dynamics of Near-Extremal Black Holes, J. High Energ. Phys. 2018 48 (2018) [doi:10.1007/JHEP09(2018)048, arXiv:1802.09547]
-
Upamanyu Moitra, Sandip Trivedi, V. Vishal, Near-Extremal Near-Horizons (arXiv:1808.08239)
Lift to string/M-theory
Realization of JT-gravity as Kaluza-Klein reduction of D=6 supergravity on the worldvolume of D1-D5 brane bound states or M2-M5 brane bound states:
-
Yue-Zhou Li, Shou-Long Li, H. Lu, Exact Embeddings of JT Gravity in Strings and M-theory, Eur. Phys. J. C (2018) 78: 791 (arXiv:1804.09742)
-
Iosif Bena, Pierre Heidmann, David Turton, Holography: Mind the Cap, JHEP 1812 (2018) 028 (arXiv:1806.02834)
-
Giuseppe Dibitetto, Nicolò Petri, solutions and their massive IIA origin, JHEP 05 (2019) 107 (arXiv:1811.11572)
-
Junho Hong, Niall Macpherson, Leopoldo A. Pando Zayas, Aspects of classification in M-theory: Solutions with mesonic and baryonic charges, JHEP 11 (2019) 127 (arXiv:1908.08518)
In terms of weight systems on chord diagrams
Discussion of (Lie algebra-)weight systems on chord diagrams encoding JT gravity observables
(for more see at weight systems on chord diagrams in physics):
-
Andreas Blommaert, Thomas Mertens, Henri Verschelde, The Schwarzian Theory - A Wilson Line Perspective, JHEP 1812 (2018) 022 (arXiv:1806.07765)
-
Andreas Blommaert, Thomas Mertens, Henri Verschelde, Fine Structure of Jackiw-Teitelboim Quantum Gravity, JHEP 1909 (2019) 066 (arXiv:1812.00918)
and similarly, under AdS2/CFT1, as correlators in the SYK model:
-
Antonio M. García-García, Yiyang Jia, Jacobus J. M. Verbaarschot, Exact moments of the Sachdev-Ye-Kitaev model up to order , JHEP 04 (2018) 146 (arXiv:1801.02696)
-
Micha Berkooz, Prithvi Narayan, Joan Simón, Chord diagrams, exact correlators in spin glasses and black hole bulk reconstruction, JHEP 08 (2018) 192 (arxiv:1806.04380)
following:
- László Erdős, Dominik Schröder, Phase Transition in the Density of States of Quantum Spin Glasses, D. Math Phys Anal Geom (2014) 17: 9164 (arXiv:1407.1552)
which in turn follows
- Philippe Flajolet, Marc Noy, Analytic Combinatorics of Chord Diagrams, pages 191–201 in Daniel Krob, Alexander A. Mikhalev,and Alexander V. Mikhalev, (eds.), Formal Power Series and Algebraic Combinatorics, Springer 2000 (doi:10.1007/978-3-662-04166-6_17)

With emphasis on holographic content:
-
Micha Berkooz, Mikhail Isachenkov, Vladimir Narovlansky, Genis Torrents, Section 5 of: Towards a full solution of the large double-scaled SYK model, JHEP 03 (2019) 079 (arxiv:1811.02584)
-
Vladimir Narovlansky, Slide 23 (of 28) of: Towards a Solution of Large Double-Scaled SYK, 2019 (pdf)
Last revised on December 24, 2024 at 09:14:57. See the history of this page for a list of all contributions to it.