Schreiber Super topological T-Duality

$\,$

$\;$ Urs Schreiber (CAS Prague & I-Math Zurich)

$\;$ Super Topological T-Duality (recording)

$\;$ talk at Conf. on Duality in Homotopy theory

$\;$ April 3-7, 2017, Regensburg

$\,$

Abstract. Twisted cohomology is maps in the tangent homotopy theory of parameterized spectra. Its rationalization has a Quillen-Sullivan-type model in terms of unbounded L-∞ algebras (SS 17). Interesting examples appear by constructing iterated maximal higher central extensions of super L-∞ algebras, invariant with respect to automorphisms modulo R-symmetries – a super-equivariant version of the Whitehead tower. Applied to the superpoint, this process turns out to discover all the twisted cohomology seen in string/M-theory (FSS 13, HS 17), rationally, in particular twisted topological K-theory with 5-brane correction and with supersymmetric Chern-forms on 10d-superspace (FSS 16a). Passage to cyclic L-∞ cohomology reflects double dimensional reduction of super p-branes. Applied to twisted K-theory on 10d superspace this yields two L-∞ cocycles on 9d superspace which both classify the tangent complex of super T-folds. There appears a super L-∞ equivalence between them exhibiting supersymmetric topological T-duality, rationally (FSS 16b).

These rational phenomena indicate that integrally the super-equivariant Whitehead tower of the superpoint is a mechanism for discovering interesting twisted super-differential cohomology theories (dcct). We close with an outlook on the relevant constructions.

Lecture notes with more details are here:

• geometry of physics – fundamental super p-branes.

Related talks

• Introduction to Higher Supergeometry (talk at Higher structures in M-theory, 2018)

• Super p-Brane Theory emerging from Super Homotopy-Theory (talk at StringMath 2017)

• Super topological T-Duality (talk at Duality in Homotopy theory 2017)

• Super Lie n-algebra of Super p-branes (talk at TQFT Seminar Lisbon, 2017 alongside Iberian Strings 2017)

• Structured Homotopy Theory and String Theory

$\,$

$\,$

$\,$

Super $L_\infty$

$\,$

For the bulk of this talk, the homotopy theory we consider

is that of super L-∞ algebras:

$\,$

Definition

A super L-∞ algebra

is an L-∞ algebra internal to super vector spaces.

$\,$

Those of finite type are equivalently

the formal duals

of augmented dg-algebra structures

on free $(\mathbb{Z} \times (\mathbb{Z}/2))$-bi-graded commutative algebras

over chain complexes of super vector spaces,

namely their Chevalley-Eilenberg algebras:

$\,$

$$\array{ CE &\colon& s L_\infty^{fin} &\phantom{AA}\hookrightarrow \phantom{AA}& (dgAlg_{\mathbb{R}})_{/\mathbb{R}}^{op} \\ && (\, \mathfrak{g}\,, \, [-], [-,-], [-,-,-] ,\cdots \,) &\phantom{AA}\mapsto \phantom{AA}& \left( \, \wedge^\bullet \mathfrak{g}^\ast ,\, d_{\mathfrak{g}} \coloneqq [-]^\ast + [-,-]^\ast + [-,-,-]^\ast + \cdots \, \right) } \,.$$

$\,$

Proposition

(Pridham 10, prop. 4.36)

There is the structure of a category of fibrant objects on $sL_\infty Alg_{\mathbb{R}}$ whose

• fibrations are the surjections

• weak equivalences are the quasi-isomorphisms

on the underlying chain complexes $(\,\mathfrak{g}\,,\, \partial = [-]\,)$.

$\,$

We will keep using the following fact:

$\,$

Proposition

(FSS 13, theorem 3.8)

Write

$$B^{p+1}\mathbb{R}$$

for the line Lie (p+2)-algebra, given by

$$CE(B^{p+1}\mathbb{R}) \;=\; \left( Sym \underset{\text{single generator} \atop \text{in deg.} \, (p+2,even)}{\underbrace{\langle c_{p+2} \rangle}} \;,\; d = 0 \right) \,.$$

A $(p+2)$-cocycle on an $L_\infty$-algebra is equivalently a super $L_\infty$-homomorphism

$$\mu_{p+2} \;\colon\; \mathfrak{g} \longrightarrow B^{p+1}\mathbb{R} \,.$$

The homotopy fiber of this map

$$\array{ \widehat{\mathfrak{g}} \\ {}^{\mathllap{hofib(\mu_{p+2})}}\downarrow \\ \mathfrak{g} &\underset{\mu_{p+2}}{\longrightarrow}& B^{p+1}\mathbb{R} }$$

is given, up to equivalence, by adjoining to $CE(\mathfrak{g})$ a single generator $b_{p+1}$

forced to be a potential for $\mu_{p+2}$:

$$CE(\widehat{\mathfrak{g}}) \;\simeq\; CE(\mathfrak{g})[b_{p+1}]/(d b_{p+1} = \mu_{p+2}) \,.$$

$\,$

Example

$\,$

The homotopy fiber of a 2-cocycle

is the classical central extension

that it classifies.

Hence:

$\;\;$ The higher central extensions

$\;\;$ classified by higher cocycles

$\;\;$ are their homotopy fibers.

$\,$

Proposition

($L_\infty$-Algebra and Rational homotopy theory)

L-∞ algebras capture a broad range of aspects

of rational homotopy theory:

$\,$

1) The rational homotopy theory of simply connected topological spaces embeds

as the homotopy theory of connected $L_\infty$-algebras (Quillen 69, Hinich 98):

$$\mathfrak{l} \;\colon\; Spaces_{\mathbb{R},\geq 2 } \overset{\simeq}{\longrightarrow} L_\infty Alg_{\mathbb{R},\geq 1} \,.$$

$\,$

2) The rational stable homotopy theory of rational spectra embeds

as the abelian $L_\infty$-algebras: the plain chain complexes (Schwede-Shipley 03):

$$\mathfrak{l} \;\colon\; Spectra_{\mathbb{R}} \overset{\simeq}{\longrightarrow} L_\infty Alg_{\mathbb{R}, D = [-]} \simeq Ch_\bullet(\mathbb{R})$$

$\,$

3) The parameterized homotopy theory, of rational parameterized spectra

over some connected rational space $X$

embeds into the slice over $\mathfrak{l}(X)$

on those whose augmentation ideal is a chain complex $V$ (Schlegel-Schreiber):

$$\mathfrak{l} \;\colon\; (Spectra_{/X})_{\mathbb{R}} \overset{\simeq}{\longrightarrow} L_\infty Alg_{/\mathfrak{l}(X), ker \epsilon \in \mathrm{Ch}_\bullet(\mathbb{R})} = \left\{ \array{ V &\longrightarrow& \mathfrak{l}(X) \ltimes V \\ && \downarrow \\ && \mathfrak{l}(X) } \right\} \,.$$

4) Hence super L-∞ algebras generalize all this

to the rationalization of “super-homotopy theory”.

We say more about this below.

$\,$

Remark

These parameterized spectra

are the coefficients for twisted generalized cohomology.

For example for ring spectra $E$ then

there is a spectrum $E/GL_1(E)$ parameterized over $B GL_1(E)$

$$\array{ E &\longrightarrow& E/GL_1(E) \\ && \downarrow \\ && B GL_1(E) }$$

such that maps $\tau \colon X \to B GL_1(E)$ are twists

and the $\tau$-twisted $E$-cohomology is

$$E^{\bullet + \tau}(X) = \left\{ \array{ X && \longrightarrow && E/GL_1(E) \\ & {}_{\mathllap{\tau}}\searrow && \swarrow \\ && B GL_1(E) } \right\}$$

See at tangent (∞,1)-topos for more on this.

$\,$

Example

(the single source of all following examples)

The simplest non-trivial super L-∞ algebras

are the superpoints $\mathbb{R}^{0 \vert q}$

defined by

$$CE(\mathbb{R}^{0 \vert 1}) = \left( Sym \left( \underoverset{i = 1}{q}{\oplus} \langle \underset{deg = (1,odd)}{\underbrace{\mathbf{d}\theta_i}} \rangle \right) , d = 0 \right)$$

$\,$

In the following we do nothing but analyzing the

consecutive higher invariant central extensions

of the superpoint.

$\,$

Spacetime

Proposition

The maximal central extension of the superpoint $\mathbb{R}^{0\vert 1}$

is the super Lie algebra $\mathbb{R}^{0,1\vert 1}$

called the $N = 1$ super-worldline of the superparticle:

• whose even part is spanned by one generator $H$

• whose odd part is spanned by one generator $Q$

• the only non-trivial bracket is

  $$[Q, Q] = H$$

Next, the maximal central extension of $\mathbb{R}^{0\vert 2}$

is the $d = 3$, $N = 1$ super Minkowski spacetime

$$\array{ \mathbb{R}^{2,1\vert \mathbf{2}} \\ \downarrow \\ \mathbb{R}^{0\vert 2} } \,.$$

• whose even part is $\mathbb{R}^3$, spanned by generators $P_0, P_1, P_2$

• whose odd part is $\mathbb{R}^2$, regarded as

  the Majorana spinor representation $\mathbf{2}$

  of $Spin(2,1) \simeq SL(2,\mathbb{R})$

• the only non-trivial bracket is the spinor bilinear pairing

  $$[Q_\alpha, Q'_\beta] = C_{\alpha \alpha'} \Gamma_a{}^{\alpha'}{}_\beta \,P^a$$

where $C_{\alpha \beta}$ is the charge conjugation matrix

(and we use Einstein summation convention and leaves sums over repeated indices implicit).

$\,$

Proof

(skip proof)

Recall that

$d$-dimensional central extensions of super Lie algebras $\mathfrak{g}$

are classified by 2-cocycles.

These are super-skew symmetric bilinear maps

$$\mu_2 \;\colon\; \mathfrak{g} \wedge\mathfrak{g} \longrightarrow \mathbb{R}^d$$

satisfying a cocycle condition.

The extension $\widehat{\mathfrak{g}}$ that this classifies

has underlying super vector space

the direct sum

$$\widehat{\mathfrak{g}} \coloneqq \mathfrak{g} \oplus \mathbb{R}^d$$

an the new super Lie bracket is given

on pairs $(x,c) \in \mathfrak{g} \oplus \mathbb{R}^d$

by

$$[\; (x_1,c_1), (x_2,c_2)\;]_{\mu_2} \;=\; (\, [x_1,x_2]\,,\, \mu_2(c_1,c_2) \,) \,.$$

The condition that the new bracket $[-,-]_{\mu_2}$ satisfies the super Jacobi identity

is equivalent to the cocycle condition on $\mu_2$.

Now

in the case that $\mathfrak{g} = \mathbb{R}^{0\vert q}$,

then the cocycle condition is trivial

and a 2-cocycle is just a symmetric bilinear form

on the $q$ fermionic dimensions.

So

in the case $\mathfrak{g} = \mathbb{R}^{0\vert 1}$

there is a unique such, up to scale, namely

$$\mu_2(a Q,b Q) = a b P \,.$$

But

in the case $\mathfrak{g} = \mathbb{R}^{0\vert 2}$

there is a 3-dimensional space of 2-cocycles, namely

$$\mu_2 \left( \left( \array{ Q_1 \\ Q_2 }\right), \left( \array{ Q'_1 \\ Q'_2 } \right) \right) = \left\{ \array{ Q_1 Q'_1, & \tfrac{1}{2}\left( Q_1 Q'_2 + Q_2 Q'_1 \right), \\ & Q_2 Q'_2 } \right.$$

If this is identified with the three coordinates

of 3d Minkowski spacetime

$$\mathbb{R}^{2,1} \;\simeq\; \left( \array{ t + x & y \\ & t - x } \right)$$

then the pairing is the claimed one

(see at supersymmetry – in dimensions 3,4,6,10).

$\,$

This phenomenon continues:

$\,$

Definition

Given a super Lie algebra $\mathfrak{g}$, write

1. $\mathfrak{aut}_{even}(\mathfrak{g})$ for the even part of its super Lie algebra of even derivations;

2. $\mathfrak{int}(\mathfrak{g}) \coloneqq stab_{ \mathfrak{aut}_{even}(\mathfrak{g}) }(\mathfrak{g}_{even})$ for the stabilizer of the even part

   – called the infinitesimal R-symmetries.

3. $\mathfrak{ext}(\mathfrak{g}) = \mathfrak{aut}_{even}(\mathfrak{g})/\mathfrak{int}(\mathfrak{g})$ the external automorphisms, making a short exact sequence

   $$0 \to \mathrm{int}(\mathfrak{g}) \hookrightarrow \mathfrak{aut}_{even}(\mathfrak{g}) \longrightarrow \mathfrak{ext}(\mathfrak{g}) \to 0$$

If that sequence splits and if $\mathfrak{aut}_{even}(\mathfrak{g})$ is reductive

then we consider the semisimple direct summand

$$\mathrm{ext}_{ssimple}(\mathfrak{g}) \hookrightarrow \mathfrak{ext}(\mathfrak{g}) \hookrightarrow \mathfrak{aut}_{even}(\mathfrak{g}) \,.$$

$\,$

Theorem

(Huerta-Schreiber 17)

The diagram of super Lie algebras shown on the right

is obtained by consecutively forming

maximal central extensions

invariant with respect to

the semisimple external automorphisms (def. )

at the given stage.

Here $\mathbb{R}^{d-1,1\vert \mathbf{N}}$

is the $d$-dimensional, $\mathbf{N}$-supersymmetric

super-translation algebra (see at geometry of physics – supersymmetry).

$$CE(\mathbb{R}^{d-1,1\vert \mathbf{N}}) = \left( \array{ Sym\left( \underset{deg = (1,even)}{\underbrace{\langle e^a \rangle_{a = 0}^{d-1}}} \oplus \underset{def = (1,odd)}{\underbrace{\langle \psi^\alpha \rangle_{\alpha = 1}^N}} \right) , \\ { d \psi^\alpha = 0 \,, d e^a = \underset{ \text{spinor-to-vector-pairing in real spin rep}\, \mathbf{N} }{\underbrace{\overline{\psi} \wedge \Gamma^a \psi = (C \Gamma^a)_{\alpha \beta} \psi^\alpha \wedge \psi^\beta}} } } \right)$$

And these semisimple subgroups are in each case

the spin group covers $Spin(d-1,1)$

of the proper orthochronous Lorentz groups $SO^+(d-1,1)$.

$\,$

Conclusion:

Just from studying iterated invariant central extensions

of super Lie algebras,

starting with the superpoint,

we (re-)discover

1. Lorentzian geometry,

2. spin geometry.

3. super spacetimes.

$\,$

$\,$

May we extend further?

$\,$

Branes

Proposition

(Achúcarro-Evans-Townsend-Wiltshire 87, Brandt 12-13)

The space of maximal invariant indecomposable cocycles

1. on 10d super Minkowski spacetime $\mathbb{R}^{9,1 \vert \mathbf{N}}$

   is spanned by a single 3-cocycle

   $$\mu_{F1} = \left(\overline{\psi} \wedge \Gamma_a \psi\right) \wedge e^a$$

2. on 11d super Minkowski spacetime $\mathbb{R}^{10,1\vert\mathbf{32}}$ is spanned by the 4-cocycle

   $$\mu_{M2} = i \left(\overline{\psi} \wedge \Gamma_{a b} \psi \right) \wedge e^a \wedge e^b$$

This classification is also known as

the old brane scan.

$\,$

Definition

$\,$

Name the homotopy fibers of these cocycles

as follows

$$\array{ \mathfrak{m}2\mathfrak{brane} \\ {}^{\mathllap{hofib}(\mu_{M2})}\downarrow \\ \mathbb{R}^{10,1\vert \mathbf{32}} &\underset{\mu_{M2}}{\longrightarrow}& B^3 \mathbb{R} }$$

$\,$

$\,$

$$\array{ \mathfrak{string}_{IIB} \\ {}^{\mathllap{hofib}(\mu_{F1}^B)}\downarrow \\ \mathbb{R}^{9,1\vert \mathbf{16}+ \mathbf{16}} &\underset{\mu_{F1}^B}{\longrightarrow}& B^2 \mathbb{R} } \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \array{ \mathfrak{string}_{het} \\ {}^{\mathllap{hofib}(\mu_{F1}^{het})}\downarrow \\ \mathbb{R}^{9,1\vert \mathbf{16}} &\underset{\mu_{F1}^{het}}{\longrightarrow}& B^2 \mathbb{R} } \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \array{ \mathfrak{string}_{IIA} \\ {}^{\mathllap{hofib}(\mu_{F1}^A)}\downarrow \\ \mathbb{R}^{9,1\vert \mathbf{16}+ \overline{\mathbf{16}}} &\underset{\mu_{F1}^A}{\longrightarrow}& B^2 \mathbb{R} }$$

$\,$

By prop.

the superstring super Lie 2-algebra $\mathfrak{string}_{IIA/B}$ is given by

$$CE(\mathfrak{string}_{IIA/B}) = \left\{ \array{ d e^a = \overline{\psi} \Gamma^a \psi, \; d \psi^\alpha = 0 \\ d f_2^{IIA/B} = \mu_{F1}^{IIA/B} = (\overline{\psi} \wedge \Gamma_a \psi)\wedge e^a } \right\}$$

$\,$

The membrane super Lie 3-algebra $\mathfrak{m}2\mathfrak{brane}$ is given by

$$CE(\mathfrak{m}2\mathfrak{brane}) = \left\{ \array{ d e^a = \overline{\psi} \wedge \Gamma^a \psi, \; d \psi^\alpha = 0 \\ d h_3 = \mu_{M2} = i (\overline{\psi} \wedge \Gamma_{a b} \psi) \wedge e^a \wedge e^b } \right\}$$

$\,$

This dg-algebra was first considered in D’Auria-Fré 82 (3.15)

as a tool for constructing 11-dimensional supergravity.

$\,$

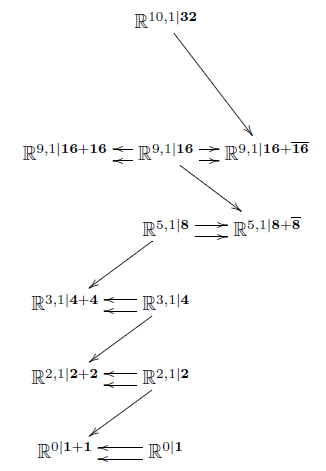
Hence the progression

of maximal invariant extensions of the superpoint

continues as a diagram

of super L-∞ algebras like so:

$\,$

$\,$

(While every extension displayed is a maximal invariant higher central extension, not all invariant higher central extensions are displayed. For instance there are string and membrane cocycles also on the lower dimensional super-Minkowski spacetimes (“non-critical”), e.g. the super 1-brane in 3d and the super 2-brane in 4d.)

$\,$

The progression of invariant higher central extensions continues:

$\,$

Proposition

(D’Auria-Fré 82, (3.27, 3.28))

The space of indecomposable invariant higher cocylces on $\mathfrak{m}2\mathfrak{brane}$ is spanned by

$$\begin{aligned} \mu_{M5} & \coloneqq \tfrac{1}{5!} \left( \overline{\psi} \wedge \Gamma_{a_1 \cdots a_5} \psi \right) \wedge e^{a_1} \wedge \cdots \wedge e^{a_5} \;+\; h_3 \wedge \mu_{M2} \\ & = \tfrac{1}{5!} \left( \overline{\psi} \wedge \Gamma_{a_1 \cdots a_5} \psi \right) \wedge e^{a_1} \wedge \cdots \wedge e^{a_5} \;+\; h_3 \, \wedge\, \tfrac{i}{2} \left( \overline{\psi} \Gamma_{a_1 a_2} \psi \right) \wedge e^{a_1} \wedge e^{a_2} \end{aligned} \,.$$

where $h_3$ is the extra generator of $CE(\mathfrak{m}2\mathfrak{brane})$.

$\,$

Proposition

(Chryssomalakos-Azcárraga-Izquierdo-Bueno 99, Sakaguchi 99)

Define the following elements in $CE(\mathfrak{string}_{IIA})$:

$$\begin{aligned} \mu_{{}_{D0}} &\coloneqq \overline{\psi}\Gamma^{10} \psi \\ \mu_{{}_{D2}} &\coloneqq (\mu_{{}_{M2}})|_{8+1} \\ & = \tfrac{i}{2} \left(\overline{\psi} \wedge \Gamma_{a_1 a_2} \psi \right) \wedge e^{a_1} \wedge e^{a_2}\;, \\ \mu_{{}_{D4}} &\coloneqq (\pi_{10})_\ast( \mu_{{}_{M5}} ) \\ & = +\tfrac{1}{4!} \left( \overline{\psi} \wedge \Gamma_{a_1\cdots a_4} \Gamma_{10}\psi \right) \wedge e^{a_1} \wedge \cdots \wedge e^{a_4} \\ \mu_{{}_{D6}} & \coloneqq \tfrac{i}{6!} \left(\overline{\psi} \Gamma_{a_1 \cdots a_6}\psi \right) \wedge e^{a_1} \wedge \cdots \wedge e^{a_6} , \\ \mu_{{}_{D8}} & \coloneqq \tfrac{1}{8!} \left( \overline{\psi} \Gamma_{a_1 \cdots a_8} \Gamma_{10} \psi \right) \wedge e^{a_1}\wedge \cdots \wedge e^{a_8} , \\ \mu_{{}_{D10}} & \coloneqq \tfrac{i}{10!} \left( \overline{\psi} \Gamma_{a_1 \cdots a_{10}} \psi \right) \wedge e^{a_1}\wedge \cdots \wedge e^{a_{10}} \,, \end{aligned}$$

Write

$$C^{IIA} \coloneqq \mu_{D0} + \mu_{D2} + \cdots + \mu_{D10}$$

for their sum.

Then the indecomposable invariant cocycles on $\mathfrak{string}_{IIA}$ are spanned by

$$\omega_{2p} \coloneqq \left[ \exp(-f_2^{IIA}) \wedge C^{IIA} \right]_{2p} \,,$$

where $f_2^{IIA}$ is the extra generator of $CE(\mathbb{R}^{9,1\vert \mathbf{16} + \overline{\mathbf{16}}})$.

Similarly define the following elements in $CE(\mathfrak{string}_{IIB})$

$$\begin{aligned} c_2^{\mathrm{IIB}} & \coloneqq \overline{\psi} \Gamma_9^{\mathrm{IIB}} \psi = \overline{\psi} \Gamma^9_B \psi\;, \\ \mu_{F1}^{\mathrm{IIB}} &:= i \left(\overline{\psi} \Gamma_a^{\mathrm{IIB}} \Gamma_{10} \psi \right) \wedge e^a \\ \mu_{{}_{D1}} & \coloneqq i \left(\overline{\psi} \Gamma_a^{\mathrm{IIB}} \Gamma_9 \psi\right) \wedge e^{a}\;, \\ \mu_{{}_{D3}} & \coloneqq \tfrac{1}{3!} \left( \overline{\psi} \Gamma^{\mathrm{IIB}}_{a_1 \cdots a_3} (\Gamma_9 \Gamma_{10}) \psi \right) \wedge e^{a_1} \wedge \cdots \wedge e^{a_3}\;, \\ \mu_{{}_{D5}} & \coloneqq \tfrac{i}{5!} \left( \overline{\psi} \Gamma^{\mathrm{IIB}}_{a_1 \cdots a_5} \Gamma_9 \psi \right) \wedge e^{a_1}\wedge \cdots \wedge e^{a_5}\;, \\ \mu_{{}_{D7}} & = \tfrac{1}{7!} \left( \overline{\psi} \Gamma^{\mathrm{IIB}}_{a_1 \cdots a_7} (\Gamma_9 \Gamma_{10}) \psi \right) \wedge e^{a_1} \wedge \cdots \wedge e^{a_7}\;, \\ \mu_{{}_{D9}} & = \tfrac{i}{9!} \left( \overline{\psi} \Gamma^{\mathrm{IIB}}_{a_1\cdots a_9}\Gamma_9 \psi \right) \wedge e^{a_1} \wedge \cdots \wedge e^{a_9}\;. \end{aligned}$$

Then the indecomposable invariant cocycles on $\mathfrak{string}_{IIB}$ are spanned by

$$\omega_{2p+2} \coloneqq \left[ \exp(-f_2^{IIB}) \wedge C^{IIB} \right]_{2p+1} \,.$$

$\,$

As above, these cocycles classify

further higher super $L_\infty$-algebra extensions

$$\array{ \mathfrak{d}p\mathfrak{brane} \\ {}^{\mathllap{hofib(\mu_{D p})}}\downarrow \\ \mathfrak{string}_{IIA/B} &\underset{\mu_{D p}}{\longrightarrow}& B^{p+1}\mathbb{R} } \;\;\;\;\;\;\;\;\,\;\;\;\;\;\;\;\;\;\;\; \array{ \mathfrak{m}5\mathfrak{brane} \\ {}^{\mathllap{hofib(\mu_{M5})}}\downarrow \\ \mathfrak{m}2\mathfrak{brane} &\underset{\mu_{M5}}{\longrightarrow}& B^6 \mathbb{R} }$$

$\,$

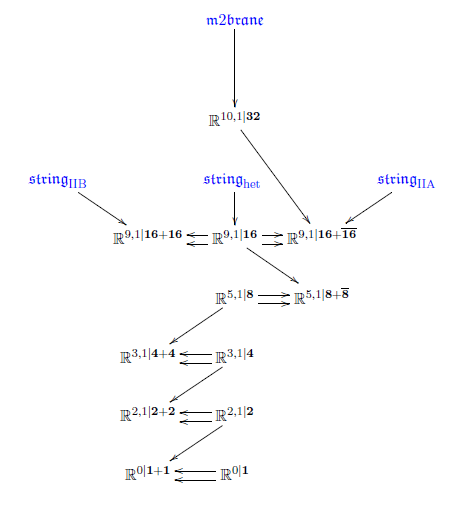
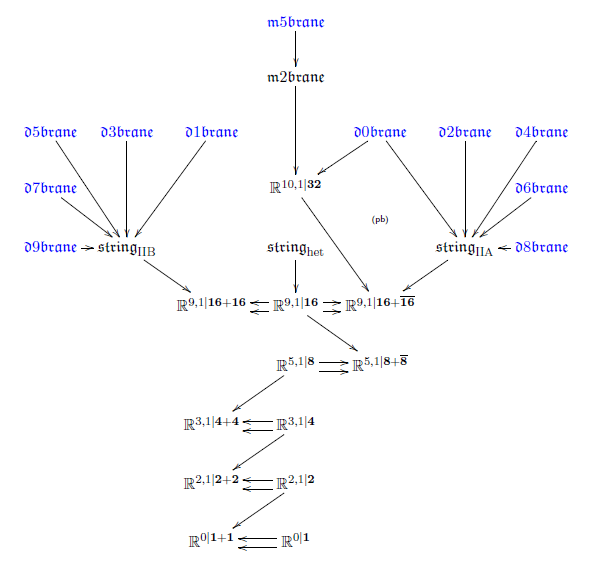
In conclusion:

by forming

iterated (maximal) invariant higher central super $L_\infty$-extensions

of the superpoint,

we obtain the following brane bouquet-diagram:

$\,$

$\,$

Fields

Now given one stage in the brane bouquet

$$\array{ \widehat{\widehat{\mathfrak{g}}} \\ {}^{\mathllap{hofib(\mu_{p_2})}}\downarrow \\ \hat \mathfrak{g} & \stackrel{\mu_{p_2}}{\longrightarrow} & B\mathfrak{h}_2 \\ {}^{\mathllap{hofib(\mu_{p_1})}}\downarrow \\ \mathfrak{g} &\overset{\mu_{p_1}}{\longrightarrow}& B\mathfrak{h}_1 }$$

we want to descend $\mu_{p_2}$ to $\mathfrak{g}$.

$\,$

By the general theory of principal ∞-bundles (Nikolaus-Schreiber-Stevenson 12):

1. $\widehat{\mathfrak{g}}$ has a $\mathfrak{h}_1$-∞-action

2. equipping $B \mathfrak{h}_2$ with an $\mathfrak{h}_1$-∞-action

   is equivalent to finding a homotopy fiber sequence as on the right here:

   $$\array{ \hat \mathfrak{g} && \stackrel{\mu_2}{\longrightarrow} && B\mathfrak{h}_2 \\ {}^{\mathllap{hofib(\mu_1)}}\downarrow && && \downarrow^{\mathrlap{hofib(p_\rho)}} \\ \mathfrak{g} && && (B\mathfrak{h}_2)/\mathfrak{h}_1 \\ & {}_{\mathllap{\mu_1}}\searrow && \swarrow_{\mathrlap{p_\rho}} \\ && B\mathfrak{h}_1 } \,.$$

3. $\mu_2$ is $\mathfrak{h}_1$-equivariant precisely if it descends to a morphism

   $$\mu_2/\mathfrak{h}_1 \;\colon\; \mathfrak{g} \longrightarrow (B\mathfrak{h}_2)/\mathfrak{h}_1$$

   such that this diagram commutes up to homotopy:

   $$\array{ \hat \mathfrak{g} && \stackrel{\mu_2}{\longrightarrow} && B\mathfrak{h}_2 \\ {}^{\mathllap{hofib(\mu_1)}}\downarrow && && \downarrow^{\mathrlap{hofib(p_\rho)}} \\ \mathfrak{g} && \stackrel{\mu_2/\mathfrak{h}_1}{\longrightarrow} && (B\mathfrak{h}_2)/\mathfrak{h}_1 \\ & {}_{\mathllap{\mu_1}}\searrow && \swarrow_{\mathrlap{p_\rho}} \\ && B\mathfrak{h}_1 } \,.$$

4. if so, then resulting triangle diagram

   $$\array{ \mathfrak{g} && \stackrel{\mu_2/\mathfrak{h}_1}{\longrightarrow} && (B\mathfrak{h}_2)/\mathfrak{h}_1 \\ & {}_{\mathllap{\mu_1}}\searrow && \swarrow_{\mathrlap{p_\rho}} \\ && B\mathfrak{h}_1 }$$

   exhibits $\mu_2/\mathfrak{h}_1$ as a cocycle in (rational) $\mu_1$-twisted cohomology

   with respect to the local coefficient bundle $p_\rho$.

$\,$

We now work out this general prescription

for the cocycles in the brane bouquet.

$\,$

RR-fields

By the brane bouquet above

the type IIA D-branes

are given by super $L_\infty$ cocycles of the form

$$\mathfrak{string}_{IIA } \overset{\mu_{Dp}}{\longrightarrow} B^{p+1}\mathbb{R}$$

for $p \in \{0,2,4,6,8,10\}$.

$\,$

Notice that

$$H^\bullet(B U, \mathbb{Z})$$

has one generator in each even degree, the universal Chern classes.

Hence the $L_\infty$-algebra

$$\mathfrak{l}(KU)$$

is given by

$$CE(\mathfrak{l}(KU)) \;\simeq\; \left\{ d \omega_{2p+2} = 0 \;\vert\; p \in \mathbb{Z} \right\} \,.$$

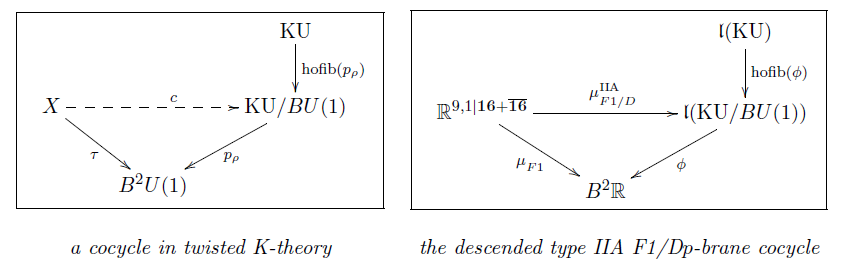
This allows to unify the D-brane cocycles

into a single morphism of super $L_\infty$-algebras of the form

$$\array{ \mathfrak{string}_{IIA} && \stackrel{\phantom{AA}\mu_D\phantom{AA}}{\longrightarrow} && \mathfrak{l}(KU) \\ {}^{\mathllap{hofib(\mu_{F1})}}\downarrow \\ \mathbb{R}^{9,1\vert \mathbf{16}+ \overline{\mathbf{16}}} \\ & {}_{\mathllap{\mu_{F1}}}\searrow \\ && B^2 \mathbb{R} } \,.$$

$\,$

By the above prescription, descending $\mu_D$ is equivalent

to finding a commuting diagram in the homotopy category of super $L_\infty$-algebras

of the form

$$\array{ \mathfrak{string}_{IIA} && \stackrel{\phantom{AA}\mu_D\phantom{AA}}{\longrightarrow} && \mathfrak{l}(KU) \\ {}^{\mathllap{hofib(\mu_{F1})}}\downarrow && && \downarrow^{\mathrlap{hofib(\phi)}} \\ \mathbb{R}^{9,1\vert \mathbf{16}+ \overline{\mathbf{16}}} &&\overset{\phantom{AA}\mu_{D}/B \mathbb{R}\phantom{AA} }{\longrightarrow}&& \text{something} \\ & {}_{\mathllap{\mu_{F1}}}\searrow && \swarrow_{\mathrlap{\phi}} \\ && B^2 \mathbb{R} } \,.$$

$\,$

This turns out to exist as follows (Fiorenza-Sati-Schreiber 16a, section 5):

Definition

Following prop. define the $L_\infty$-algebra

$$\mathfrak{l}(\,KU / BU(1)\,)$$

by

$$CE\left(\,\mathfrak{l}(\,KU / BU(1)\,)\,\right) \;=\; \left\{ \array{ d h_3 = 0\;,\; \\ d \omega_{2p+2} = h_3 \wedge \omega_{2p} } \right\} \,.$$

Moreover write

$$\mathbb{R}^{9,1\vert \mathbf{16} + \overline{\mathbf{16}}}_{res}$$

for the super $L_\infty$-algebra whose Chevalley-Eilenberg algebra is

$$CE\left( \mathbb{R}^{9,1\vert \mathbf{16} + \overline{\mathbf{16}}}_{res} \right)[f_2,h_3]/(d f_2 = \mu_{F1} + h_3)$$

$\,$

Proposition

(Fiorenza-Sati-Schreiber 16a, theorem 4.16)

The super $L_\infty$-algebra $\mathbb{R}^{9,1\vert \mathbf{16} + \overline{\mathbf{16}}}_{res}$

is a resolution of type IIA super-Minkowski spacetime.

in that there is a weak equivalence

$$\mathbb{R}^{9,1\vert \mathbf{16} + \overline{\mathbf{16}}}_{res} \stackrel{\phantom{AA}\simeq\phantom{AA}}{\longrightarrow} \mathbb{R}^{9,1\vert \mathbf{16} + \overline{\mathbf{16}}} \,.$$

This fits into a commuting diagram of the form

$$\array{ \left\{ {{d e^a = \overline{\psi}\Gamma^a \wedge \psi } \atop {d \psi^\alpha = 0}} \atop { d f_2 = \mu_{F1}} \right\} && \mathfrak{string}_{IIA} && \stackrel{ \mu_D }{\longrightarrow} && \mathfrak{l}(KU) && \left\{ d \omega_{2 p+2} = 0 \right\} \\ && \downarrow^{\mathrlap{hofib(\mu_{F1})}} && && \downarrow^{\mathrlap{\phi}} \\ \left\{ {{d e^a = \overline{\psi}\Gamma^a \wedge \psi } \atop {d \psi^\alpha = 0}} \atop { d f_2 = \mu_{F1} + h_3 } \right\} & & \mathbb{R}_{res}^{9,1\vert \mathbf{16}+ \overline{\mathbf{16}}} && \stackrel{ \mu_{F1/D} }{\longrightarrow} && \mathfrak{l}(KU / B U(1)) && \left\{ \array{ h_3 = 0 \\ d\omega_{2p+2} = h_3\wedge \omega_{2p} } \right\} \\ && & {}_{\mathllap{\mu_{F 1}}}\searrow && \swarrow_{\mathrlap{\phi}} \\ && && B^2 \mathbb{R} \\ && && \left\{ d h_3 = 0 \right\} } \,.$$

$\,$

In conclusion

$\;\;$the type IIA F1-brane and D-brane cocycles with $\mathbb{R}$-coefficients

$\;\;$do descend to super-Minkowski spacetime

$\;\;$as one single cocycle with coefficients

$\;\;$in rationalized twisted K-theory.

$\,$

M-flux fields

(skip)

The part of the brane bouquet giving the M-branes is

$$\array{ \mathfrak{m}2\mathfrak{brane} &\stackrel{\mu_{M5}}{\longrightarrow}& B^6 \mathbb{R} \\ {}^{\mathllap{hofib(\mu_{M2})}}\downarrow \\ \mathbb{R}^{10,1\vert \mathbf{32}} & \stackrel{\mu_{M2}}{\longrightarrow} & B^3 \mathbb{R} \\ {}^{\mathllap{hofib(\mu_{D 0})}}\downarrow \\ \mathbb{R}^{9,1\vert \mathbf{16} + \overline{\mathbf{16}}} }$$

$\,$

In order to descend this, consider the $L_\infty$-algebra corresponding to the 4-sphere

$$\mathfrak{l}(\,S^4\,) \,.$$

By standard facts on rational n-spheres, this is given by

$$CE(\mathfrak{l}S^4) \;\simeq\; \left\{ \array{ d \, g_4 = 0\,,\, \\ d\, g_7 + \tfrac{1}{2} g_4 \wedge _4 = 0 } \right\} \,.$$

Proposition

(Fiorenza-Sati-Schreiber 15, section 3)

There is a homotopy fiber sequence of $L_\infty$-algebras as on the right

$$\left( \array{ && S^7 \\ && \downarrow \\ && S^4 \\ & \swarrow \\ B SU(2) \\ \downarrow^{\mathrlap{c_2}} \\ B^3 U(1) } \right) \;\; \stackrel{\phantom{AA}\mathfrak{l}(-)\phantom{AA} }{\mapsto} \;\; \left( \array{ && B^6 \mathbb{R} \\ && \downarrow^{\mathrlap{ hofib(\mathfrak{l}(c_2)) } } \\ &&\mathfrak{l}(S^4) \\ & \swarrow_{\mathfrak{l}(c_2)} \\ B^3 \mathbb{R} } \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \right)$$

which is the image under $\mathfrak{l}(-)$ of the quaternionic Hopf fibration.

This makes a commuting diagram

in the homotopy category of super $L_\infty$-algebas

of the form

$$\array{ \left\{ { { d e^a = \overline{\psi}\wedge \Gamma^a \wedge \psi } \atop { d \psi^\alpha = 0 } } \atop d h_3 = - \mu_{M2} \right\} && \mathfrak{m}2\mathfrak{brane} && \stackrel{ \mu_{M5} }{\longrightarrow} && B^6 \mathbb{R} && \left\{ d g_7 = 0 \right\} \\ && \downarrow^{\mathrlap{hofib(\mu_{M2})}} && && \downarrow^{\mathrlap{hofib(\mathfrak{l}(c_2))}} \\ \left\{ { { d e^a = \overline{\psi}\wedge \Gamma^a \wedge \psi } \atop { d \psi^\alpha = 0 } } \atop d h_3 = g_4 - \mu_{M2} \right\} && \mathbb{R}_{res}^{10,1\vert\mathbf{32}} && \stackrel{ \mu_{M2/M5} }{\longrightarrow} && \mathfrak{l} S^4 && \left\{ {d g_4 = 0} \atop {d g_7 + \tfrac{1}{2} g_4 \wedge g_4 = 0} \right\} \\ && & {}_{\mathllap{\mu_{M2}}}\searrow && \swarrow_{\mathrlap{\mathfrak{l}(c_2)}} \\ && && B^3 \mathbb{R} \\ && && \left\{ d g_4 = 0\right\} }$$

In conclusion

$\;\;$this says that, rationally,

$\;\;$M2-brane charge is in degree-4 ordinary cohomology

$\;\;$and it twists M5-brane charge

$\;\;$which is, rationally, in unstable degree-4 cohomotopy.

$\,$

Now that we have found

the descended $L_\infty$-cocycles

for all super $p$-branes

in twisted cohomology, rationally,

we may analyze their behaviour under double dimensional reduction

and discover the super $L_\infty$-algebraic incarnation

of various dualities in string theory.

$\,$

$\,$

Reduction

$\,$

We have discovered higher cocycles

on higher dimensional super-spacetimes.

Now we discuss that there is double dimensional reduction

which takes these to lower-degree cocycle on lower-dimensional space.

This is given by passage to cyclic loop spaces:

$\,$

Proposition

Let $\mathbf{H}$ be any (∞,1)-topos

such as

• the classical homotopy theory on topological spaces

• the homotopy theory of supergeometric homotopy types discussed below

and let $G \in Grp(\mathbf{H})$ be an ∞-group in $\mathbf{H}$,

then right base change along $\ast \to \mathbf{B}G$ is a pair of adjoint ∞-functors of the form

$$\mathbf{H} \underoverset {\underset{\phantom{AA}[G,-]/G \phantom{AA}}{\longrightarrow}} {\overset{\phantom{AA} hofib \phantom{AA} }{\longleftarrow}} {\bot} \mathbf{H}_{/\mathbf{B}G} \,,$$

where

• $[G,-]$ denotes the internal hom in $\mathbf{H}$,

• $[G,-]/G$ denotes the homotopy quotient by the conjugation

∞-action for $G$ equipped with its canonical ∞-action by left multiplication and the argument

regarded as equipped with its trivial $G$-$\infty$-action;

for $G = S^1$ the circle group, then this is the cyclic loop space $\mathcal{L}(-)/S^1$.

Hence for

• $\hat X \to X$ a $G$-principal ∞-bundle

• $A \in \mathbf{H}$ any coefficient object,

  such as for some differential generalized cohomology theory, discussed below

then there is a natural equivalence

$$\underset{ \text{original} \atop \text{fluxes} }{ \underbrace{ \mathbf{H}(\hat X\;,\; A) } } \;\; \underoverset {\underset{oxidation}{\longleftarrow}} {\overset{reduction}{\longrightarrow}} {\simeq} \;\; \underset{ \text{doubly} \atop { \text{dimensionally reduced} \atop \text{fluxes} } }{ \underbrace{ \mathbf{H}(X \;,\; [G,A]/G) } }$$

given by

$$\left\{ \array{ \hat X &\overset{\phi}{\longrightarrow}& A \\ \downarrow^{{\mathrlap{hofib(c)}}} \\ X \\ & {}_{\mathllap{c}}\searrow \\ && \mathbf{B} G } \right\} \;\;\; \leftrightarrow \;\;\; \left\{ \array{ X && \overset{\tilde \phi}{\longrightarrow} && [G,A]/G \\ & {}_{\mathllap{c}}\searrow && \swarrow \\ && \mathbf{B}G } \right\}$$

Proof

(skip proof)

First observe that the conjugation action on $[G,X]$ is the internal hom in the (∞,1)-category of $G$-∞-actions $Act_G(\mathbf{H})$. Under the equivalence of (∞,1)-categories

$$Act_G(\mathbf{H}) \simeq \mathbf{H}_{/\mathbf{B}G}$$

(from Nikolaus-Schreiber-Stevenson 12) then $G$ with its canonical ∞-action is $(\ast \to \mathbf{B}G)$ and $X$ with the trivial action is $(X \times \mathbf{B}G \to \mathbf{B}G)$.

Hence

$$[G,X]/G \simeq [\ast, X \times \mathbf{B}G]_{\mathbf{B}G} \;\;\;\;\; \in \mathbf{H}_{/\mathbf{B}G} \,.$$

Actually, this is the very definition of what $[G,X]/G \in \mathbf{H}_{/\mathbf{B}G}$ is to mean in the first place, abstractly.

But now since the slice (∞,1)-topos $\mathbf{H}_{/\mathbf{B}G}$ is itself cartesian closed, via

$$E \times_{\mathbf{B}G}(-) \;\;\; \dashv \;\;\; [E,-]_{\mathbf{B}G}$$

it is immediate that there is the following sequence of natural equivalences

$$\begin{aligned} \mathbf{H}_{/\mathbf{B}G}(Y, [G,X]/G) & \simeq \mathbf{H}_{/\mathbf{B}G}(Y, [\ast, X \times \mathbf{B}G]_{\mathbf{B}G}) \\ & \simeq \mathbf{H}_{/\mathbf{B}G}( Y \times_{\mathbf{B}G} \ast, \underset{p^\ast X}{\underbrace{X \times \mathbf{B}G }} ) \\ & \simeq \mathbf{H}( \underset{hofib(Y)}{\underbrace{p_!(Y \times_{\mathbf{B}G} \ast)}}, X ) \\ & \simeq \mathbf{H}(hofib(Y),X) \end{aligned}$$

Here $p \colon \mathbf{B}G \to \ast$ denotes the terminal morphism and $p_! \dashv p^\ast$ denotes the base change along it.

$\,$

We now apply this general mechanism to the brane bouquet.

$\,$

By the discussion of rational homotopy theory above

we may think of L-∞ algebras as rational topological spaces

and more generally as rational parameterized spectra.

For instance above we found that the coefficient space

for RR-fields in rational twisted K-theory is the

L-∞ algebra$\mathfrak{l}(KU/BU(1))$.

$\,$

Hence in order to apply double dimensional reduction

to super p-branes

we now specialize the above formalization to

cyclification of super L-∞ algebras (FSS 16b)

$\,$

Definition

For $\mathfrak{g}$ any super L-∞ algebra of finite type, its cyclification

$$\mathfrak{L}\mathfrak{g}/\mathbb{R} \in s L_\infty Alg_{\mathbb{R}}$$

is defined by having Chevalley-Eilenberg algebra of the form

$$CE(\mathfrak{L}\mathfrak{g}/\mathbb{R}) \coloneqq \left( \wedge^\bullet \left( \underset{\text{original}}{\underbrace{\mathfrak{g}^\ast}} \oplus \underset{\text{shifted copy}}{\underbrace{s\mathfrak{g}^\ast}} \oplus \underset{\text{new generator} \atop \text{in degree 2}}{\underbrace{\langle \omega_2 \rangle}} \right) \;,\; d_{\mathfrak{d}\mathfrak{g}/\mathbb{R}} \;\colon\; \left\{ \array{ \omega_2 &\mapsto& 0 \\ \alpha &\mapsto& d_{\mathfrak{g}} \alpha + \omega_2 \wedge s \alpha \\ s \alpha &\mapsto& - s d_{\mathfrak{g}} \alpha } \right. \right)$$

where

$$s \mathfrak{g}^\ast$$

is a copy of $\mathfrak{g}^\ast$ with cohomological degrees shifted down by one, and where $\omega$ is a new generator in degree 2.

The differential is given for $\alpha \in \wedge^1 \mathfrak{g}^\ast$ by

$$d_{\mathfrak{d}\mathfrak{g}/\mathbb{R}} \;\colon\; \left\{ \array{ \omega_2 &\mapsto& 0 \\ \alpha &\mapsto& d_{\mathfrak{g}} \alpha \pm \omega_2 \wedge s \alpha \\ s \alpha &\mapsto& - s d_{\mathfrak{g}} \alpha } \right.$$

where on the right we are extendng $s$ as a graded derivation.

Define

$$\mathfrak{L}\mathfrak{g} \in s L_\infty Alg_{\mathbb{R}}$$

in the same way, but with $\omega_2 \coloneqq 0$.

For every $\mathfrak{g}$ there is a homotopy fiber sequence

$$\array{ && \mathfrak{L}\mathfrak{g} \\ && \downarrow \\ && \mathfrak{L} \mathfrak{g}/\mathbb{R} \\ & \swarrow_{\mathrlap{\omega_2}} \\ B \mathbb{R} }$$

which hence exhibits $\mathfrak{L} \mathfrak{g}/\mathbb{R}$ as the homotopy quotient of $\mathfrak{L}\mathfrak{g}$ by an $\mathbb{R}$-action.

$\,$

The following says that the $L_\infty$-cyclification from prop.

indeed does model correspond to the topological cyclification .

$\,$

Proposition

(Vigué-Sullivan 76, Vigué-Burghelea 85)

If

$$\mathfrak{g} = \mathfrak{l}(\,X\,)$$

is the $L_\infty$-algebra associated by rational homotopy theory to a simply connected topological space $X$,

then its cyclification (def. )

corresponds to the cyclic loop space of $X$

$$\mathfrak{L}( \;\mathfrak{l}( X )\; )/\mathbb{R} \simeq \mathfrak{l}( \;\mathcal{L}X/S^1\; ) \,.$$

The cochain cohomology of the Chevalley-Eilenberg algebra

$$CE(\mathfrak{l}( \;\mathcal{L}X/S^1\; ))$$

computes the cyclic cohomology of $X$ with coefficients in $\mathbb{R}$.

Moreover the homotopy fiber sequence of the cyclification corresponds to that of the free loop space:

$$\left( \array{ \mathcal{L}X \\ \downarrow^{\mathrlap{hofib(p)}} \\ \mathcal{L}X/S^1 \\ \downarrow^{\mathrlap{p}} \\ B S^1 } \;\;\;\;\;\;\;\; \right) \;\;\;\; \stackrel{\phantom{AA}\mathfrak{l}(-)\phantom{AA}}{\mapsto} \;\;\;\; \left( \array{ \mathfrak{L} \mathfrak{l}(X) \\ \downarrow^{ \mathrlap{ hofib( \mathfrak{l}(p) ) } } \\ \mathfrak{L}\mathfrak{l}(X)/\mathbb{R} \\ \downarrow^{\mathrlap{\mathfrak{l}(p)}} \\ B \mathbb{R} } \;\;\;\;\;\;\;\; \right)$$

$\,$

We now have the following super $L_\infty$-algebraic incarnation

of the general double dimensional reduction from prop. :

$\,$

Proposition

(Fiorenza-Sati-Schreiber 16b, prop. 3.5)

Let

$$\array{ \widehat{\mathfrak{g}} \\ {}^{\mathllap{\pi}}\downarrow \\ \mathfrak{g} \\ & {}_{\mathllap{\mu_2}}\searrow \\ && B \mathbb{R} }$$

be a central extension of super L-∞ algebras. According to prop. we have

$$CE(\widehat{\mathfrak{g}}) \simeq CE(\mathfrak{g})[e]/(d e = \mu_2) \,.$$

and hence every generator $\alpha_p \in CE(\widehat{\mathfrak{g}})$ has a unique decomposition

$$\alpha_p = \beta_p - e \wedge \tilde \alpha_{p-1}$$

where $\beta_p$ and $\tilde \alpha_{p-1}$ do not involve the generator $e$. We may think of this as

$$\pi_\ast(\alpha_p) \coloneqq \tilde \alpha_{p-1} \;\;\;\;\,\; \alpha_p|_{\mathfrak{g}} \coloneqq \beta_p \,.$$

Under this identification any super $L_\infty$-homomorphism

$$\phi \;\colon\; \widehat{\mathfrak{g}} \overset{\phi}{\longrightarrow} \mathfrak{h}$$

hence a dg-algebra homomorphism

$$\phi^\ast \;\colon\; CE(\mathfrak{h}) \longrightarrow CE(\widehat{\mathfrak{g}})$$

gives rise to a homomorphism of the form

$$\tilde \phi \;\colon\; \mathfrak{g} \longrightarrow \mathfrak{L}\mathfrak{g}/\mathbb{R}$$

which, in the notation of def. , is given dually by

$$\tilde \phi^\ast \colon \left\{ \array{ \alpha & \mapsto (\phi^\ast \alpha)|_{\mathfrak{g}} \\ s \alpha & \mapsto \pi_\ast(\phi^\ast \alpha) \\ \omega_2 & \mapsto \mu_2 } \right. \,.$$

Moreover, this construction constitutes a natural bijection

$$\array{ \underset{ \text{original} \atop \text{cocycles} }{ \underbrace{ Hom( \widehat{\mathfrak{g}}, \mathfrak{h} ) }} \;&\; \underoverset {\underset{oxidation}{\longleftarrow}} {\overset{reduction}{\longrightarrow}} {\simeq} \;&\; \underset{ \text{doubly} \atop { \text{dimensionally reduced} \atop \text{cocycles} } }{ \underbrace{ Hom_{/B\mathbb{R}}( \mathfrak{g}, \mathfrak{L}\mathfrak{h}/\mathbb{R} ) } } \\ \\ \text{given by} \\ \\ \left\{ \array{ \widehat{\mathfrak{g}} &\overset{\mu}{\longrightarrow}& \mathfrak{h} \\ \downarrow^{\mathrlap{hofib(c_2)}} \\ \mathfrak{g} \\ & {}_{\mathllap{c_2}}\searrow \\ && B \mathbb{R} } \right\} \;&\; \leftrightarrow \;&\; \left\{ \array{ \mathfrak{g} && \overset{\tilde \mu}{\longrightarrow} && \mathfrak{L}\mathfrak{h}/\mathbb{R} \\ & {}_{\mathllap{\mu_2}}\searrow && \swarrow_{\mathrlap{\omega_2}} \\ && B \mathbb{R} } \right\} }$$

between super $L_\infty$-homomorphisms out of the exteded super $L_\infty$-algebra $\widehat{\mathfrak{g}}$ and homomorphism out of the base $\mathfrak{g}$ into the cyclification (def. ) of the original coefficients with the latter constrained so that the canonical 2-cocycle on the cyclification is taken to the 2-cocycle classifying the given extension.

$\,$

Example

(skip example)

Let

$$\left[ \array{ \widehat{\mathfrak{g}} \\ \downarrow \\ \mathfrak{g} \\ & {}_{}\searrow \\ && b \mathbb{R} } \right] \;\coloneqq\; \left[ \array{ \mathbb{R}^{d,1\vert N_{d+1}} \\ \downarrow \\ \mathbb{R}^{d-1,1\vert N_d} \\ & {}_{\mathllap{\overline{\psi}\wedge \Gamma^{d}\psi}} \searrow \\ && b \mathbb{R} } \right]$$

be the extension of a super Minkowski spacetime from dimension $d$ to dimension $d+1$.

Let moreover

$$\mathfrak{h} \coloneqq b^{(p+1)+1} \mathbb{R}$$

be the line Lie (p+3)-algebra

and consider any super (p+1)-brane cocycle from the old brane scan in dimension $d+1$

$$\mu_{(p+1)+2} \;\coloneqq\; \underoverset{a_i = 0}{d}{\sum} \left( \overline{\psi} \wedge \Gamma_{a_1 \cdots a_{p+1}} \psi \right) \wedge e^{a_1} \wedge \cdots \wedge e^{a_{p+1}} \;\;\colon\;\; \mathbb{R}^{d,1\vert N_{d+1}} \longrightarrow b^{p+1} \mathbb{R} \,.$$

Then the cyclification $\mathfrak{L}(b^{p+1}\mathbb{R})/\mathbb{R}$ of the coefficients (prop. ) is

$$CE\left( \, \mathfrak{L}(b^{p+2}\mathbb{R})/\mathbb{R} \, \right) \;=\; \left\{ \array{ d \omega_2 = 0 \\ d \omega_{p + 2} = 0 \\ d \omega_{(p+1)+2} = \omega_{p+1} \wedge \omega_2 } \right\}$$

and the dimensionally reduced cocycle

$$\array{ \mathbb{R}^{d-1,1\vert N_d} && \overset{}{\longrightarrow} && \mathfrak{L}(b^{p+1}\mathbb{R})/\mathbb{R} \\ & \searrow && \swarrow \\ && b \mathbb{R} }$$

has the following components

$$\array{ && && \overset{ p+1\text{-brane} }{ \overbrace{ { \mu^{d+1}_{(p+1)+2} = } \atop { \underoverset{d=0}{d}{\sum} \left( \overline{\psi} \wedge \Gamma_{a_1 \cdots a_{p+1}} \psi \right) \wedge e^{a_1} \wedge \cdots e {a_{p+1}} } } } \\ && & {}^{\mathllap{\text{wrapped}}}\swarrow && \searrow^{\mathrlap{\text{not} \atop \text{wrapped}}} \\ \underset{ \text{0-brane} }{ \underbrace{ { \mu^{d}_{0+2} = } \atop { \left( \overline{\psi} \wedge \Gamma^d \psi \right) } } } && \underset{ p\text{-brane} }{ \underbrace{ { \mu^{d}_{p+2} = } \atop { \underoverset{a_i = 0}{d-1}{\sum} \left( \overline{\psi} \wedge \Gamma_{a_1 \cdots a_{p}} \psi \right) \wedge e^{a_1} \wedge \cdots e^{a_p} } } } && && \underset{ p+1\text{-brane} }{ \underbrace{ { \mu^{d}_{p+2} = } \atop { \underoverset{a_i = 0}{d-1}{\sum} \left( \overline{\psi} \wedge \Gamma_{a_1 \cdots a_{p+1}} \psi \right) \wedge e^{a_1} \wedge \cdots e^{a_{p+1}} } } } }$$

It follows that with

$$d \,\mu^{d+1}_{(p+1)+2} = 0$$

also

$$d\, \mu^d_{p+2} = 0 \,.$$

This is the dimensional reduction observed in the old brane scan (Achúcarro-Evans-Townsend-Wiltshire 87)

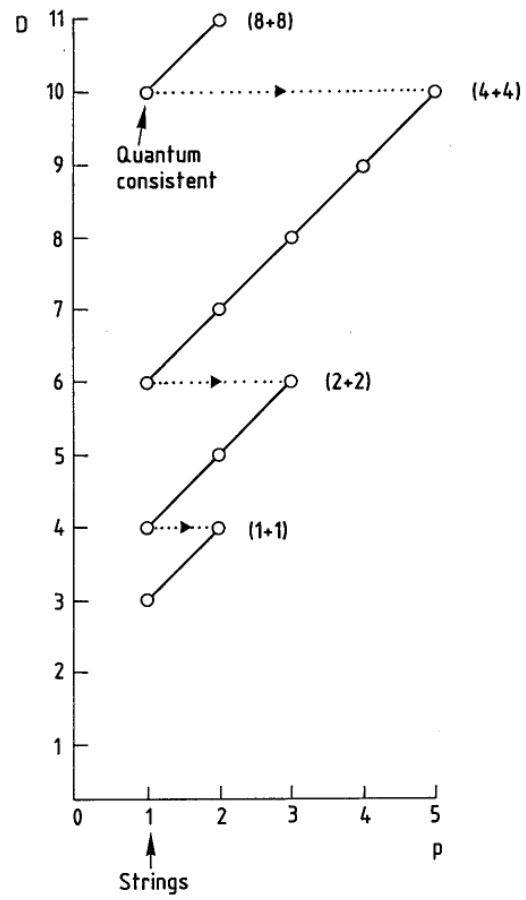
graphics grabbed from (Duff 87)

But there is more: the un-wrapped component of the dimensionally reduced cocycle satisfies the twisted cocycle condition

$$d \, \mu^d_{(p+1)+2} \;=\; \mu^d_{p+2} \wedge \mu^d_{0+2} \,.$$

These relations are not to be ignored.

This we turn to now.

$\,$

$\,$

T-Duality

$\,$

We consider now the D-brane cocycles

on type IIA and IIB superspacetime

and dimensionally reduce both to their joint 9d base space.

There we discover a hidden duality: T-duality.

$\,$

Proposition

(Fiorenza-Sati-Schreiber 16b, prop. 5.1)

The cyclification $\mathfrak{L}\mathfrak{l}(\mathrm{KU}/BU(1))/\mathbb{R}$ (def. ) of $\mathfrak{l}(\mathrm{KU}/BU(1))$ (def. ) has CE-algebra

$$\mathrm{CE}(\mathfrak{L}\mathfrak{l}(\mathrm{KU}/BU(1))/\mathbb{R}) = \left\{ \array{ d c_2 = 0\,,\;\;\;\;d \tilde c_2 = 0 \\ d h_3 = - c_2 \wedge \tilde c_2 \\ d \omega_{2p+2} = h_3 \wedge \omega_{2p} + c_2 \wedge \omega_{2p+1} \\ d \omega_{2p+1} = h_3 \wedge \omega_{2p-1} + \tilde c_2 \wedge \omega_{2p} } \right\}\;.$$

The cyclification $\mathfrak{L}\mathfrak{l}(\Sigma\mathrm{KU}/BU(1))/\mathbb{R}$ of $\mathfrak{l}(\Sigma\mathrm{KU}/BU(1))$ has CE-algebra

$$\mathrm{CE}(\mathfrak{L}\mathfrak{l}(\Sigma\mathrm{KU}/BU(1))/\mathbb{R}) = \left\{ \begin{array}{l} d c_2 = 0 \,, \;\;\;\; d \tilde c_2 = 0 \\ d h_3 = - c_2 \wedge \tilde c_2 \\ d \omega_{2p+2} = h_3 \wedge \omega_{2p} + \tilde c_2 \wedge \omega_{2p+1} \\ d \omega_{2p+1} = h_3 \wedge \omega_{2p-1} + c_2 \wedge \omega_{2p} \end{array} \right\}\;.$$

Hence there is an $L_\infty$-isomorphism of the form

$$\phi_T \;:\; \mathfrak{l}( \mathcal{L}(\mathrm{KU}/BU(1))/S^1 ) \underoverset{\simeq}{\phantom{AA}\phi_T \phantom{AA}}{\longrightarrow} \mathfrak{l}( \mathcal{L}(\Sigma\mathrm{KU}/BU(1))/S^1 )$$

relating the cyclifications of the rational twisted KU-coefficients, which is given by

$$c_2 \leftrightarrow \tilde c_2\;, \qquad h_3 \mapsto h_3\;, \qquad \omega_{p} \mapsto \omega_p \;.$$

Proof

(skip proof)

By def. , as a polynomial algebra the CE-algebra of $\mathfrak{L}\mathfrak{l}(\mathrm{KU}/BU(1))$ is obtained from the CE-algebra of $\mathfrak{l}(\mathrm{KU}/BU(1))$ by adding a shifted copy of each generator. We denote by $\omega_{2p-1}$ the shifted copy of $\omega_{2p}$ and by $-\tilde{c}_2$ the shifted copy of $h_3$. The differential is then defined by

$$d\omega_{2p+2}=h_3 \wedge \omega_{2p}\;, \qquad d\omega_{2p+1}=h_3 \wedge \omega_{2p-1} + \tilde{c}_2\wedge \omega_{2p}\;, \qquad dh_3=0,\qquad d\tilde{c}_2=0\;.$$

Next, again by def. , the CE-algebra of $\mathfrak{L}\mathfrak{l}(\mathrm{KU}/BU(1))/\mathbb{R}$ is obtained by adding a further degree 2 generator $c_2$ and defining the differential as

$$\array{ d\omega_{2p+2}= h_3 \wedge \omega_{2p} + c_2\wedge \omega_{2p+1}\;, & \qquad d\omega_{2p+1}= h_3 \wedge \omega_{2p-1} + \tilde{c}_2\wedge \omega_{2p}\;, \\ dc_2=0\;, \qquad d\tilde{c}_2=0\;, & \qquad \quad dh_3= - c_2\wedge \tilde{c}_2\;. }$$

The proof for $\mathfrak{L}\mathfrak{l}(\Sigma\mathrm{KU}/BU(1))/\mathbb{R}$ is completely analogous.

$\,$

Hence postcomposition with $\phi_T$

sends the doubly dimensionally reduced IIA/B D-brane cocycles

to some other super $L_\infty$-cocycles.

The following theorem says that

indeed it takes them into each other:

$\,$

Theorem

(Fiorenza-Sati-Schreiber 16b, theorem 5.3)

The following diagram commutes

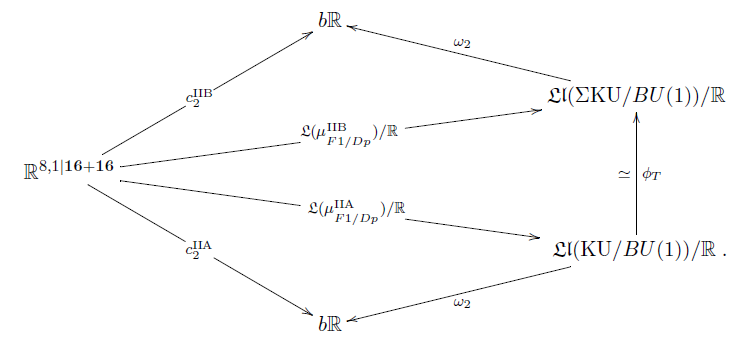
In particular this means that

1. $(\pi^{IIA/IIB}_9)_\ast \left( \mu^{IIA/IIB}_{F1} \right) = - c_2^{IIB/IIA}$.

2. $(\pi_9^{IIA})_\ast - e_9^{IIA} \wedge (-)\vert_{8+1} \;\colon\; C^{IIA} \mapsto C^{IIB}$.

$\,$

The first of these two conditions is

the super $L_\infty$-version of the axiom for

topological T-duality due to Bouwknegt-Evslin-Mathai 04.

$\,$

$\,$

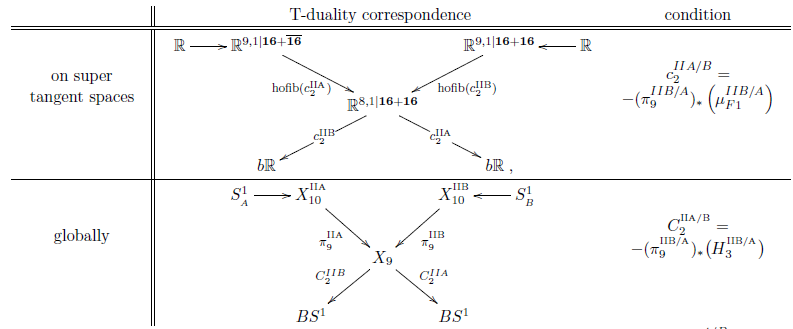
To understand the second condition

pass to the correspondence super $L_\infty$-algebra.

$\,$

Proposition

(Fiorenza-Sati-Schreiber 16b, prop. 6.2)

We have a diagram of super $L_\infty$-algebras of the following form

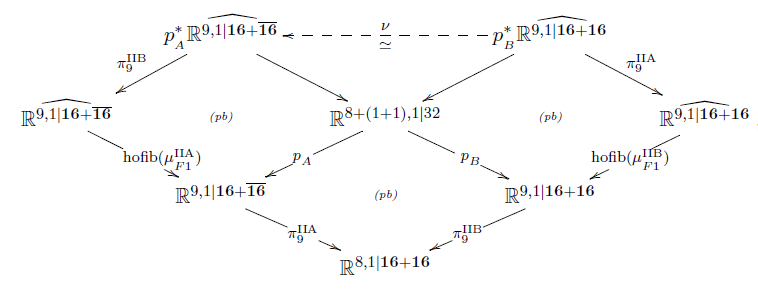
such that on the classifying 3-cocycles

$\nu$ is given by the Poincaré form

$$\mathcal{P} := e_9^{\mathrm{IIA}} \wedge e_9^{\mathrm{IIB}}$$

as

$$p_B^\ast (\mu_{{}_{F1}}^{\mathrm{IIB}} )- p_A^\ast (\mu_{{}_{F1}}^{\mathrm{IIA}}) = d \mathcal{P} \,.$$

$\,$

This now is the super $L_\infty$-version of the

refined formulation of topological T-duality

due to Bunke-Schick 04:

$\,$

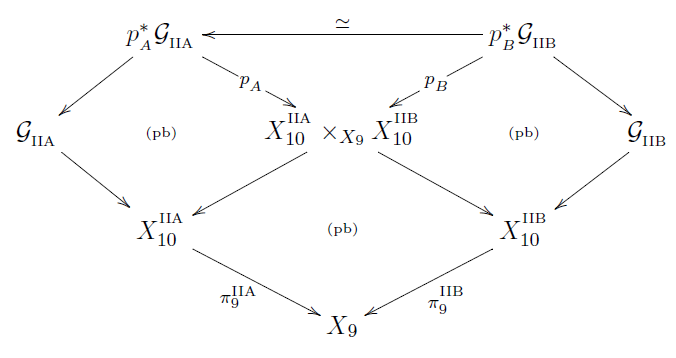
Proposition

(Fiorenza-Sati-Schreiber 16b, prop. 6.4)

The integral transform of pull-push through this correspondence is an isomorphism

$$(\pi_9^{\mathrm{IIA}})_\ast \circ \nu^\ast \circ (\pi_9^{\mathrm{IIB}})^\ast \;:\; H_{\mu_{F1}^{\mathrm{IIA}}} \left( \mathbb{R}^{9,1\vert \mathbf{16} + \overline{\mathbf{16}}}, \mathfrak{l}(\mathrm{KU}) \right) \longrightarrow H_{\mu_{F1}^{\mathrm{IIB}}} \left( \mathbb{R}^{9,1\vert \mathbf{16} + {\mathbf{16}}}, \mathfrak{l}(\Sigma \mathrm{KU}) \right)$$

Moreover, it identifies the type IIA D-brane cocycles with those of type IIB (from def. ), as in Theorem :

$$\begin{aligned} \exp(-f_2^{\mathrm{IIB}}) \wedge C^{\mathrm{IIB}} & =\; (\pi_9^{\mathrm{IIA}})_\ast \circ \nu^\ast \circ (\pi_9^{\mathrm{IIB}})^\ast \left( \exp(-f_2^{\mathrm{IIA}}) \wedge C^{\mathrm{IIA}} \right) \\ & =\; (\pi_9^{\mathrm{IIA}})_\ast \left(\, \exp(\mathcal{P}) \wedge (\pi_9^{\mathrm{IIB}})^\ast \left( \, \exp(-f^{\mathrm{IIA}}_2) \wedge C^{\mathrm{IIA}} \, \right) \,\right) \end{aligned} \,,$$

Proof

One checks that

$$(\pi_9^{\mathrm{IIA}})_\ast \left( \exp(\mathcal{P}) \wedge (\pi_9^{\mathrm{IIB}})^\ast \left( - \right) \right) = (\pi_9^{\mathrm{IIA}})_\ast(-) - e_9^{IIA} \wedge (- )\vert_{8+1} \,.$$

With this the statement follows from theorem , item 2.

$\,$

$\,$

Prop. is the super $L_\infty$-algebraic analog of Bunke-Schick 04, theorem 3.13.

In fact on CE-algebras this is the Buscher rules for RR-fields

also known as Hori’s formula (Hori 99).

$\,$

To see why the above correspondence

follows from the double dimensional reduction isomorphism $\phi_T$

it is useful to break up the doubly dimensionally reduced cocycles $\mathcal{L}( \, \mu_{F1,Dp}^{IIA/B} \, )$

into the part for the fiber bundle and the part for the K-cocycles:

$\,$

Definition

The delooped T-duality Lie 2-algebra $B \mathcal{T}_1$

is the homotopy fiber of the cup square of the first Chern class

$$B \mathcal{T}_1 \overset{}{\longrightarrow} B \mathbb{R} \oplus B \mathbb{R} \overset{\phantom{A}c_1 \cup \tilde c_1 \phantom{A}}{\longrightarrow} B^3 \mathbb{R}$$

hence by prop.

$$CE( B \mathcal{T}_1 ) \;=\; \left\{ \array{ d c_2 = 0, \;\; d \tilde c_2 = 0 \\ d h_3 = - c_2 \wedge \tilde c_2 } \right\} \,.$$

$\,$

Proposition

(FSS 16b, prop. 7.3)

The dimensionally reduced twisted K-theory coefficients from prop.

sit in a homotopy fiber sequence of the form

$$\array{ \mathfrak{l}(\, KU \oplus \Sigma KU \,) &\longrightarrow& \mathfrak{l}(\, \mathcal{L}( KU/BU(1))/S^1 \,) \\ && \downarrow \\ && B \mathcal{T}_1 }$$

exhibiting (via NSS 12) an ∞-action

of the T-duality Lie 2-algebra from def.

on $\mathfrak{l}(\, KU \oplus \Sigma KU \,)$.

$\,$

Proposition

(FSS 16b, prop. 7.5)

The homotopy fiber of the cyclified IIA/B cocycles (theorem )

projected to the T-duality Lie 2-algebra $B \mathcal{T}_1$ (def. )

are the super $L_\infty$-algeberas $p_{A}^\ast \widehat{ \mathbb{R}^{9,1 \vert \mathbf{16} + \overline{\mathbf{16}}} }$ and $p_B^\ast( \widehat{ \mathbb{R}^{9,1\vert \mathbf{16} + \mathbf{16}} } )$ from prop.

hence the Bunke-Schick 04-type correspondence

follows from theorem

via $\infty$-functoriality of homotopy fibers:

$\,$

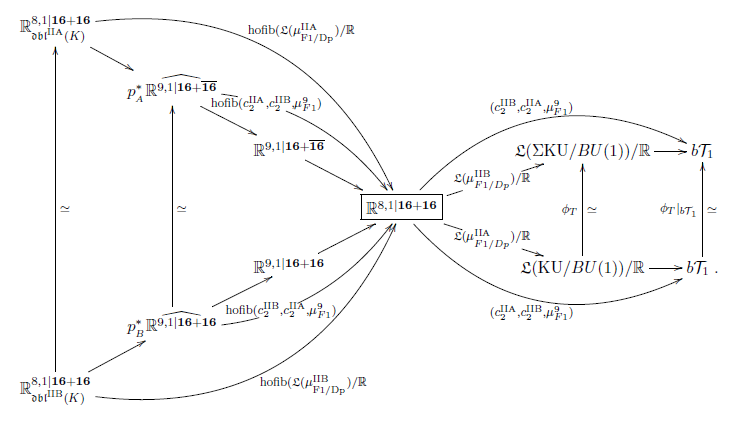
Prop. implies that we may study T-duality

in terms of principal 2-bundles for the T-duality 2-group

over 9d super-manifolds locally modeled on $\mathbb{R}^{8,1\vert \mathbf{16} + \mathbf{16}}$.

This is the supergeometric refinement

of the 2-bundle perspective on T-folds due to (Nikolaus 14).

$\,$

$\,$

Integral lift

The above super $L_\infty$-algebra

is to be the curvature/Chern character data

of twisted differential cohomology

on supermanifolds.

$\,$

Consider the (∞,1)-topos over the site of all super-formal manifolds

$$\mathbf{H} \coloneqq Sh_\infty( SuperFormalMfd ) \,.$$

Hence $X \in \mathbf{H}$ is a “super formal smooth ∞-groupoid”.

$\,$

Proposition

(Schreiber, dcct)

This (∞,1)-topos $\mathbf{H}$ carries a progression of adjoint modalities

as shown on the right

where

1. each item denotes an idempotent (∞,1)-(co-)monad;

2. specifically

   1. $\flat \coloneqq Disc \circ \Gamma$ is the comonad induced from the terminal geometric morphism;

   2. ${{= loc_{\mathbb{R}^{0\vert 1}}} \atop {\phantom{A}}}$

      is the A1-localization at the superpoint;

3. each $L \dashv R$ denotes a pair of adjoint (∞,1)-functors;

4. each $F' \gt F$ means that $(F(X) \simeq X) \Rightarrow (F'(X) \simeq X)$.

$\,$

Moreover, with $\mathbf{H}$ also its

tangent (∞,1)-topos$T \mathbf{H}$ of parameterized spectrum objects in $\mathbf{H}$

inherits the same kind of progression.

$\,$

In conclusion

this progression of adjoint modalities

is the abstract reflection that inside $\mathbf{H}$

there is a good theory of

1. differential cohomology$\;\;$ $\int \dashv \flat \dashv \sharp$

2. differential geometry$\;\;$ $\Re \dashv \Im \dashv E\!t$

3. supergeometry$\;\;$ $\rightrightarrows \dashv \rightsquigarrow \dashv loc_{\mathbb{R}^{0\vert 1}}$

$\,$

Regarding the first point:

The $(\int \dashv \flat)$ fracture squares

$$\array{ && \int_{dR} {\hat E} && \stackrel{\phantom{AAAA}}{\longrightarrow} && \flat_{dR}{\hat E} \\ & \nearrow & & \searrow & & \nearrow && \searrow \\ \int_{dR} \flat {\hat E} && && {\hat E} && && \int \flat_{dR} \hat E \\ & \searrow & & \nearrow & & \searrow && \nearrow \\ && \flat {\hat E} && \underset{\phantom{AAA}}{\longrightarrow} && \int \hat E } \,.$$

exhibit each $\hat E \in T_\ast \mathbf{H}$ as a differential cohomology theory (Bunke-Nikolaus-Völkl 13)

$$\array{ && {{connection\;forms}\atop{on\;trivial\;bundles}} && \stackrel{de\;Rham\;differential}{\longrightarrow} && {{curvature}\atop{forms}} \\ & \nearrow & & \searrow & & \nearrow_{\mathrlap{curvature}} && \searrow^{\mathrlap{de\;Rham\;theorem}} \\ {{flat}\atop{differential\;forms}} && && {{geometric\;bundles}\atop{with\;connection}} && && {{rationalized}\atop{bundle}} \\ & \searrow & & \nearrow & & \searrow^{\mathrlap{topol.\;class}} && \nearrow_{\mathrlap{Chern\;character}} \\ && {{geometric\;bundles}\atop{with\;flat\;connection}} && \underset{comparison \;map}{\longrightarrow} && {{shape}\atop{of\;bundle}} }$$

(the differential cohomology hexagon).

$\,$

In particular if

the non-differential twisted generalized cohomology theory $E \coloneqq \int \hat E$ is prescribed

then a differential refinement $\hat E$ is obtained by

setting:

$$\array{ && \Omega_{flat}(-, \mathfrak{l}(E)) \\ & \nearrow && \searrow \\ \hat E && (pb) && E_{\mathbb{R}} \\ & \searrow && \nearrow \\ && E } \,,$$

where $\Omega(-,\mathfrak{l}(E))$ denotes the sheaf of flat super L-∞ algebra valued differential forms.

$\,$

The super $L_\infty$-cocycles discussed above are examples

of such flat super L-∞ algebra valued differential forms,

namely they are precisely the left invariant differential forms.

$\,$

Hence the above super L-∞ algebra is

the image under the Chern character of interesting

super twisted differential cohomology theory.

$\,$

Need to globalize this super-tangent space wise!

$\,$

To that end, consider the second stage of adjoint modalities $\Re \dashv \Im$

$\,$

Definition

Given $X,Y\in \mathbf{H}$ then a morphism $f \;\colon\; X\longrightarrow Y$ is a local diffeomorphism if its naturality square of the infinitesimal shape modality $\Im$

$$\array{ X &\longrightarrow& \Im X \\ \downarrow^{\mathrlap{f}} && \downarrow^{\mathrlap{\Im f}} \\ Y &\longrightarrow& \Im Y }$$

is a homotopy pullback square.

Definition

Given $X \in \mathbf{H}$, its infinitesimal disk bundle $T_{inf} X\to X$ is the pullback of the unit of the infinitesimal shape modality $\Im$ along itself

$$\array{ T_{inf} X &\stackrel{}{\longrightarrow}& X \\ \downarrow && \downarrow \\ X &\longrightarrow& \Im X } \,.$$

Definition

Let $V \in Grp(\mathbf{H})$ be an ∞-group.

A $V$-manifold is an $X \in \mathbf{H}$ such that there exists a $V$-atlas, namely a correspondence of the form

$$\array{ && U \\ & {}^{\mathllap{et}}\swarrow && \searrow^{\mathrlap{et}} \\ V && && X }$$

with both morphisms being local diffeomorphisms, def. , and the right one in addition being an epimorphism, hence an atlas.

Proposition

(Khavkine-Schreiber 17, Wellen 17)

For $X$ a $V$-manifold, def. , then its infinitesimal disk bundle $T_{inf} X \to X$, def. , is associated to a $GL(V)$-principal $Fr(X) \to X$ – to be called the frame bundle, modulated by a map to be called $\tau_X$, producing homotopy pullbacks of the form

$$\array{ T_{inf} X &\longrightarrow& V/GL(V) \\ \downarrow && \downarrow \\ X &\stackrel{\tau_X}{\longrightarrow}& \mathbf{B} GL(V) } \;\;\phantom{AAAAA}\; \array{ Fr(X) &\longrightarrow& \ast \\ \downarrow && \downarrow \\ X &\stackrel{\tau_X}{\longrightarrow}& \mathbf{B} GL(V) } \,.$$

$\,$

This provides all the ingredients

to incarnate super topological T-duality globally

in terms of twisted super-differential cocycles on super-stacks

that tangent complex-wise restrict to the above super $L_\infty$-cocycle models.

$\,$

To be done.

$\,$

References

Detailed pointers to the literature are contained in the above text.

Here we only list the references to the original work reported on here.

$\,$

Our discussion of L-infinity algebra cohomology is due to

• Hisham Sati, Urs Schreiber, Jim Stasheff, L-infinity algebra connections and applications to String- and Chern-Simons n-transport, in Quantum Field Theory, Birkhäuser (2009) 303-424 (arXiv:0801.3480)

The observation of the brane bouquet in super $L_\infty$-algebra and the general construction of higher WZW terms from higher $L_\infty$-cocycles is due to

• Domenico Fiorenza, Hisham Sati, Urs Schreiber, Super Lie n-algebra extensions, higher WZW models and super p-branes with tensor multiplet fields International Journal of Geometric Methods in Modern Physics Volume 12, Issue 02 (2015) 1550018, (arXiv:1308.5264)

The homotopy-descent of the M5-brane cocycle and of the type IIA D-brane cocycles is due to

• Domenico Fiorenza, Hisham Sati, Urs Schreiber, The WZW term of the M5-brane and differential cohomotopy, J. Math. Phys. 56, 102301 (2015) (arXiv:1506.07557)

• Domenico Fiorenza, Hisham Sati, Urs Schreiber, Rational sphere valued supercocycles in M-theory, Journal of Geometry and Physics, Volume 114 (2017) (arXiv:1606.03206)

The derivation of supersymmetric topological T-duality, rationally, and of the higher super Cartan geometry for super T-folds is due to

• Domenico Fiorenza, Hisham Sati, Urs Schreiber, T-Duality from super Lie n-algebra cocycles for super p-branes, ATMP 2018 (arXiv:1611.06536)

The derivation of the process of higher invariant extensions that leads from the superpoint to 11-dimensional supergravity:

• John Huerta, Urs Schreiber, M-Theory from the Superpoint (arxiv:1702.01774)

General discussion of twisted cohomology is in

• Thomas Nikolaus, Urs Schreiber, Danny Stevenson, Principal ∞-bundles – General theory, Journal of Homotopy and Related Structures, Volume 10, Issue 4 (2015) (arXiv:1207.0248)

The rational homotopy theory of parameterized spectra is discussed in

• Vincent Schlegel, Urs Schreiber Rational parameterized stable homotopy theory, (thesis Schlegel)

The synthetic differential Cartan geometry is discussed in

• Igor Khavkine, Urs Schreiber, Synthetic geometry of differential equations, Part I. Jets and comonad structure (arXiv:1701.06238, v2, talk video)

• Felix Wellen, Formalizing Higher Cartan Geometry in Modal Homotopy Type Theory, PhD Thesis (in preparation) HoTT-Agda code: DCHoTT-Agda.

A textbook account of some of the story is in

• Urs Schreiber, differential cohomology in a cohesive topos, Thesis

---

$\,$