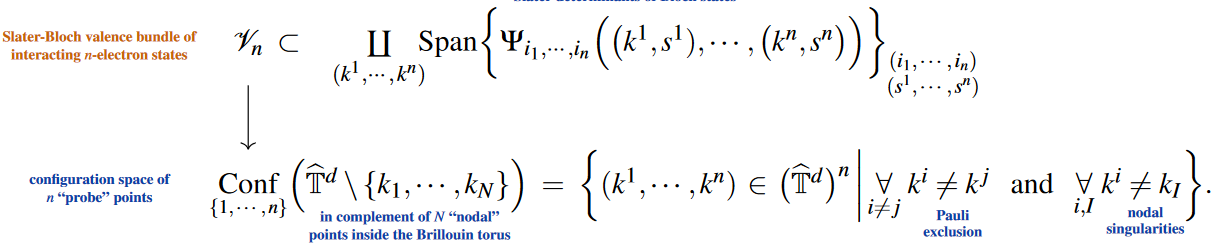Schreiber Towards Certified Topological Quantum Programming via Linear Homotopy Types
A talk that I have given:
-
Towards
Certified Topological Quantum Programming
via Linear Homotopy Types
talk at:
Quantum Information and Quantum Matter 2024,
NYU Abu Dhabi, 27-31 May 2024
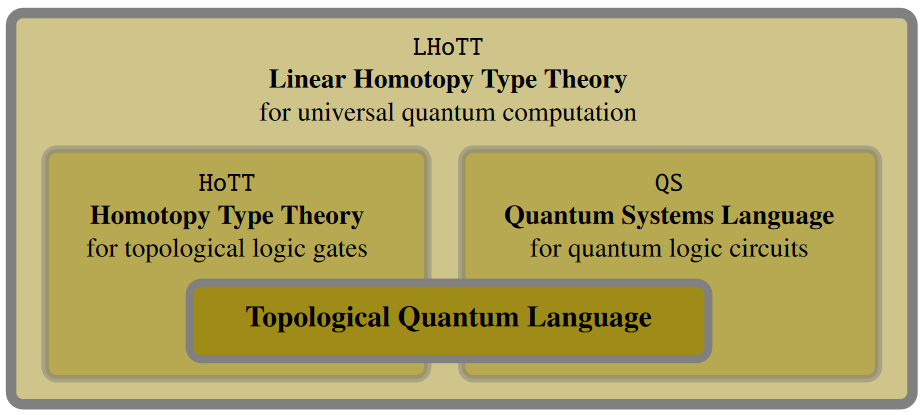
Abstract. Beyond the present NISQ era, useful heavy-duty quantum programs will arguably necessitate (1.) topological quantum circuits for error-protection and (2.) (classical-)computer-verified certificates of correctness — hence essentially a formal verification logic of the underlying topological quantum processes — which may seem a tall order. But we have recently shown that the (conservative) extension of the (programming & certification-)language of “Homotopy Type Theory” (
HoTT) by “linear homotopy types” (LHoTT, for which prototypes exist on paper) namely: by classically-controlled topological quantum data types, naturally lends itself to just this purpose. In this talk I will give an introduction to and survey of this approach to Topological Quantum Programming Certification via Linear Homotopy Types, developed at CQTS @ NYUAD (“Topological Quantum Gates in HoTT” arXiv:2303.02382, “Entanglement of Sections” arXiv:2309.07245, “The Quantum Monadology” arXiv:2310.15735, “Quantum and Reality” arXiv:2311.11035).
Contents
Talk Script
Motivation and Overview
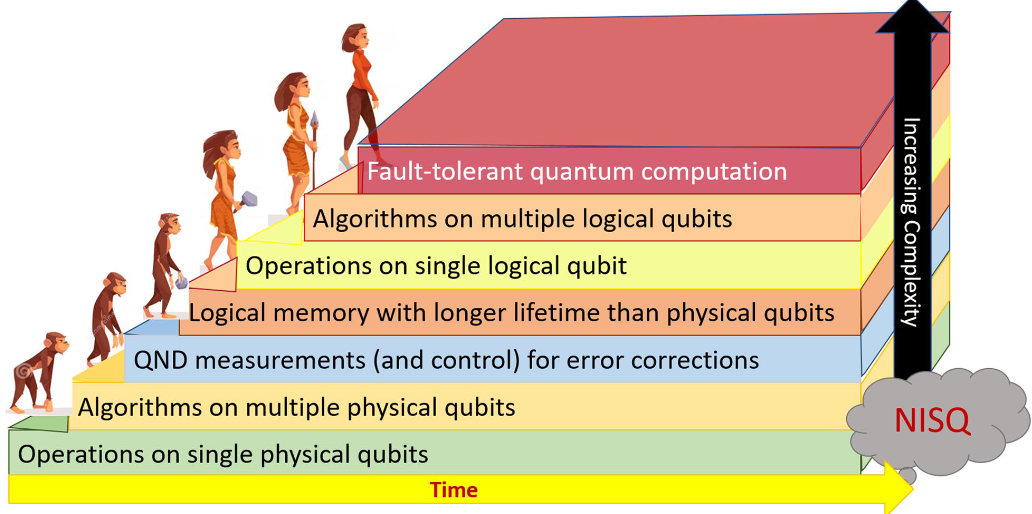
In the current
Noisy Intermediate Quantum (NISQ) era
we see that quantum computing works
in principle — namely in small-scale examples
(cf. quotes here)
Towards the anticipated
the remaining problem is:
To get it under control,
to scale up to heavy-duty usefulness.
(cf. quote here)
If we allow ourselves to step back and re-examine
the long-term perspective of heavy-duty quantum
we see that the following
basic problems have remained unsolved:
-
of the quantum hardware by topological quantum error protection
(cf. quotes here)
-
of qbit quantum circuits into the available topological quantum gates

-
of the resulting (topological) quantum protocols at compile-time
by formal proof — since de-bugging ceases to be an option
(cf. quotes here)
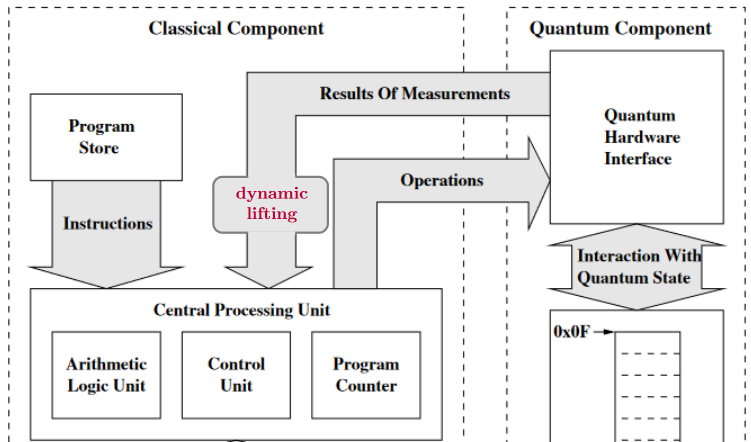
where all of this must be subject to
-
of the quantum system by classical control
including dynamic lifting of quantum measurement
notably for quantum error correction
(cf. quotes here)
We may observe that these are largely
issues of theory, of formal language:
-
theory of topological phases of quantum matter
has arguably remained shaky
(cf. the experimentally elusive MZMs)
-
nature of topological quantum gates
had not been reflected in existing quantum programming languages
-
formal methods for verifying classical code
had not been thoroughly adapted to quantum
(in particular because quantum identity types had been missing – but see below)
-
theory of classically dependent quantum data types
had not been satisfactorily developed
(cf. quote here)
We may also observe that
solving this looks like a hard problem
for a reason:
Quantum certification language is Formal quantum theory.
To properly verify a (topological) quantum program,
the verification language needs to accurately
reflect key aspects of actual quantum physics
thus effectively being a formal theory of quantum systems
(which is how we originally arrived here: S. 2014a, S. 2014b).
It may seem a tall order to formalize all this.
And yet:
Our claim is that a miracle occurs (explained below):
any extension of “homotopically typed” languages
by linear homotopy types which satisfy
an axiom scheme called the Motivic Yoga
as anticipated in: arXiv:1402.7041 pp. 39
prototyped on paper in: doi:10.14418/wes01.3.139
provides a formal context in which
such topological quantum language
may admissibly be embedded
as laid out in:
“Topological Quantum Gates in HoTT” arXiv:2303.02382,
“Entanglement of Sections” arXiv:2309.07245
Next to explain a little what this means.
Data Types and Spaces
The simple but profound idea of program verification is
to always declare the data type of any datum
specifying what the data may be
and how it may be be used.
For example, in modeling the quantum Hall effect
one needs to specify the numerical datum “”.
If one declares this to be a real number
then an irrational value like
would conform to the data type specification while
violating the intended meaning of the program.
But if one instead declared the datum to be a rational number
as befits discussion of the fractional quantum Hall effect,
then an ill-identification like
can be recognized as an error at compile-time.
In this vein, if one declared even more restrictively
the data to be an integer number
then the code would be verified (“type checked”)
when appropriate for the integer quantum Hall effect.
Simple as it is, carrying this
idea of thorough data typing
to all its logical implications
yields remarkably expressive languages.
This is the topic of type theory.
In particular a program is what maps
data of specified input type to
data of specified output type
The goal then is
to form data types
such that a datum is iff
it conforms to its intended specification
so that a program is verified iff it can be
guaranteed to produce data of type .
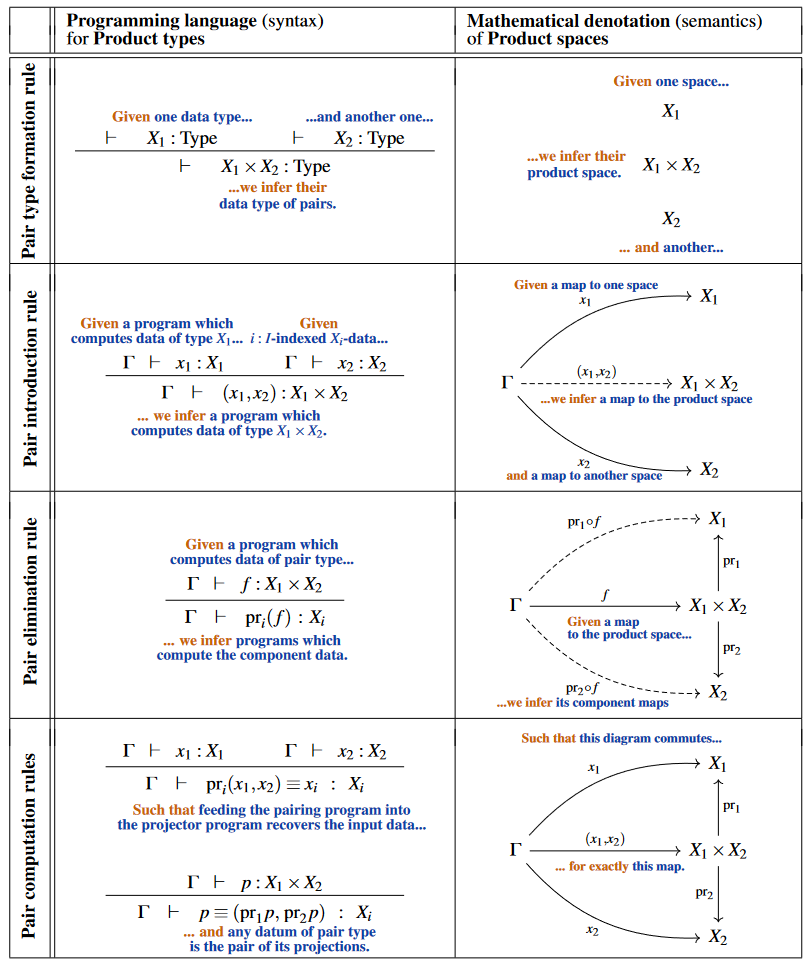
For example, given data types , we may
form the new type of pairs of data
with and ,
which is defined by the following inference rules
prescribing how to form valid data from given data
(shown here just to give an impression):
What this means is that a program which
outputs data of such pair type
is guaranteed to produce valid data,
obeying the logical rule that there is
an -datum and an -datum.
By further such elementary type formation rules
one may specify and verify any logical constraint on data
a fact known by the slogan “propositions are types”.
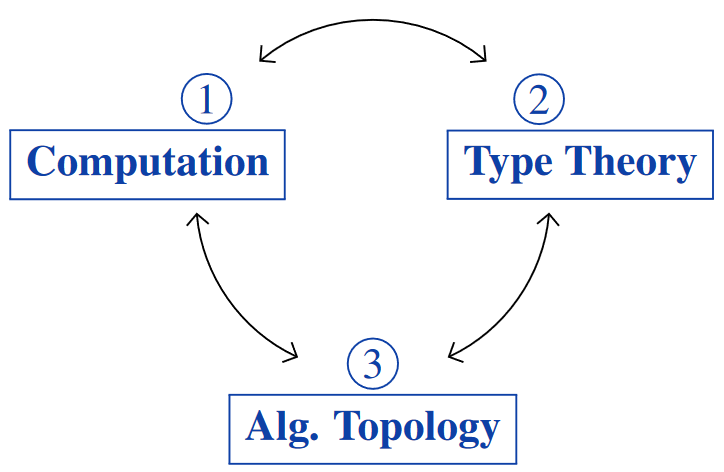
This has a remarkable analogy with topology:
The defining properties of the above pair types
are just those of topological product spaces.
More precisely and yet more generally, this has
a remarkable analogy with algebraic topology:
The defining properties of such pair types
are just the universal properties
of category theoretic product objects.
This confluence of concepts between
has been called the computational trilogy.
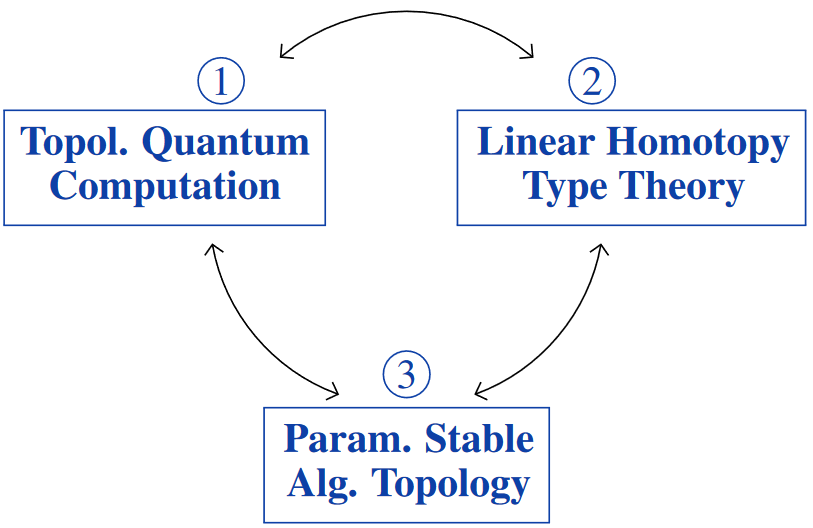
Our basic observation [Sati S. 2022] may be summarized as:
there is a natural quantum enhancement of the trilogy to
a topological quantum computational trilogy between
which reveals a natural solution to the above
problem of topological quantum certification.
To this end, consider next the situation
where the type of a datum actually depends
on given data
For example the dimension of a Hilbert space
which serves as the data type of a quantum state
may depend on previous computations:
Now,
taking the principle of data typing fully seriously,
it should be applied also to identifications of data:
Suppose a program is to compute certificates that
pairs of data may be identified (“are equal”).
For example
-
may be the computed output of a quantum circuit
and the intended output
then certifying is to verify
the correct implementation of the protocol.
(cf. Riley 2022)
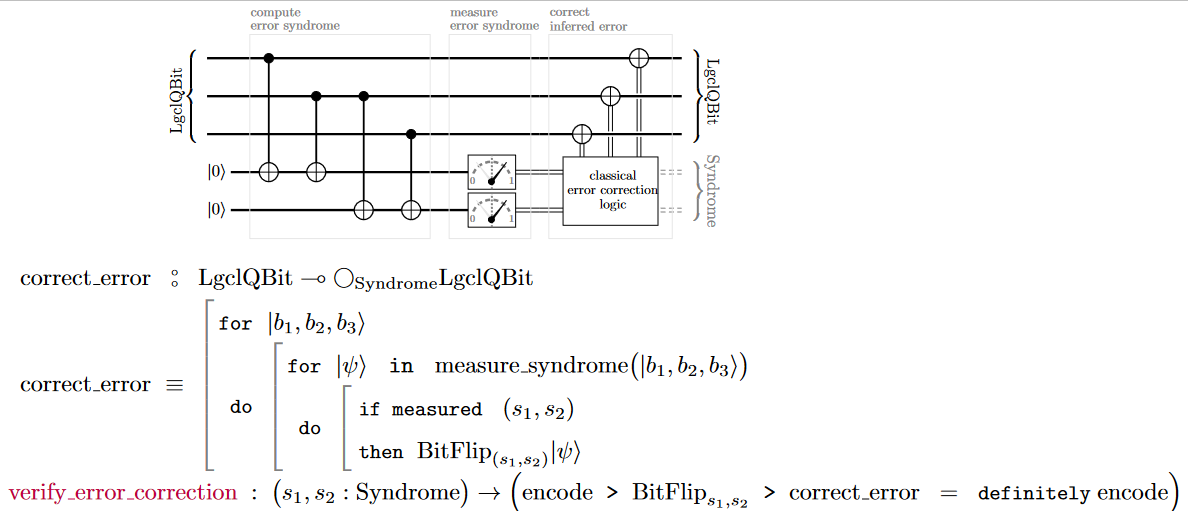
-
may be the output of a noisy channel followed by error correction
while is the output of the undisturbed channel, then
verifying the correctness of the error-correction protocol
is to produce a certificate that
shown here for the bit flip code:
But then also these id-certificates need to have a data type
called identification type (or “identity type”)
By a most remarkable development in computer science
the foundational insight of homotopy type theory is
that the semantics of such identification types
is that of path space fibrations in topology.
Indeed, their inference rules correspond to
(“parallel”) transport in (Serre-)fibrations
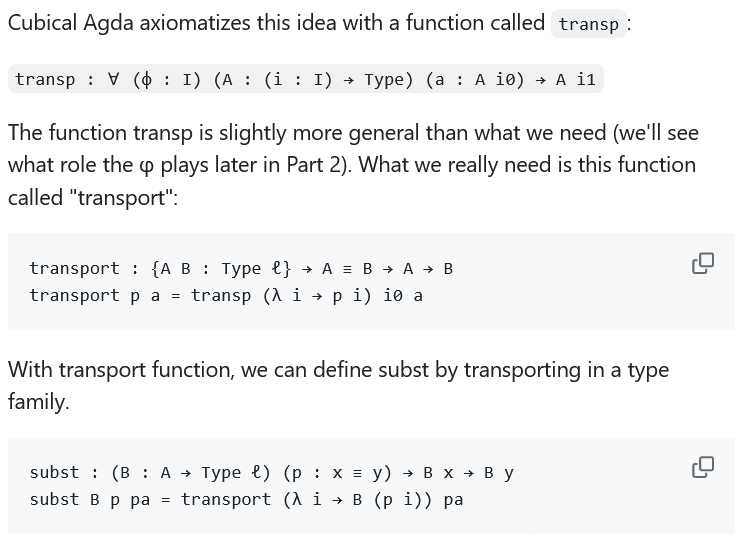
Hence in homotopy-typed programming languages like Cubical Agda
the seemingly sophisticated notion of parallel transport in fibrations
is a native expression in the programming language.
(code snippets from Myers & Riley 2023)
Quantum and Topology
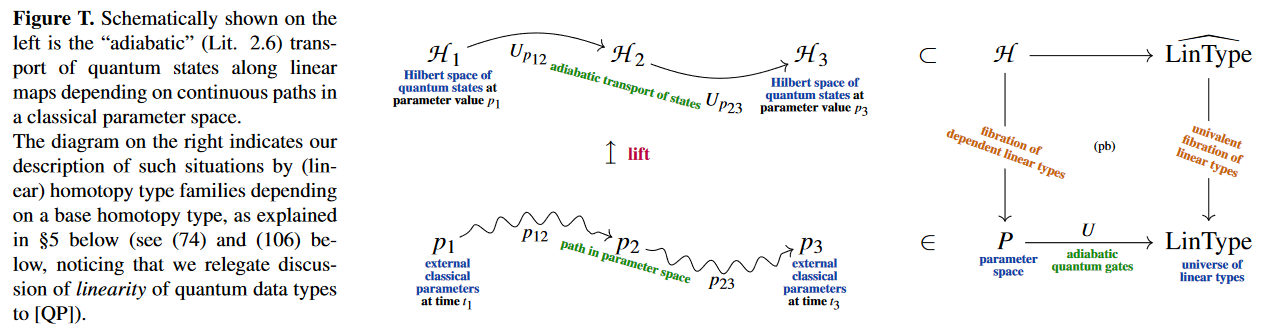
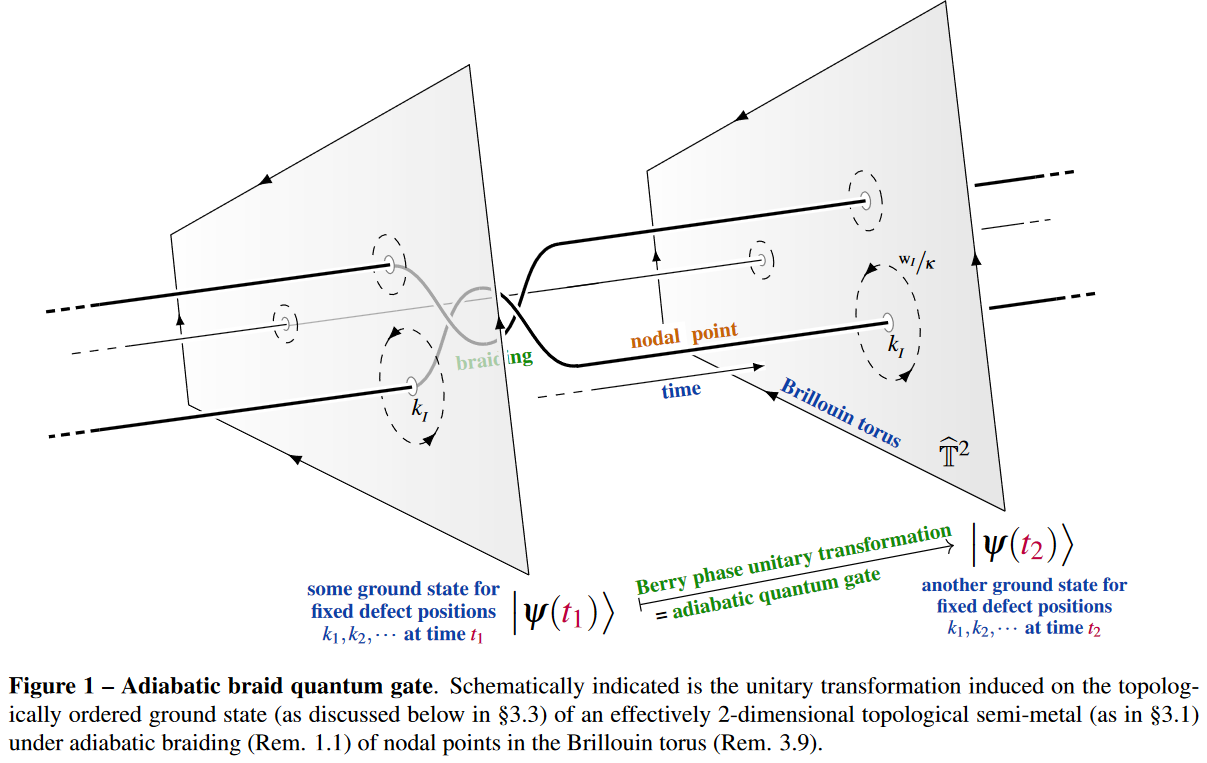
The key point for us now is, as we may observe, that:
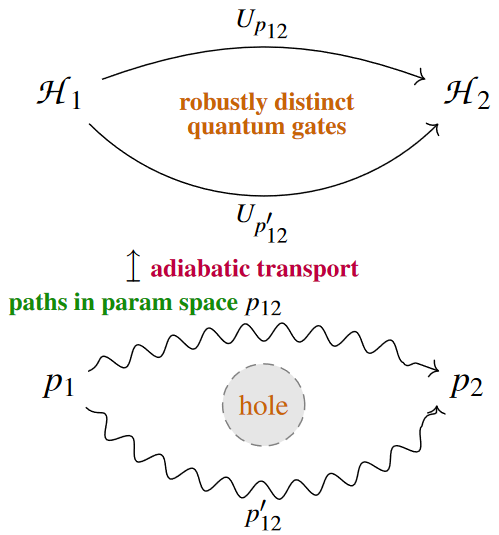
quantum adiabatic evolution is an example of such transport
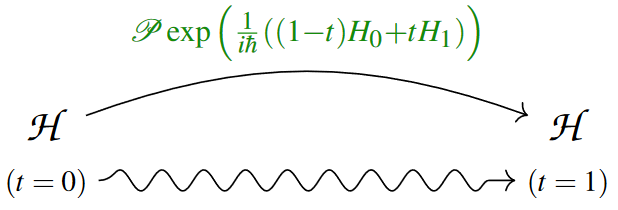
A simple special case is quantum annealing
where there is an essentially unique parameter path:
A more profound special case is holonomic quantum computation
where there are non-contractible paths in parameter space
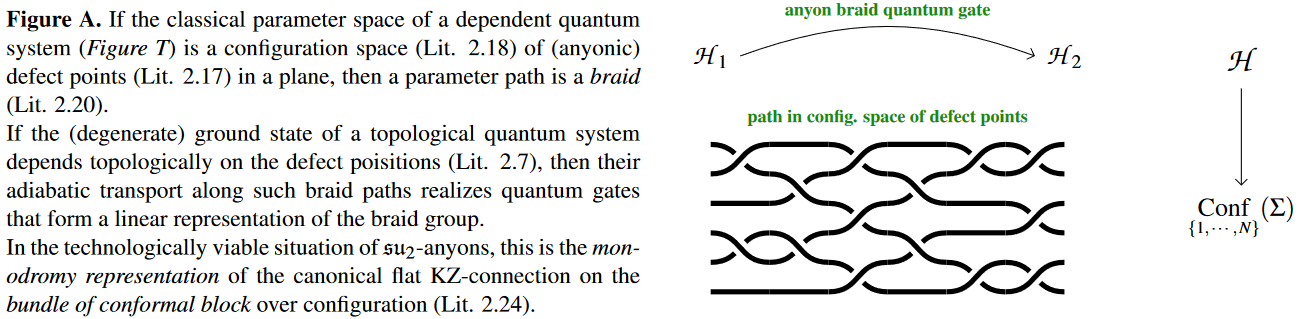
In particular anyon braid gates
for topological quantum computation
are of such a form:
This suggests that
thoroughly data-typed (namely: homotopically typed) programming languages
may natively know about
(the algebraic topology underlying) topological quantum computation.
In fact, we may observe that fundamentally
not only topological quantum gates but
all real quantum gates are continuous paths in parameter space:
Therefore having
path lifting as a native expression of a language
goes a long way in quantum computation.
The theorem: Anyon language
Still, the expected physics of anyon braid gates is rich:
For -anyons (Majorana-, Fibonacci-…)
the Laughlin wavefunctions of ground states of topologically ordered quantum materials
are identified with the conformal blocks of -current algebra 2d conformal quantum field theory
and their braiding is described by the Knizhnik-Zamolodchikov equation on
the vector bundle of conformal blocks over the configuration space of anyon defect positions.
Can a homotopically typed language really natively speak about —
and hence verify — the actual specification of such gates?
Yes!
That this is indeed the case is the main theorem of
- Myers, Sati & S.: Topological Quantum Gates in Homotopy Type Theory, CMP (2024)
based on the K-theoretic re-analysis of anyons in
-
Sati & S.: Anyonic defect branes in TED K-theory, RMP (2023)
-
Sati & S.: Anyonic topological order in TED K-theory, RMP (2023)
Schematically the proof procedes as follows:
braiding of
Laughlin wavefunctions of —Quantum Field Theory—
(KZ-connection on -conformal blocks)
twisted cohomology of —Algebraic Topology—
(hypergeometric WZW construction)
0-truncated function types into —Homotopy Type Theory—
Side remark on solid state physics:
Here the first equivalence was found [Sati S. 2023] in the process of
generalizing the K-theory classification of topological phases of matter
from free to interacting topological phases
by passing
from K-theory of the Brillouin torus-orbifold — classifying single-electron states
to K-theory of its configuration space of points — classifying multi-electron Slater-det states.
Namely the twisted de Rham cohomology in the above theorem
is secretly the Chern character on this equivariant K-theory
In conclusion, this suggests that there ought to be a natural encoding
of topological braid quantum gates into homotopy typed languages.
And indeed there is –
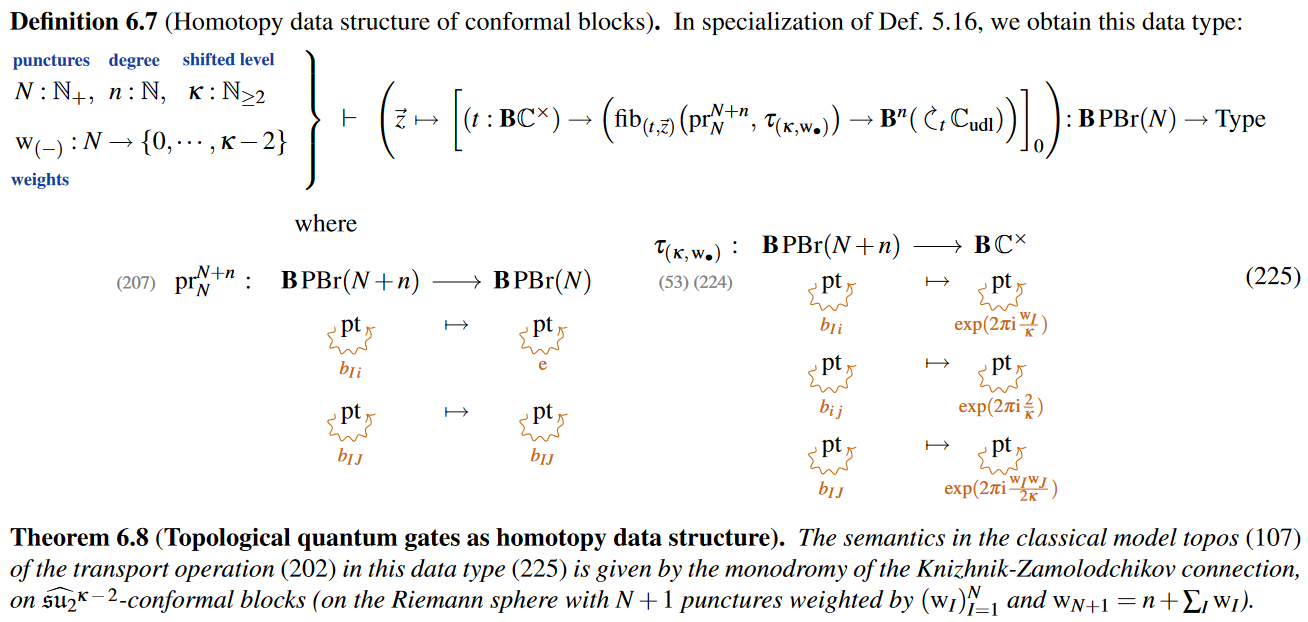
it fits on one line [Myers, Sati and S. 2024, Thm. 6.8]:
This is currently being implemented in Cubical Agda by D. J. Myers et al. @ CQTS.
Quantum Data and Linear Spaces
The only aspect missing up to this point
is the specification of these types of (topological) quantum states
as linear spaces (Hilbert spaces) hence as linear types
equipped with a tensor product modelling their quantum entanglement
Formally, the “quantum-ness” of the tensor product of quantum state spaces
rests in the fact that it is not cartesian.
Namely the cartesian product of classical state spaces
(by its defining universal property)
comes with natural projection and with diagonal maps
corresponding to deletion and copying of classical data
reflected syntactically in structural rules called
the weakening rule and contraction rule:
Famously (known as the no-cloning theorem and no-deleting theorem)
these operations do not naturally exist on quantum state spaces.
Hence for quantum data types these structural inference rules
are to be omitted. The resulting substructural types are known as linear types:
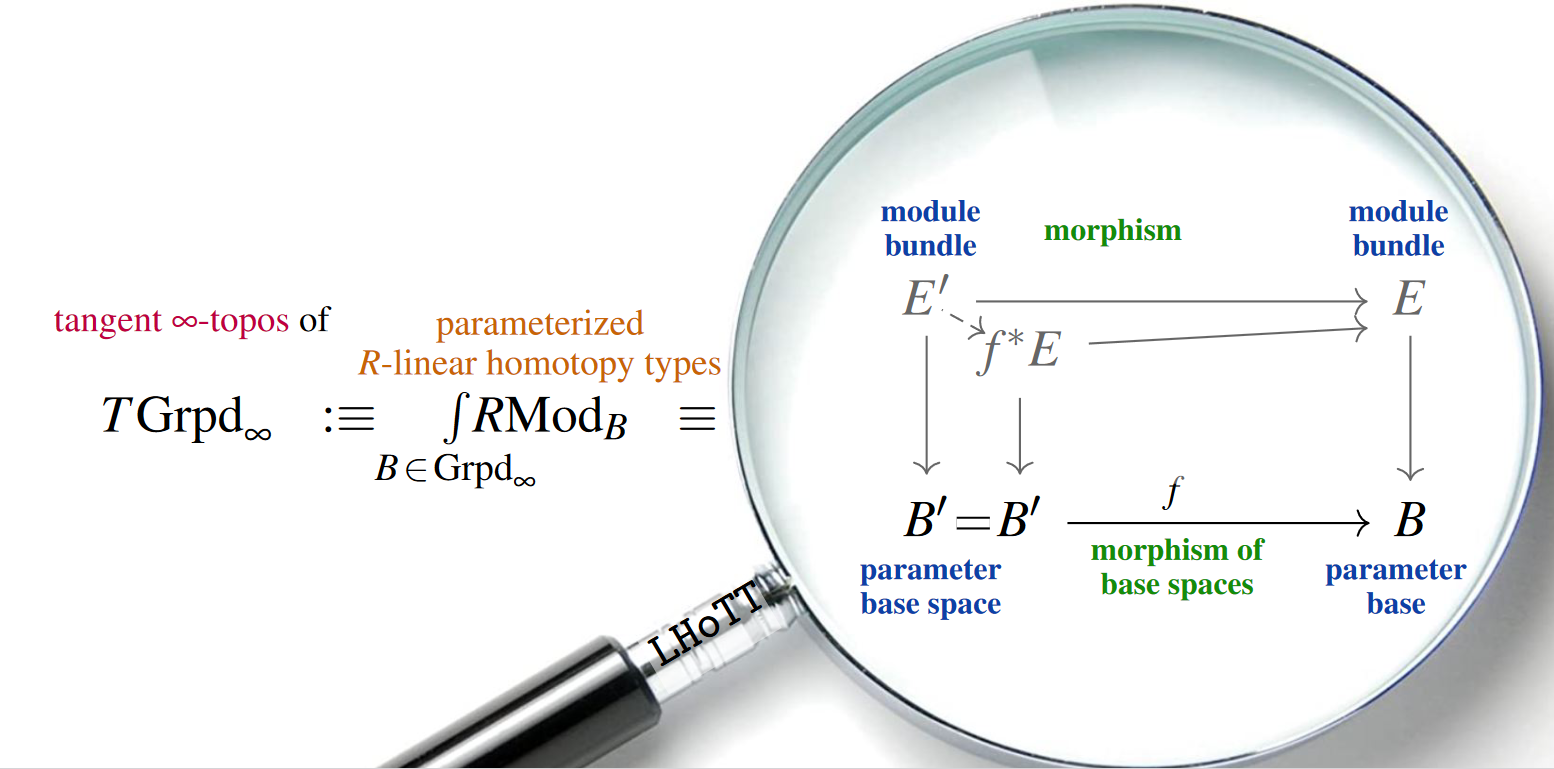
That there ought to be an extension
of homotopy typed languages
we anticipated in Quantization via Linear Homotopy Types [arXiv:1402.7041]
motivated by high energy quantum physics [FormalMath@IHP 2014].
A proto-type was produced by Riley 2022.
What makes this work, semantically,
is a deep surprising theorem in modern algebraic topology
which roughly says – echoing Bohr’s famous standpoint:
- Topologicalquantum logic, when parameterized, becomes a form of classical logic.
[highlighted in FormalMath@IHP 2014, Prop. 2.5, p. 6]
This embeds the above encoding of anyon braid gates
into a fully-fledged quantum certification environment
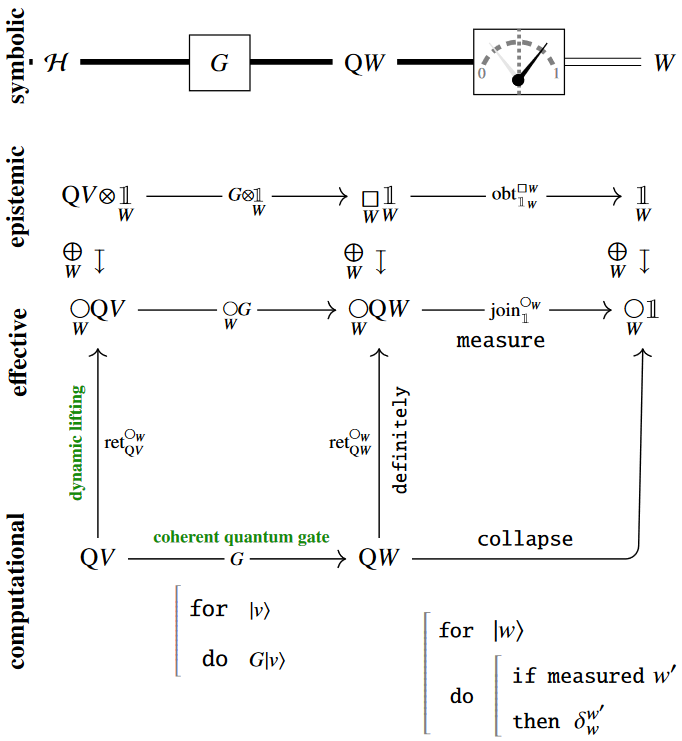
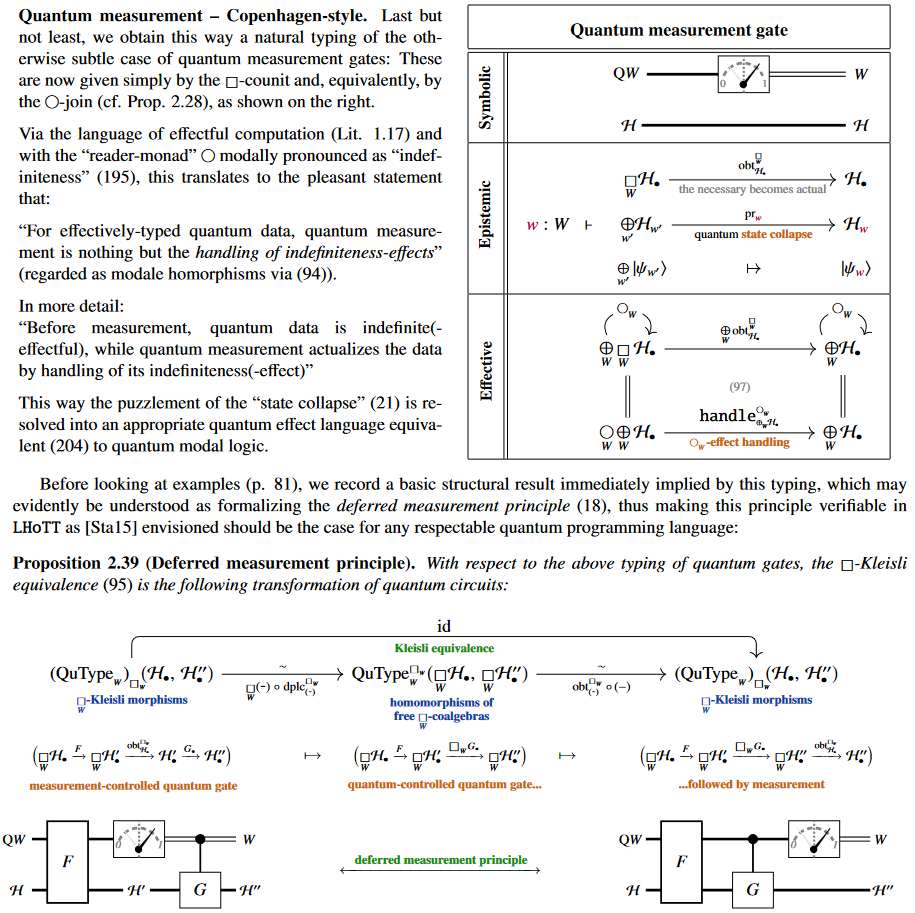
which can naturally verify basic quantum principles
such as the deferred measurement principle
Outlook. We have established an approach to the
general problem of topological quantum certification languages
of the following form
which seems practically promising and theoretically intriguing.
Much work remains to further flesh this out
and eventually implement it on computers.
Related presentations
-
(upcoming) Topological Quantum Programming via Linear Homotopy Types,
talk at Quantum Physics and Logic 2024, Buenes Aires, 15-19 July 2024
-
Towards Quantum Programming via Linear Homotopy Types,
talk at Homotopy Type Theory and Computing – Classical and Quantum,
CQTS @ New York University Abu Dhabi, 19-21 April 2024
-
Topological Quantum Programming via Linear Homotopy Types
talk at: Homotopy Type Theory Electronic Seminar (01 Feb 2024)
-
Effective Quantum Certification via Linear Homotopy Types,
talk at Colloquium of the Topos Institute
Part I: 13 April 2023 [video: YT, slides:pdf]
Part II: 24 Aug 2023 [video:YT, slides:pdf]
-
Towards verified topological hardware-aware quantum programming
talk at CQTS & TII Workshop 2023, CQTS @ NYU Abu Dhabi, 24 Feb 2023
[slides:pdf]
-
Topological Quantum Programming in
TED-Ktalk at PlanQC 2022 33 (15 Sep 2022)
-
Quantum Data Types via Linear Homotopy Type Theory
talk at Workshop on Quantum Software @ QTML 2022, Naples, 12 Nov 2022
[slides: pdf]
Last revised on October 31, 2024 at 09:02:34. See the history of this page for a list of all contributions to it.