nLab quantum error correction
Context
Quantum systems
-
quantum algorithms:
Computation
constructive mathematics, realizability, computability
propositions as types, proofs as programs, computational trinitarianism
Constructive mathematics
Realizability
Computability
Contents
Idea
General
Quantum error correction is concerned with ensuring the robustness of quantum computation against noise (as in classical error correction) and particularly against quantum noise and quantum decoherence (e.g. against bit flip errors).
From Ferris & Poulin 2013:
The basic principle of quantum error correction (QEC) is to encode information into the long-range correlations of entangled quantum many-body states in such a way that it cannot be accessed locally. When a local error affects the system, it leaves a detectable imprint—called the error syndrome. The decoding problem consists in inferring the recovery with greatest probability of success given the error syndrome. In general, this is a hard problem, but for well-chosen codes, it can be solved efficiently either exactly or heuristically.
From Steane 06:
Error correction is especially important in quantum computers, because efficient quantum algorithms make use of large scale quantum interference, which is fragile, i.e. sensitive to imprecision in the computer and to unwanted coupling between the computer and the rest of the world. This makes large scale quantum computation so difficult as to be practically impossible unless error correction methods are used. Indeed, before quantum error correction was discovered, it seemed that this fragility would forbid large scale quantum computation. The ability to correct a quantum computer efficiently without disturbing the coherence of the computation is highly non-intuitive, and was thought more or less impossible. The discovery of powerful error correction methods therefore caused much excitement, since it converted large scale quantum computation from a practical impossibility to a possibility.
From Devitt, Nemoto & Munro 2009:
Starting in 1995, several papers appeared, in rapid succession, proposing codes which were appropriate to perform error correction on quantum data (Sho95; Ste96a; CS96; LMPZ96; BSW96). This was a key theoretical development needed to convince the general community that quantum computation was indeed a possibility. Since this initial introduction, the progress in this field has been extensive.
From Zhu & Cross 20:
Although we are currently in an era of quantum computers with tens of noisy qubits, it is likely that a decisive, practical quantum advantage can only be achieved with a scalable, fault-tolerant, error-corrected quantum computer. Therefore, development of quantum error correction is one of the central themes of the next five to ten years.
Within the decade, Google aims to build a useful, error-corrected quantum computer. Our journey to build an error-corrected quantum computer within the decade includes several scientific milestones, including building an error-corrected logical qubit.
Specifically on holographic quantum error correcting codes (see references below):
From Harlow 20:
The codes provided by AdS/CFT often come close to saturating theoretical bounds on the performance of quantum codes. It seems AdS/CFT may be a tool for discovering better quantum cryptography?
holographic codes could be promising candidates to circumvent our results and could possibly realise a universal set of unitary implementations of logical operators.
From CDCW 21:
There are a number of reasons to suspect that holographic codes may be of practical use for quantum computing.
Holographic codes can admit erasure thresholds comparable to that of the widely-studied surface code, and likewise for their threshold against Pauli errors. Their holographic structure also naturally leads to an organization of encoded qubits into a hierarchy of levels of protection from errors, which could be useful for applications which call for many qubits withvarying levels of protection. In particular, this is reminiscent of many schemes for magic state distillation – and indeed, the concatenated codes utilized for magic state distillation share a similar hierarchical structure to holographic codes. The layered structure of holographic codes is also reminiscent of memory architectures in classical computers, where it is useful to have different levels of short- and long-term memory. Although these codes have some notable drawbacks, in particular holographic stabilizer codes require nonlocal stabilizer generators, other codes such as concatenated codes suffer similar drawbacks and have still proven to be useful. Conversely, the stringent requirement of non-local stabilizer generators allows holographic codes to protect many more qubits than a topological code and in fact attain a finite nonzero encoding rate, which is typically not possible for topological codes. Nonetheless, many open questions remain about the usefulness of holographic codes for fault-tolerant quantum computing.
Quantum error correcting codes
The simple but important special case of passive correction of erasures may be handled by quantum error correcting codes:
Recall that a classical error correcting code on a finite set of states is, typically, a choice of injection of into some larger set, typically a Cartesian power
(often considered in the form of linear codes, but classical nonetheless). In quantum physics the Cartesian product of sets of states is replaced by the tensor product of Hilbert spaces.
For a given Hilbert space of quantum states (finite-dimensional in practice), a quantum error correcting code is a choice of linear embedding (the code subspace) of into a larger Hilbert spaces, often an -fold tensor product of copies of some :
such that the information in in some of the tensor factors can be lost without obstructing the reconstruction of (e.g. Rowell & Wang 17, Sec. 3.2.3).
(Often one demands additional properties, such as that a given set of linear operators (quantum observables) acting on are implemented on by combinations of operators that act non-trivially only on some of the tensor factors.)
While this is superficially analogous to a classical error correcting code, the crucial and subtle difference is that quantum error correction codes thus take place in a non-Cartesian symmetric monoidal category. For this reason, effects of quantum entanglement play a paramount role in quantum error correction codes.
Example
Specific examples
Bit flip codes
See at bit flip code.
A 3-qutrit code
The following is a simple illustrative example from Cleve, Gottesman & Lo 99, p. 1-2:
Consider a quantum system with a 3-dimensional space of quantum states:
and consider a code space inside 3 copies of this space given by the following linear map
This code corrects errors consisting of the loss of one of the three copies, in the following sense:
There is a linear operator acting only on two of the three copies, explicitly given (ADH 14 (3.6)) by
such that
The HaPPY code
The HaPPY code is a quantum error correction code (a class of such codes really, indexed by a “cutoff” natural number) which is thought to exhibit characteristic properties akin to the encoding of bulk-quantum states by boundary-states expected in the AdS/CFT correspondence. In particular, the HaPPY code (or rather the tensor network that defines it) exhibits a discretized form of the Ryu-Takayanagi formula for holographic entanglement entropy.
Concretely, the the HaPPY code subspace is the image of the linear map formed by:
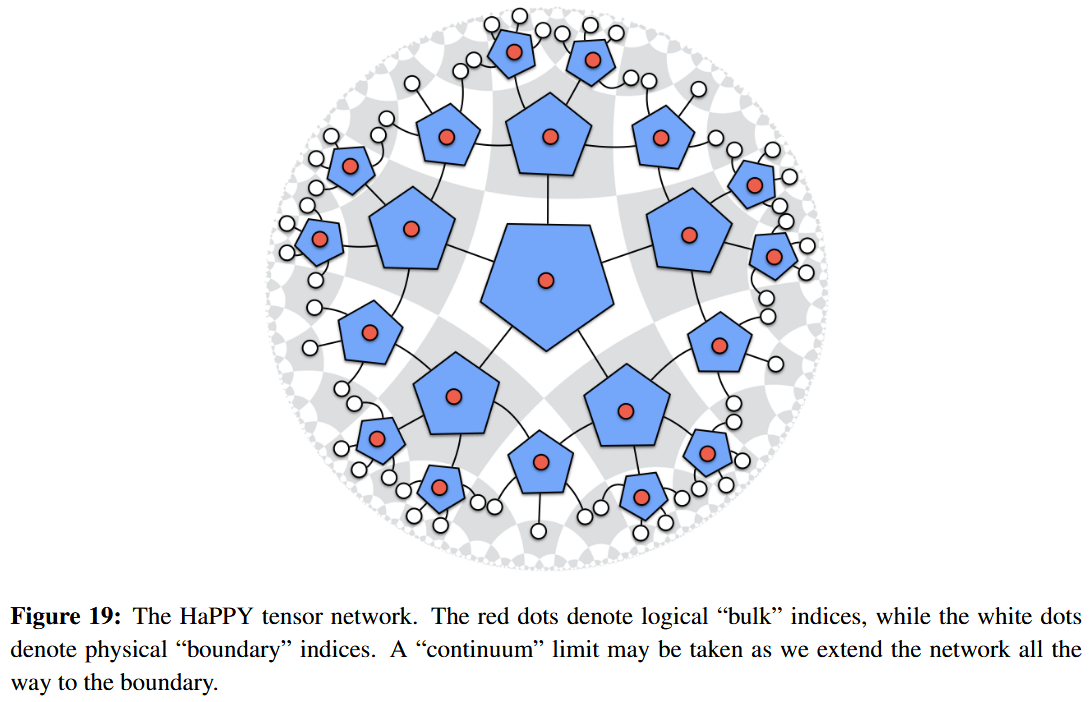
-
picking a perfect tensor of rank 6;
-
picking a finite cutoff of the pentagonal tesselation of the hyperbolic plane;
-
regarding its Poincaré dual graph as a tensor network (string diagram in finite-dimensional vector spaces) by
-
regarding the uncontracted edges at the cutoff boundary as output (shown in white)
and thus as a linear map from the tensor product over the bulk-vertices to the tensor product over the edges sticking out over the boundary.
Majorana dimer codes
See at Majorana dimer code.
Classes of examples
Related concepts
References
General
The idea of quantum encryption based on the no-cloning theorem originates with:
- Stephen Wiesner, Conjugate Coding, circulated in the 1960s, finally published in ACM SIGACT News 15 1 (1983) 78–88 (original pdf, doi:10.1145/1008908.1008920)
Original articles on quantum error correcting codes:
-
Peter W. Shor, Scheme for reducing decoherence in quantum computer memory, Phys. Rev. A 52, R2493(R) 1995 (doi:10.1103/PhysRevA.52.R2493)
-
Andrew M. Steane, Error Correcting Codes in Quantum Theory, Phys. Rev. Lett. 77, 793 1996 (doi:10.1103/PhysRevLett.77.793)
-
Robert Calderbank, Peter W. Shor, Good Quantum Error-Correcting Codes Exist, Phys. Rev. A, Vol. 54, No. 2, pp. 1098-1106, 1996 (doi:10.1103/PhysRevA.54.1098)
-
Raymond Laflamme, Cesar Miquel, Juan Pablo Paz, Wojciech H. Zurek, Perfect Quantum Error Correction Code, Phys. Rev. Lett., 77:198, 1996 (arXiv:quant-ph/9602019)
-
Charles H. Bennett, David P. DiVincenzo, John A. Smolin, William K. Wootters, Mixed State Entanglement and Quantum Error Correction, Phys. Rev. A54:3824-3851, 1996 (doi:10.1103/PhysRevA.54.3824)
-
Andrew M. Steane, Multiple Particle Interference and Quantum Error Correction, Proc. Roy. Soc. Lond. A452 (1996) 2551 (arXiv:quant-ph/9601029)
-
Emanuel Knill, Raymond Laflamme, A Theory of Quantum Error-Correcting Codes, Phys. Rev. Lett. 84:2525-2528, 2000 (arXiv:quant-ph/9604034)
Realization that quantum error correcting codes could make quantum computation practically feasible (quantum error threshold theorem):
-
Emanuel Knill, Raymond Laflamme, Wojciech H. Zurek, Resilient Quantum Computation: Error Models and Thresholds, Proceedings of the Royal Society A 454 1969 (1998) [arXiv:quant-ph/9702058]
-
John Preskill, Fault-tolerant quantum computation, in: Introduction to Quantum Computation and Information, World Scientific (1998) arXiv:quant-ph/9712048, doi:10.1142/3724
-
John Preskill, Reliable Quantum Computers, Proc. Roy. Soc. Lond. A 454 (1998) 385-410 arXiv:quant-ph/9705031, doi:10.1098/rspa.1998.0167
-
Daniel Gottesman, Theory of fault-tolerant quantum computation, Phys. Rev. A 57 (1998) 127-137 doi:10.1103/PhysRevA.57.127
-
Dorit Aharonov, Michael Ben-Or, Fault-Tolerant Quantum Computation With Constant Error Rate, SIAM J. Comput., 38 4 (2008) 1207–1282 [arXiv:quant-ph/9906129, doi:10.1007/978-3-642-32512-0_31]
-
Daniel Gottesman, Fault-Tolerant Quantum Computation, Physics in Canada 63 4 (2007) 183-189 arXiv:quant-ph/0701112
-
Dorit Aharonov, Michael Ben-Or, Fault-Tolerant Quantum Computation With Constant Error Rate, SIAM J. Comput. 38 4 (2008) 1207–1282 (arXiv:quant-ph/9906129, doi:10.1137/S0097539799359385)
-
Panos Aliferis, Daniel Gottesman, John Preskill, Quantum accuracy threshold for concatenated distance-3 codes, Quant. Inf. Comput. 6 (2006) 97-165 (arXiv:quant-ph/0504218)
-
Earl T. Campbell, Barbara M. Terhal, Christophe Vuillot: Roads towards fault-tolerant universal quantum computation, Nature 549 (2017) 172–179 doi:10.1038/nature23460
Operator algebraic formulation of quantum error correction:
-
David Kribs, Raymond Laflamme, David Poulin, A Unified and Generalized Approach to Quantum Error Correction, Phys. Rev. Lett. 94, 180501 (2005) (arXiv:quant-ph/0412076)
-
David W. Kribs, Raymond Laflamme, David Poulin, Maia Lesosky, Operator quantum error correction, Quant. Inf. & Comp., 6 (2006), 383-399 (arXiv:quant-ph/0504189)
-
Cédric Bény, Achim Kempf, David W. Kribs, Generalization of Quantum Error Correction via the Heisenberg Picture, Phys. Rev. Lett. 98, 100502 – Published 7 March 2007 (doi:10.1103/PhysRevLett.98.100502, arXiv:quant-ph/0608071)
-
Cédric Bény, Achim Kempf, David W. Kribs, Quantum Error Correction of Observables, Phys. Rev. A 76, 042303 (2007) (arXiv:0705.1574)
Introduction and survey:
-
Alexei Kitaev, Quantum computations: algorithms and error correction, Russian Mathematical Surveys, 52 6 (1997) [doi:10.1070/RM1997v052n06ABEH002155, pdf]
-
Michael A. Nielsen, Isaac L. Chuang, Chapter 10 of: Quantum computation and quantum information, Cambridge University Press (2000) [doi:10.1017/CBO9780511976667, pdf, pdf]
-
Simeon Ball, Aina Centelles, Felix Huber, Quantum error-correcting codes and their geometries (arXiv:2007.05992)
-
Andrew M. Steane, A Tutorial on Quantum Error Correction, in: Proceedings of the International School of Physics “Enrico Fermi”, course CLXII, “Quantum Computers, Algorithms and Chaos” (2006) [pdf, pdf]
-
Daniel Gottesman: An Introduction to Quantum Error Correction and Fault-Tolerant Quantum Computation, in: Quantum Information Science and Its Contributions to Mathematics, Proceedings of Symposia in Applied Mathematics 68 (2010) [arXiv:0904.2557, doi:10.1090/psapm/068]
-
Isaac L. Chuang, Quantum error correction, Chapter 7 in: Quantum Machines: Measurement and Control of Engineered Quantum Systems Lecture Notes of the Les Houches Summer School 96 (2011) 273–320 [doi:10.1093/acprof:oso/9780199681181.003.0007]
-
Simon J. Devitt, Kae Nemoto, William J. Munro, Quantum Error Correction for Beginners, Rep. Prog. Phys. 76 (2013) 076001 [arXiv:0905.2794, doi:10.1088/0034-4885/76/7/076001]
-
Daniel A. Lidar, Todd A. Brun (eds.): Quantum Error Correction, Cambridge University Press (2013) [ISBN:9780521897877, doi:10.1017/CBO9781139034807]
-
Héctor Bombín: An Introduction to Topological Quantum Codes, in: Quantum Error Correction, Cambridge University Press (2013) [ISBN:9780521897877, arxiv:1311.0277]
-
Eric Rowell, Zhenghan Wang, Section 3.2.3 of: Mathematics of Topological Quantum Computing, Bull. Amer. Math. Soc. 55 (2018), 183-238 (arXiv:1705.06206, doi:10.1090/bull/1605)
-
Scott Aaronson, Chapter 27 of: Introduction to Quantum Information Science (2018) [pdf, webpage]
-
Joschka Roffe, Quantum Error Correction: An Introductory Guide, Contemporary Physics 2019 (arXiv:1907.11157)
-
Bei Zeng, Xie Chen, Duan-Lu Zhou, Xiao-Gang Wen:
Sec. 3 of: Quantum Information Meets Quantum Matter – From Quantum Entanglement to Topological Phases of Many-Body Systems, Quantum Science and Technology (QST), Springer (2019) arXiv:1508.02595, doi:10.1007/978-1-4939-9084-9
-
Guanyu Zhu, Andrew Cross, Hardware-aware approach for fault-tolerant quantum computation, IBM Research Blog, September 2, 2020
-
Priya J. Nadkarni, Narayanan Rengaswamy, Bane Vasić: Tutorial on Quantum Error Correction for 2024 Quantum Information Knowledge (QuIK) Workshop [arXiv:2407.12737, inSpire:2808724]
See also:
-
Wikipedia, Quantum error correction
In the context of quantum secret sharing:
- Richard Cleve, Daniel Gottesman, Hoi-Kwong Lo, How to share a quantum secret, Phys. Rev. Lett. 83 (1999) 648-651 (arXiv:quant-ph/9901025)
In the context of quantum communication:
- Matthias Christandl, Alexander Müller-Hermes, Fault-tolerant Coding for Quantum Communication,
IEEE Transactions on Information Theory, [arXiv:2009.07161 doi:10.1109/TIT.2022.3169438]
On (in-)compatibility of quantum error correction with universality of quantum gates (Eastin-Knill theorem):
-
Bryan Eastin, Emanuel Knill, Restrictions on Transversal Encoded Quantum Gate Sets, Phys. Rev. Lett. 102, 110502 (2009) (arXiv:0811.4262)
-
Paul Webster, Michael Vasmer, Thomas R. Scruby, Stephen D. Bartlett, Universal Fault-Tolerant Quantum Computing with Stabiliser Codes (arXiv:2012.05260)
For quantum annealing processes:
- Kristen L. Pudenz, Tameem Albash, Daniel A. Lidar: Error-corrected quantum annealing with hundreds of qubits, Nature Communications 5 3243 (2014) [doi:10.1038/ncomms4243]
On continuous variable quantum codes:
-
Samuel L. Braunstein, Peter van Loock, §IV.C in: Quantum information with continuous variables, Rev. Mod. Phys. 77 2 (2005) 513 [arXiv:quant-ph/0410100, doi:10.1103/RevModPhys.77.513]
-
Samuel L. Braunstein, Arun K. Pati, Quantum Information with Continuous Variables, Springer (2003) [doi:10.1007/978-94-015-1258-9]
-
Allan D. C. Tosta, Thiago O. Maciel, Leandro Aolita, Grand Unification of continuous-variable codes [arXiv:2206.01751]
In relation to the SYK model:
- Shao-Kai Jian, Chunxiao Liu, Xiao Chen, Brian Swingle, Pengfei Zhang, Quantum error as an emergent magnetic field (arXiv:2106.09635)
In relation to continuous symmetries:
- Zi-Wen Liu, Sisi Zhou, Approximate symmetries and quantum error correction (arXiv:2111.06355)
Further developments:
- Mackenzie H. Shaw, Andrew C. Doherty, Arne L. Grimsmo, Stabilizer subsystem decompositions for single- and multi-mode Gottesman-Kitaev-Preskill codes [arXiv:2210.14919]
On relevant classical control mechanisms:
-
Hideo Mabuchi, Continuous quantum error correction as classical hybrid control, New J. Phys. 11 (2009) 105044 [doi:10.1088/1367-2630/11/10/105030]
-
Alexandru Paler, Daniel Herr, Simon J. Devitt, Really Small Shoe Boxes - On Realistic Quantum Resource Estimation, Computer 52 6 (2019) [arXiv:1902.08104, doi:10.1109/MC.2019.2908621]
In relation to the Penrose tiling:
- Zhi Li, Latham Boyle, The Penrose Tiling is a Quantum Error-Correcting Code [arXiv:2311.13040]
Relating quantum error correction to linear logic:
- Daniel Murfet, William Troiani, Linear Logic and Quantum Error Correcting Codes [arXiv:2405.19051]
Experimental realization
Realization of quantum error correction in experiment, hence in actual quantum computers:
-
D. G. Cory, M. D. Price, W. Maas, Emanuel Knill, Raymond Laflamme, Wojchiek H. Zurek, T. F. Havel, and S. S. Somaroo, Experimental Quantum Error Correction, Phys. Rev. Lett. 81, 2152 (1998) (doi:10.1103/PhysRevLett.81.2152)
-
Daniel Nigg, Markus Mueller, Esteban A. Martinez, Philipp Schindler, Markus Hennrich, Thomas Monz, Miguel A. Martin-Delgado, Rainer Blatt,
Experimental Quantum Computations on a Topologically Encoded Qubit, Science 18 Jul 2014: Vol. 345, Issue 6194, pp. 302-305 (arXiv:1403.5426, doi:10.1126/science.1253742)
(via methods from topological quantum computation)
-
Adrian Cho, The biggest flipping challenge in quantum computing, Science News Jul. 9, 2020
(exposition)
-
Y. Ma et al. Error-transparent operations on a logical qubit protected by quantum error correction, Nature Physics volume 16, pages 827–831 (2020) (doi:10.1038/s41567-020-0893-x)
-
Ming Gong et al. Experimental exploration of five-qubit quantum error correcting code with superconducting qubits, National Science Review, nwab011 (2021) (doi:10.1093/nsr/nwab011)
survey in:
EurekaAlert, Science China Press: Demonstration of the universal quantum error correcting code with superconducting qubits, March 2021 (2021-03/scp-dot031521)
-
Erik Lucero (Google), Unveiling our new Quantum AI campus, May 18, 2021
(outlook)
-
Th. Monz et al., Demonstration of fault-tolerant universal quantum gate operations, Nature 605 (2022) 675–680 [doi:10.1038/s41586-022-04721-1]
-
Markus Müller, Andreas Wallraff et al., Realizing Repeated Quantum Error Correction in a Distance-Three Surface Code, Nature 605 (2022) 669–674 [arXiv:2112.03708, doi:10.1038/s41586-022-04566-8]
-
Markus Müller et al., Demonstration of fault-tolerant universal quantum gate operations, Nature 605 (2022) 675-680 [doi:10.1038/s41586-022-04721-1, arXiv:2111.12654]
Via holographic tensor networks
First quantum error correcting codes associated with planar bulk/boundary systems:
-
S. B. Bravyi, Alexei Kitaev, Quantum codes on a lattice with boundary (arXiv:quant-ph/9811052)
-
Michael Freedman, David A. Meyer, Projective Plane and Planar Quantum Codes, Found. Comput. Math. 1, 325–332 (2001) (arXiv:quant-ph/9810055, doi:10.1007/s102080010013)
First suggestion relating quantum error correction to black hole entropy:
- Erik Verlinde, Herman Verlinde, Black Hole Entanglement and Quantum Error Correction, J. High Energ. Phys. 2013, 107 (2013) (arXiv:1211.6913, doi:10.1007/JHEP10(2013)107)
Introducing the idea of quantum error correcting codes given by tensor network states:
-
Andrew J. Ferris, David Poulin, Tensor Networks and Quantum Error Correction, Phys. Rev. Lett. 113, 030501 (2014) (arXiv:1312.4578)
-
Dave Bacon, Steven T. Flammia, Aram W. Harrow, Jonathan Shi, Sparse Quantum Codes from Quantum Circuits, Proc. of STOC ‘15, pp. 327-334 (2015); IEEE Transactions on Information Theory, vol 63, no 4, pp 2464-2479, April 2017 (arXiv:1411.3334)
following observations in
-
Brian Swingle, Entanglement Renormalization and Holography, Phys. Rev. D 86, 065007 (2012) (arXiv:0905.1317)
-
Brian Swingle, Constructing holographic spacetimes using entanglement renormalization (arXiv:1209.3304, spire:1185813)
Interpretation of holographic tensor networks encoding holographic entanglement entropy in models for AdS2-CFT1 duality as quantum error correcting codes:
-
Ahmed Almheiri, Xi Dong, Daniel Harlow, Bulk Locality and Quantum Error Correction in AdS/CFT, JHEP 1504:163,2015 (arXiv:1411.7041, doi:10.1007/JHEP04(2015)163)
(using Bény-Kempf-Kribs 06)
with precursor observations in
-
Beni Yoshida, Information storage capacity of discrete spin systems, Annals of Physics 338, 134 (2013) (arXiv:1111.3275)
(focus on classical error correcting codes)
-
Jose I. Latorre, German Sierra, Holographic codes (arXiv:1502.06618)
and concrete implementation by the HaPPY code:
- Fernando Pastawski, Beni Yoshida, Daniel Harlow, John Preskill, Holographic quantum error-correcting codes: Toy models for the bulk/boundary correspondence, JHEP 06 (2015) 149 (arXiv:1503.06237)
and possibly more generally:
- Daniel Harlow, The Ryu–Takayanagi Formula from Quantum Error Correction, Comm. Math. Phys. 354 (2017) 865–912 [doi:10.1007/s00220-017-2904-z, arXiv:1607.03901]
Introduction of the more general Majorana dimer code:
- Alexander Jahn, Marek Gluza, Fernando Pastawski, Jens Eisert, Majorana dimers and holographic quantum error-correcting codes, Phys. Rev. Research 1, 033079 (2019) (arXiv:1905.03268)
Exposition and review:
-
John Preskill, Is spacetime a quantum error-correcting code?, talk at KITP 2015 (pdf, pdf)
-
Daniel Harlow, TASI Lectures on the Emergence of Bulk Physics in AdS/CFT, PoS TASI2017 (2018) 002 (arXiv:1802.01040, doi:10.22323/1.305.0002)
-
Pratik Rath, Aspects of Holography And Quantum Error Correction, 2020 (pdf, pdf)
-
Melanie Swan, Renato P dos Santos, Frank Witte, The AdS/CFT Correspondence and Holographic Codes (doi:10.1142/9781786348210_0013, doi:10.1142/9781786348210_0014), Part 5 in: Between Science and Economics, Volume 2: Quantum Computing Physics, Blockchains, and Deep Learning Smart Networks, World Scientific 2020 (doi:10.1142/q0243)
-
Daniel Harlow, Computation and Holography, talk at Snowmass Computational Frontier Workshop 2020 (pdf, pdf)
-
Alexander Jahn, Jens Eisert, Holographic tensor network models and quantum error correction: A topical review (arXiv:2102.02619)
-
Tanay Kibe, Prabha Mandayam, Ayan Mukhopadhyay, Holographic spacetime, black holes and quantum error correcting codes: A review (arXiv:2110.14669)
Further discussion of holographic quantum error correcting codes:
-
Henrique Lazari, Reginaldo Palazzo Jr., Geometrically uniform hyperbolic codes, Comput. Appl. Math. vol.24 no.2 Petrópolis 2005 (doi:10.1590/S0101-82052005000200002)
-
Enrico M. Brehm, Benedikt Richter, Classical Holographic Codes, Phys. Rev. D 96, 066005 (2017) (arXiv:1609.03560)
-
Fernando Pastawski, John Preskill, Code properties from holographic geometries, Phys. Rev. X 7, 021022 (2017) (arXiv:1612.00017)
-
Robert J. Harris, Nathan A. McMahon, Gavin K. Brennen, Thomas M. Stace, Calderbank-Steane-Shor Holographic Quantum Error Correcting Codes, Phys. Rev. A 98, 052301 (2018) (arXiv:1806.06472)
-
Tamara Kohler, Toby Cubitt, Toy Models of Holographic Duality between local Hamiltonians, J. High Energy Phys. 2019:17 (2019) (arXiv:1810.08992)
-
Tobias J. Osborne, Deniz E. Stiegemann, Dynamics for holographic codes, J. High Energ. Phys. 2020, 154 (2020) (arXiv:1706.08823)
-
Martina Gschwendtner, Robert König, Burak Şahinoğlu & Eugene Tang, Quantum error-detection at low energies, Journal of High Energy Physics volume 2019, Article number: 21 (2019) (arXiv:1902.02115)
-
Nathan A. McMahon, Gavin K. Brennen, Thomas M. Stace, Robert J. Harris, Elliot Coupe, Decoding Holographic Codes with an Integer Optimisation Decoder (arXiv:2008.10206)
-
Terry Farrelly, Robert J. Harris, Nathan A. McMahon, Thomas M. Stace, Tensor-network codes (arXiv:2009.10329)
-
ChunJun Cao, Brad Lackey, Approximate Bacon-Shor Code and Holography (arXiv:2010.05960)
-
Sam Cree, Kfir Dolev, Vladimir Calvera, Dominic J. Williamson, Fault-tolerant logical gates in holographic stabilizer codes are severely restricted (arXiv:2103.13404)
-
Robert de Mello Koch, Eunice Gandote, Nirina Hasina Tahiridimbisoa, Hendrik J.R. Van Zyl, Quantum Error Correction and Holographic Information from Bilocal Holography (arXiv:2106.00349)
-
Chris Akers, Geoff Penington, Quantum minimal surfaces from quantum error correction (arXiv:2109.14618)
-
ChunJun Cao, Brad Lackey, Quantum Lego: Building Quantum Error Correction Codes from Tensor Networks, PRX Quantum 3 020332 (2022) arXiv:2109.08158, doi:10.1103/PRXQuantum.3.020332
-
Jason Pollack, Patrick Rall, Andrea Rocchetto, Understanding holographic error correction via unique algebras and atomic examples, Journal of High Energy Physics, 56 (2022) arXiv:2110.14691
-
Dmitry S. Ageev, Exploring uberholography [arXiv:2208.07387]
-
Matthew Steinberg, Sebastian Feld, Alexander Jahn, Holographic Codes from Hyperinvariant Tensor Networks [arXiv:2304.02732]
Understanding in terms of the eigenstate thermalization hypothesis:
- Ning Bao, Newton Cheng, Eigenstate Thermalization Hypothesis and Approximate Quantum Error Correction, JHEP 08 (2019) 152 (arXiv:1906.03669)
In relation to holographic Renyi entropy:
- Chris Akers, Pratik Rath, Holographic Renyi entropy from quantum error correction, J. High Energ. Phys. 2019, 52 (2019) (arXiv:1811.05171)
From tesselations of higher-dimensional hyperbolic space:
- Vivien Londe, Anthony Leverrier, Golden codes: quantum LDPC codes built from regular tessellations of hyperbolic 4-manifolds (arXiv:1712.08578)
In view of black hole thermodynamics:
-
Ahmed Almheiri, Holographic Quantum Error Correction and the Projected Black Hole Interior (arXiv:1810.02055)
-
Isaac H. Kim, Eugene Tang, John Preskill, The ghost in the radiation: Robust encodings of the black hole interior, JHEP 2020, 31 (2020) (arXiv:2003.05451)
-
Chris Akers, Netta Engelhardt, Daniel Harlow, Geoff Penington, Shreya Vardhan, The black hole interior from non-isometric codes and complexity [arXiv:2207.06536]
-
Daniel Harlow, A theory of the black hole interior, talk at Strings 2022 [indico:4940817/]
Discussion of gauge symmetry of holographic tensor networks and their quantum error correcting codes:
- Kfir Dolev, Vladimir Calvera, Sam Cree, Dominic J. Williamson, Gauging the bulk: generalized gauging maps and holographic codes (arXiv:2108.11402)
Relation of quantum error correcting codes to the Monster vertex operator algebra and more generally to 2d SCFT and string theory:
- Jeffrey A. Harvey, Gregory W. Moore, Moonshine, Superconformal Symmetry, and Quantum Error Correction, J. High Energ. Phys. 2020, 146 (2020). (arXiv:2003.13700)
In relation to the large N limit:
- Alexey Milekhin, Quantum error correction and large (arXiv:2008.12869)
In relation to renormalization group flow:
- Keiichiro Furuya, Nima Lashkari, Mudassir Moosa, Renormalization group and approximate error correction (arXiv:2112.05099)
In relation to fixed-point path integrals:
- Andreas Bauer, Topological error correcting processes from fixed-point path integrals (arXiv:2303.16405)
Musings on possible implications on relations between quantum gravity and quantum information:
-
Simons Foundation, It from Qubit: Simons Collaboration on Quantum Fields, Gravity and Information
-
Iulia Georgescu, Strings and qubits, Nature Reviews Physics volume 1, page 477 (2019) (doi:s42254-019-0087-6)
-
Natalie Wolchover, How Space and Time Could Be a Quantum Error-Correcting Code, Quanta Magazine, Jan. 3 2019
-
Tom Banks, Holographic Space-time and Quantum Information (arXiv:2001.08205)
-
ChunJun Cao, From Quantum Codes to Gravity: A Journey of Gravitizing Quantum Mechanics (arXiv:2112.00199)
-
Takaaki Kuwahara, Ryota Nasu, Gota Tanaka, Asato Tsuchiya: Quantum error correction realized by the renormalization group in scalar field theories [arXiv:2401.17795]
Last revised on March 3, 2025 at 15:59:05. See the history of this page for a list of all contributions to it.