nLab Born rule

Idea

The Born rule is the core statement of coordination in the foundations of quantum physics:

In its version for pure states the Born rule says that

• for $A$ an observable in the form of a Hermitean operator on the given Hilbert space $\mathcal{H}$ of pure quantum states with Hermitian inner product $\langle\text{-}\vert\text{-}\rangle$

• $P$ denoting the projection operator on a given eigenstate of this operator,

• $\pi \,\in\, \mathcal{H}$ a pure state;

then the probability of observing the given eigenstate in a quantum system which is in state $\psi$ equals (in bra-ket notation):

$$\frac{ \langle \psi \vert P \vert \psi \rangle }{ \langle \psi \vert \psi \rangle } \,.$$

In particular, if $W$ is an orthonormal basis for the Hilbert space of states associated with a quantum measurement-procedure, then the probability of measuring the result $w$ on a system in state $\left\vert \psi \right\rangle$ is

$$\frac{ \langle \psi \vert w \rangle \langle w \vert \psi \rangle }{ \langle \psi \vert \psi \rangle } \;\;=\;\; \frac{ \big\vert \langle w \vert \psi \rangle \big\vert^2 }{ \langle \psi \vert \psi \rangle }$$

and so if the state is normalized to begin with ($\langle \psi \vert \psi \rangle$ = 1 ), then the probability is

$$P_\psi(w) \;=\; \big\vert \langle w \vert \psi \rangle \big\vert^2 \,.$$

Essentially in this form the rule was first formulated by Born 1926b p 805.

Related concepts

• quantum probability

quantum probability theory – observables and states

• states

  • classical state

  • quantum state

    • space of states (in geometric quantization)

    • state on a star-algebra, quasi-state

    • qbit, Bell state

      dimer, tensor network state

    • quantum state preparation

    • probability amplitude, quantum fluctuation

    • pure state

      • wave function

      • bra-ket

      • Bell state

    • quantum superposition, quantum interference

    • quantum entanglement

    • quantum measurement

      wave function collapse

      Born rule

      deferred measurement principle

      quantum reader monad

      measurement problem

    • superselection sector

    • mixed state, density matrix

      entanglement entropy

      holographic entanglement entropy

    • coherent quantum state

  • ground state, excited state

  • quasi-free state

  • Fock space, second quantization

  • vacuum, vacuum state

    • Hadamard state

    • vacuum diagram

    • vacuum expectation value, vacuum amplitude, vacuum fluctuation

    • vacuum energy

    • vacuum polarization

    • interacting vacuum

    • thermal vacuum, KMS state

    • vacuum stability

      • false vacuum, tachyon, Coleman-De Luccia instanton

    • theta vacuum

    • perturbative string theory vacuum

      • non-geometric string theory vacuum

      • landscape of string theory vacua

  • entangled state

  • tensor network state

    • matrix product state

    • tree tensor network state

• observables

  • quantum observable, beable

  • algebra of observables, star-algebra

  • Bohr topos

  • quantum operator (in geometric quantization)

  • quantum operation, quantum effect, effect algebra

  • in quantum field theory

    • local observable

    • polynomial observable

      • linear observable

        • field observable

    • regular observable

    • microcausal observable

    • normal-ordered product, time-ordered products, retarded product

    • Wick algebra

    • scattering amplitude

    • interacting field algebra of observables, Bogoliubov's formula

• GNS construction

• theorems

  • order-theoretic structure in quantum mechanics

    • Gleason's theorem

    • Alfsen-Shultz theorem

    • Harding-Döring-Hamhalter theorem

    • Kochen-Specker theorem

    • Nuiten's lemma

  • Wigner's theorem

  • no-cloning theorem

  • Bell's theorem

References

Historical origins

The Born rule is named in honor of

• Max Born, Zur Quantenmechanik der Stoßvorgänge, Zeitschrift für Physik 37 (1926) 863–867 [doi:10.1007/BF01397477]

where it appears (though disregarding the norm symbol) as a brief footnote-added-in-proof:

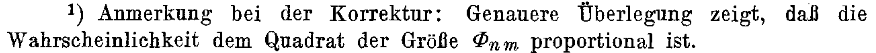
and its expanded version

• Max Born, Quantenmechanik der Stoßvorgänge, Zeitschrift für Physik 38 (1926) 803–827 [doi:10.1007/BF01397184]

which provides the mathematical details (p. 805):

and finally in the followup

• Max Born, Das Adiabatenprinzip in der Quantenmechanik, Zeitschrift für Physik 40 (1927) 167–192 [doi:10.1007/BF01400360]

which makes the interpretation more explicit (p. 171):

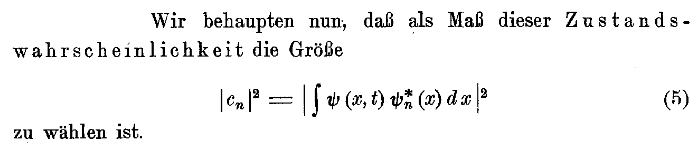
The generalization of this idea to probability densities for continuous observables is due to Wolfgang Pauli, as first recounted in:

• Pascual Jordan, Über eine neue Begründung der Quantenmechanik, Zeitschrift für Physik 40 (1927) 809–838 [doi:10.1007/BF01390903]

and then by Pauli himself, again in a footnote:

• Wolfgang Pauli, Über Gasentartung und Paramagnetismus, Zeitschrift für Physik: A Hadrons and nuclei 41 (1927) 81–102 [doi:10.1007/BF01391920]

Early review of the Born-Pauli rule:

• David Hilbert, John von Neumann, Lothar W. Nordheim, Über die Grundlagen der Quantenmechanik, Math. Ann. 98 (1928) 1–30 [doi:10.1007/BF01451579]

where it is once again a footnote:

and in

• Paul A. M. Dirac, The physical interpretation of the quantum dynamics, Proceedings of the Royal Society of London 113 765 (1927) [doi:10.1098/rspa.1927.0012]

The full recognition and amplification of the Born rule as a pillar of quantum physics making it a probabilistic theory (cf. quantum probability) is (maybe besides Jordan 1927) due to:

• John von Neumann, Die quantenmechanische Statistik, Part III in:

  Mathematische Grundlagen der Quantenmechanik, Springer (1932, 1971) [doi:10.1007/978-3-642-96048-2]

  Mathematical Foundations of Quantum Mechanics Princeton University Press (1955) [doi:10.1515/9781400889921, Wikipedia entry]

Historical survey:

• Jagdish Mehra, Helmut Rechenberg, The Probability Interpretation and the Statistical Transformation Theory, the Physical Interpretation, and the Empirical and Mathematical Foundations of Quantum Mechanics 1926-1932, Part 1 in: The Historical Development of Quantum Theory. Volume 6: The Completion of Quantum Mechanics, 1926-1941, Springer (2001) [ISBN:978-0-387-98971-6]

Further discussion

Review:

• Klaas Landsman, The Born rule and its interpretation, in: Compendium of Quantum Physics, Springer (2009) 64-70 [doi:10.1007/978-3-540-70626-7_20, pdf, pdf]

• Arnold Neumaier: The Born rule – 100 years ago and today [arXiv:2502.08545]

See also:

• Wikipedia, Born rule