nLab quantum teleportation
Context
Quantum systems
-
quantum algorithms:
Contents
Idea
What has been called quantum “teleportation” (BBCJPW 1993) is a procedure (a “protocol”) in quantum information theory by which the exact transmission of a quantum state (such as that of some qbits) is equivalently established by the transmission of classical information, provided that sender and receiver “share a Bell state”, hence that each have access to one half of a pair of subsystems which have been prepared in a maximally entangled quantum state with each other. The protocol involves a quantum measurement and its ensuing wavefunction collapse destroys (“uses up”) this entangled state in order to transmit the remaining quantum state – which somewhat relativizes the imagery of “teleportation”.
While this prose may appear somewhat exotic, the actual mathematics underlying the “quantum teleportation protocol” is an elementary and direct consequence of the most basic axioms of quantum mechanics (in fact it is all but a self-evident consequence when formulated in modern notation, see below). What makes quantum teleportation interesting is the (quantum) information theoretic perspective on it.
History and perspective
Given that the basic axioms of quantum physics were established in the 1920s and widely appreciated by the 1930s, the observation of the possibility of “quantum teleportation” only in 1993, using tools and notation available to the founding fathers, may make one wonder (e.g Coecke 2010, p. 1):
why did it take us 60 years to discover the conceptually intriguing and easily derivable physical phenomenon of ‘quantum teleportation’?
Traditional reviews of the matter maintain that the phenomenon just happens to be intrinsically tricky to see through – e.g. Aaronson 2018, p. 71, apparently in reply to his student’s puzzlement “How do people come up with this stuff?”, asserts that:
These sorts of protocols can be hard to find.
On the other hand, it was observed around Coecke 2004, Abramsky & Coecke 2004 – and pronouncedly brought out in Coecke 2005, 2010 – that the logical structure of quantum information theory in general and that of quantum teleportation in particular is transparently captured by string diagram-calculus for the ambient compact closed tensor category of finite dimensional Hilbert spaces (see finite quantum mechanics in terms of dagger-compact categories):
In this category-theoretic language, the quantum teleportation protocol is essentially just the zig-zag identity for dualizable objects (here: finite-dimensional Hilbert spaces) in any monoidal category, see below.
This suggests the following alternative answer, from Coecke 2005, p. 1:
Why did discovering quantum teleportation take 60 year?
We claim that this is due to a ‘bad quantum formalism’ (bad wrong) and this badness is in particular due to the fact that the formalism is ‘too low level’.
Here “bad quantum formalism” refers to the traditional notation as in the original BBCJPW93 and in traditional reviews (e.g. Aaronson 2018, see also Coecke 05 ftn. 5 on p. 8), while the suggested high-level improvement is string diagram-calculus for the ambient tensor category of finite-dimensional Hilbert spaces, further discussed at finite quantum mechanics in terms of dagger-compact categories.
Statement
The quantum teleportation protocol is neatly expressed in string diagram-calculus as follows (essentially following Coecke 2005):
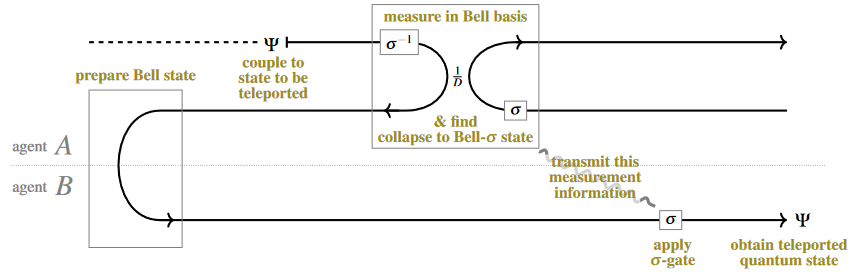
Here, by the general laws of string diagrams: a solid line pointing to the right represents a given finite dimensional Hilbert space (of dimension ), the same line pointing backwards denotes its dual vector space, two lines running parallel reflects the tensor product of the corresponding Hilbert spaces, and the curve “” denotes evaluation .
The wiggly line denotes a classically controlled quantum gate, controlled by the quantum measurement-outcome which is reflected by the projection operator shown at the top.
That – for any fixed measurement outcome at the top with the correspondingly controlled correction gate operation at the bottom – this string diagram (represents a linear map which) takes the quantum state from “Agent A” (“Alice”) to the same state for “Agent B” (“Bob”), as shown is immediate from the zig-zag identity, hence from the fact that the curved line may be “yanked straight” to an identity line, without changing the operational value of the diagram. This is the transparent proof of the quantum teleporation protocol.
Notice that this is a rigorous proof, and yet this string diagram is close to informal flow-charts traditionally used to illustrate the idea of quantum teleportation (e.g Bouwmeester, Ekert & Zeilinger 2020, Fig. 3.1).
In more detail, here the top box shows the projector onto a Bell state with one variable transformed by a unitary operator . This reflects the (random/unpredictable!) result of a quantum measurement in a corresponding linear basis for (according to the collapse postulate).
Concretely, if the Hilbert space represented by a single solid line is that of a single qbit, i.e. if (), then may be taken to range over the unitary Pauli matrices:
In this case, the component-evaluation of the above diagram yields the quantum teleportation protocol in its traditional form (due to BBCJPW93) which is the following quantum circuit (cf. GLRSV13, p. 5) on qbits (where “” denotes the Hadamard gate, the circles denote the quantum CNOT gates and the boxed pointers denote quantum measurement in the qbit-basis):

The concrete implementation of the above protocol on given quantum hardware will look more complicated.
For instance, the implementation of the quantum teleportation protocol as a circuit of braid gates of Ising anyons (topological quantum computation) is given in Xu & Zhou 2022:
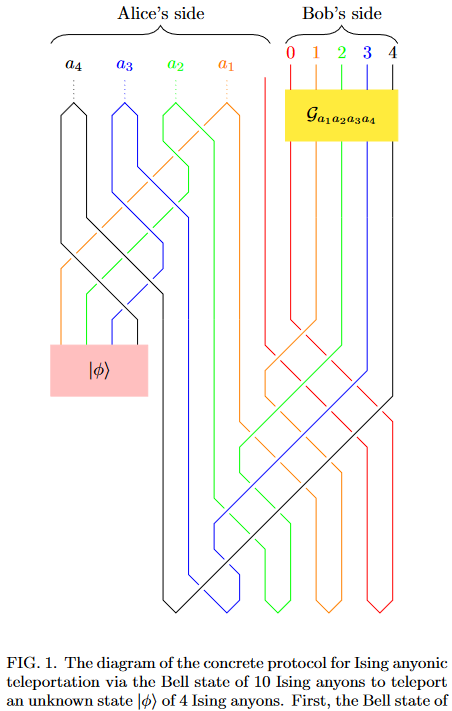
See also Valera (2023).
Related concepts
References
The original article:
- Charles H. Bennett, Gilles Brassard, Claude Crépeau, Richard Jozsa, Asher Peres, William K. Wootters: Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels, Phys. Rev. Lett. 70 1895 (1993) [doi:10.1103/PhysRevLett.70.1895]
Traditional review:
-
Michael A. Nielsen, Isaac L. Chuang, §1.3.7 in: Quantum computation and quantum information, Cambridge University Press (2000) [doi:10.1017/CBO9780511976667, pdf, pdf]
-
Scott Aaronson, §10.1 in Introduction to Quantum Information Science (2018) [pdf, webpage]
and phrased in the quantum programming language Quipper:
- Alexander Green, Peter LeFanu Lumsdaine, Neil Ross, Peter Selinger, Benoît Valiron, p. 5 of:
An Introduction to Quantum Programming in Quipper, Lecture Notes in Computer Science 7948:110-124, Springer, 2013 (arXiv:1304.5485)
and with focus on the experimental realization:
- Dirk Bouwmeester, Artur Ekert, Anton Zeilinger (eds.), §3.3 of: The Physics of Quantum Information – Quantum Cryptography, Quantum Teleportation, Quantum Computation, Springer (2020) [doi:10.1007/978-3-662-04209-0]
See also:
- Wikipedia, Quantum teleportation
Discussion via string diagram-calculus (finite quantum mechanics in terms of dagger-compact categories):
-
Bob Coecke, §4 of: The logic of entanglement, in: Horizons of the Mind. A Tribute to Prakash Panangaden, Lecture Notes in Computer Science 8464 (2014) [arXiv:quant-ph/0402014, doi:10.1007/978-3-319-06880-0_13]
-
Samson Abramsky, Bob Coecke, §2 in: A categorical semantics of quantum protocols, Proceedings of the 19th IEEE conference on Logic in Computer Science (LiCS’04). IEEE Computer Science Press (2004) [arXiv:quant-ph/0402130, doi:10.1109/LICS.2004.1319636]
-
Bob Coecke, §3c in: Kindergarten Quantum Mechanics, in Quantum Theory: Reconsideration of Foundations (QTRF 3) Vaxjo, Sweden, June 6-11, 2005, AIP Conf. Proc. 810 (2006) [arXiv:quant-ph/0510032, doi:10.1063/1.2158713]
-
Bob Coecke, Quantum Picturalism, Contemporary Physics 51 (2010) 59-83 [arXiv:0908.1787, doi:10.1080/00107510903257624]
Realization in experiment:
-
Dirk Bouwmeester, Jian-Wei Pan, Klaus Mattle, Manfred Eibl, Harald Weinfurter, Anton Zeilinger, Experimental quantum teleportation, Nature 390 575–579 (1997) [doi:10.1038/37539]
-
Syed Tahir Amin, Aeysha Khalique, Practical Quantum Teleportation of an Unknown Quantum State, Can. J. Phys. 95 5 (2017) 498 [arXiv:1508.01141, doi:10.1139/cjp-2016-0758]
-
Dario Lago-Rivera, Jelena V. Rakonjac, Samuele Grandi, Hugues de Riedmatten, Long-distance multiplexed quantum teleportation from a telecom photon to a solid-state qubit [arXiv:2209.06249]
Implementation of the quantum teleportation protocol in topological quantum computation via braiding of Ising anyons:
- Cheng-Qian Xu, D. L. Zhou, Quantum teleportation using Ising anyons, Phys. Rev. A 106 012413 (2022) [arXiv:2201.11923, doi:10.1103/PhysRevA.106.012413]
and via fusion of anyons:
- Sachin J. Valera, Topological Quantum Teleportation and Superdense Coding Without Braiding [arXiv:2303.17700]
Implementation in quantum programming languages:
Argument that the image of quantum teleportation under AdS-CFT duality is wormhole traversal (see also at ER = EPR):
-
Erik Verlinde, Herman Verlinde, A Conversation on ER = EPR [arXiv:2212.09389]
-
Ping Gao, Daniel Louis Jafferis, Aron C. Wall, Traversable Wormholes via a Double Trace Deformation, Journal of High Energy Physics 2017 151 (2017) [arXiv:1608.05687, doi:10.1007/JHEP12(2017)151]
-
Juan Maldacena, Douglas Stanford, Zhenbin Yang, Diving into traversable wormholes,Fortsch. Phys. 65 5 (2017) 1700034 [arXiv:1704.05333, doi:10.1002/prop.201700034]
Last revised on October 9, 2023 at 07:36:43. See the history of this page for a list of all contributions to it.