nLab tree tensor network state
Context
Monoidal categories
With braiding
With duals for objects
-
category with duals (list of them)
-
dualizable object (what they have)
-
ribbon category, a.k.a. tortile category
With duals for morphisms
With traces
Closed structure
Special sorts of products
Semisimplicity
Morphisms
Internal monoids
Examples
Theorems
In higher category theory
Quantum Field Theory
algebraic quantum field theory (perturbative, on curved spacetimes, homotopical)
Concepts
quantum mechanical system, quantum probability
interacting field quantization
Theorems
States and observables
Operator algebra
Local QFT
Perturbative QFT
Contents
Idea
What are called tree tensor network states (TTN states) in quantum physics (specifically in solid state physics and in AdS/CFT) are those tensor network states of the form of tree, often considered of fixed valence.
For example, given a metric Lie algebra (with string diagram-notation as discussed there) its Lie bracket-tensor gives rise to tree tensor network of the following form:
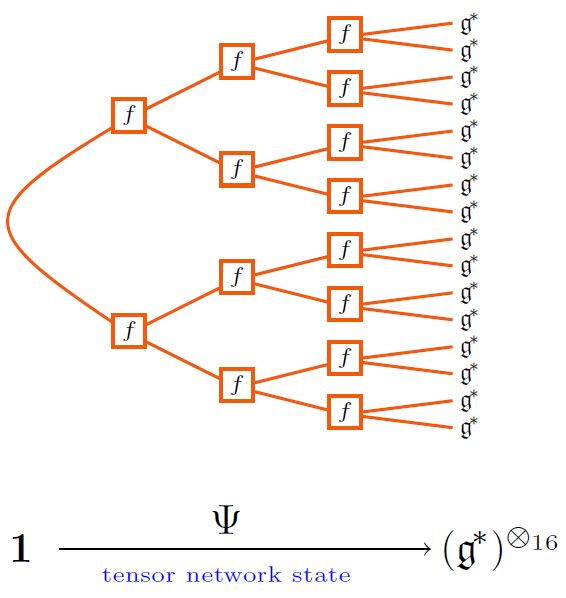
graphics from Sati-Schreiber 19c
The tree tensor network states in the form of Bruhat-Tits trees play a special role in the AdS/CFT correspondence, either as
-
a kind of lattice QFT-approximation to an actual boundary CFT quantum state,
-
as the p-adic geometric incarnation of anti de Sitter spacetime in the p-adic AdS/CFT correspondence,
-
as a reflection of actual crystal-site quantum states in AdS/CFT in solid state physics:
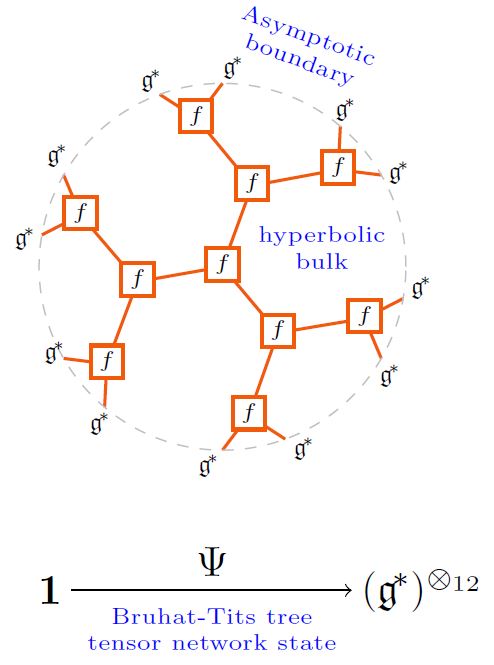
graphics from Sati-Schreiber 19c
(As in HMSS 16, HLM 19. But maybe one wants the Poincaré-dual networks, instead, as in HMPS 18?)
Related concepts
References
General
For more see the references at tensor network state.
- Shi-Ju Ran, Emanuele Tirrito, Cheng Peng, Xi Chen, Luca Tagliacozzo, Gang Su, Maciej Lewenstein, Section 2.3.3 of: Tensor Network Contractions, Lecture Notes in Physics, Springer (2020) (arXiv:1708.09213, doi:10.1007/978-3-030-34489-4)
Application to entanglement entropy
Application to entanglement entropy;
- Luca Tagliacozzo, G. Evenbly, Guifre Vidal,
Simulation of two-dimensional quantum systems using a tree tensor network that exploits the entropic area law, Phys. Rev. B 80, 235127 (2009) (arXiv:0903.5017)
Application in solid state physics
Application in solid state physics:
- Valentin Murg, Örs Legeza, Reinhard M. Noack, Frank Verstraete, Simulating Strongly Correlated Quantum Systems with Tree Tensor Networks, Phys. Rev. B 82, 205105 (2010) (arXiv:1006.3095)
Application in quantum chemistry
For application in quantum chemistry:
-
Naoki Nakatani, Garnet Kin-Lic Chan, Efficient Tree Tensor Network States (TTNS) for Quantum Chemistry: Generalizations of the Density Matrix Renormalization Group Algorithm, J. Chem. Phys. 138, 134113 (2013) (arXiv:1302.2298)
-
Klaas Gunst, Frank Verstraete, Sebastian Wouters, Örs Legeza, Dimitri Van Neck, T3NS: three-legged tree tensor network states, Chem. Theory Comput. 2018, 14, 4, 2026-2033 (arXiv:1801.09998)
-
Henrik R. Larsson, Computing vibrational eigenstates with tree tensor network states (TTNS), J. Chem. Phys. 151, 204102 (2019) (arXiv:1909.13831)
Application to -adic AdS/CFT correspondence:
Discussion of Bruhat-Tits tree-tensor networks in the context of the p-adic AdS/CFT correspondence:
-
Arpan Bhattacharyya, Ling-Yan Hung, Yang Lei, Wei Li, Tensor network and (-adic) AdS/CFT, JHEP 1801 (2018) 139 (arXiv:1703.05445)
-
Ling-Yan Hung, Wei Li, Charles M. Melby-Thompson, -adic CFT is a holographic tensor network (arXiv:1902.01411)
Application in machine learning
Application in machine learning:
-
Ding Liu, Shi-Ju Ran, Peter Wittek, Cheng Peng, Raul Blázquez García, Gang Su, Maciej Lewenstein, Machine Learning by Unitary Tensor Network of Hierarchical Tree Structure, New Journal of Physics, 21, 073059 (2019) (arXiv:1710.04833)
-
Song Cheng, Lei Wang, Tao Xiang, Pan Zhang, Tree Tensor Networks for Generative Modeling, Phys. Rev. B 99, 155131 (2019) (arXiv:1901.02217)
Last revised on February 9, 2020 at 10:42:38. See the history of this page for a list of all contributions to it.